css基础02





熟练快捷键!方便,要多练!



css复合选择器





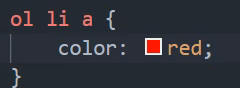


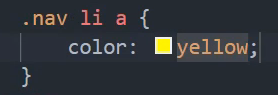

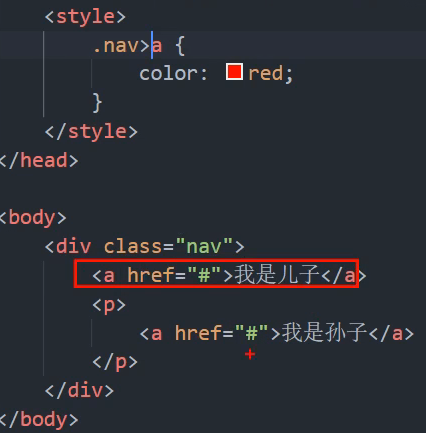
不会选孙子,有一个儿子和另一个儿子的孩子(也是孙子)同名了,但子选择器子选择儿子,同名的孙子不选。和后代选择器有一点不一样的。



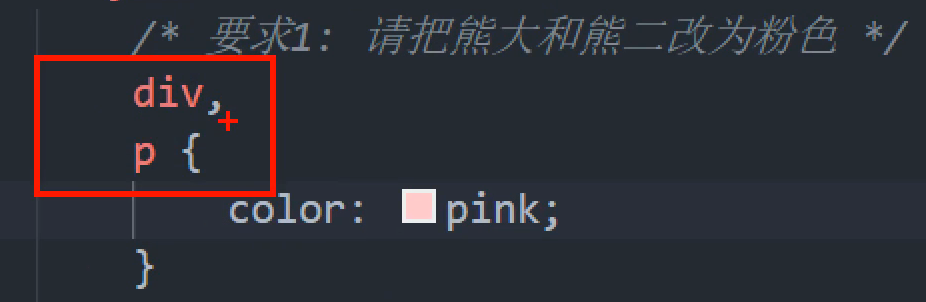
“ ,”是div和p的意思

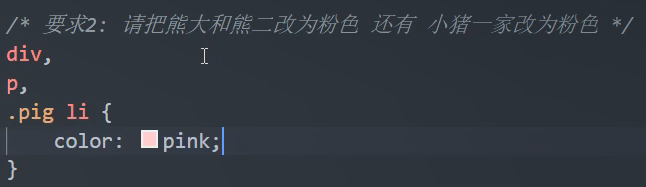


比如,将光标放在某些字上面那一行或者那几个字的底色或者字体颜色就会变化。
冒号:———代表鼠标经过的意思。



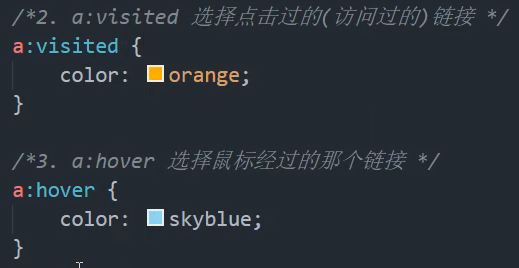
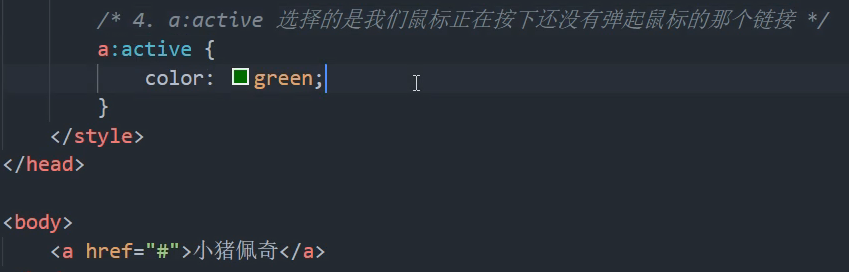
一定要按顺序书写伪链接选择器。




光标点哪里哪里就亮起来。

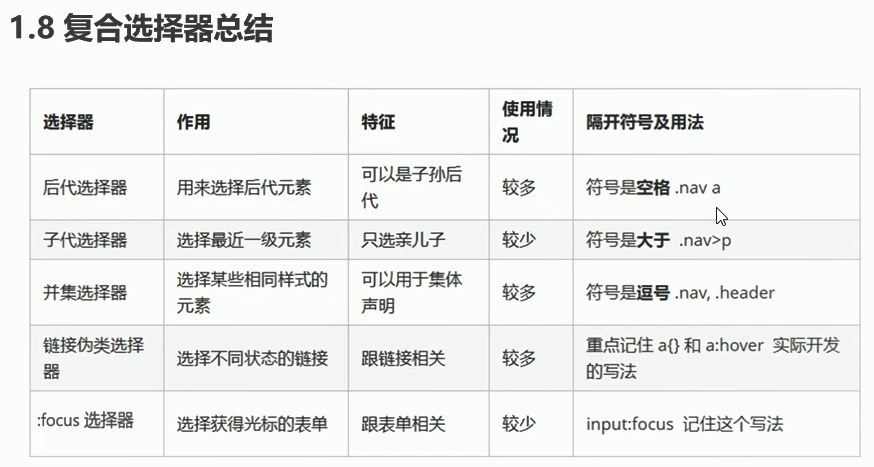

标签有很多,所以要分很多的种类。


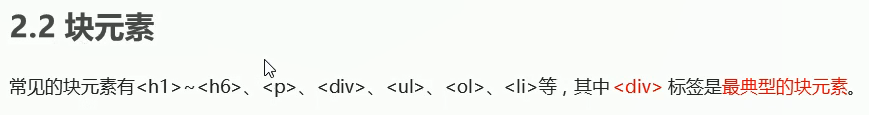

即使独占一行没有全部利用上,但是下一个元素也是另起一行。





在资料里是查找不到这样的元素的。

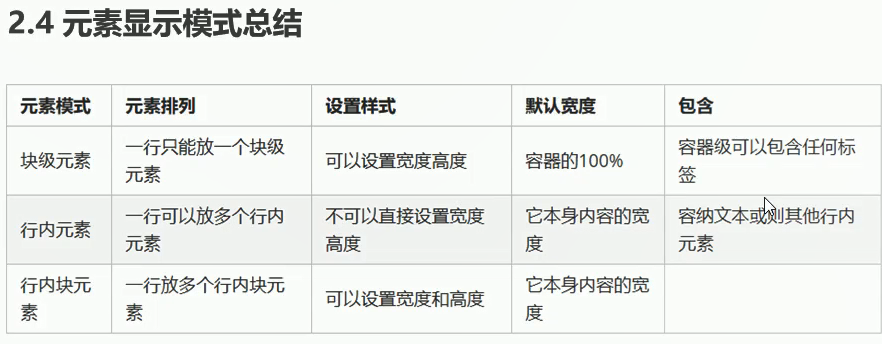

 (重点)
(重点)

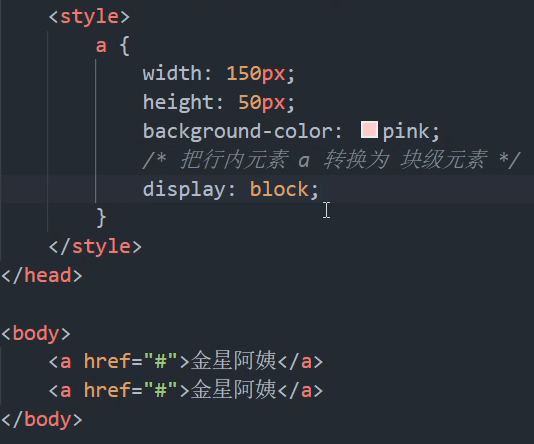


变成行内元素了宽度高度就会无效,所以代码会有波浪线。
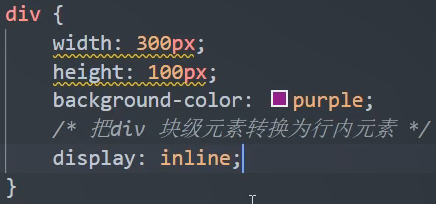
 (重点)
(重点)


一行可以放多个。



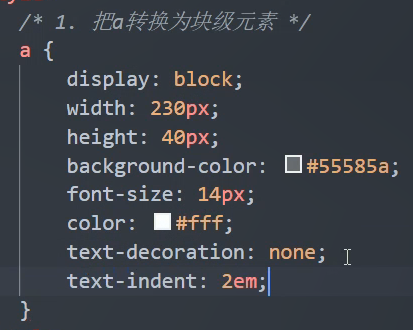

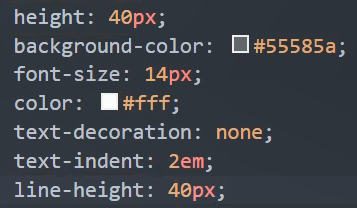
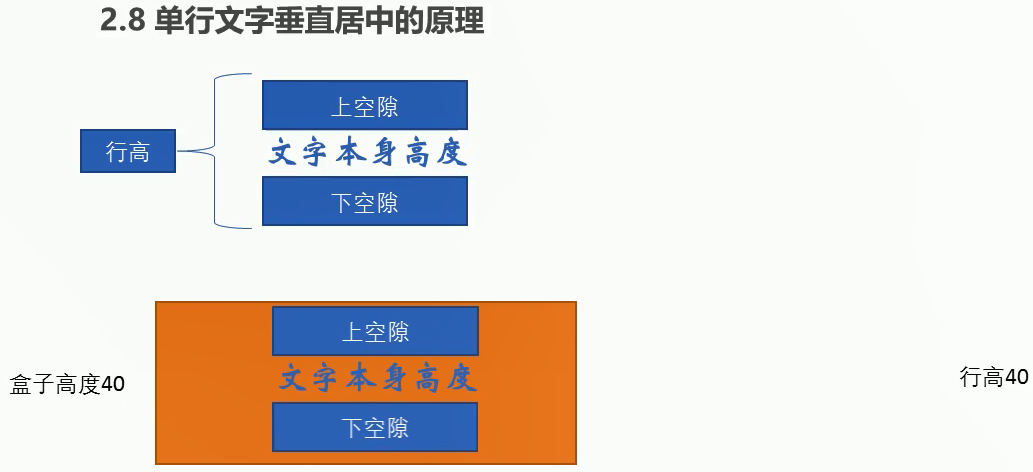
让line-height=height=40px




不写的话就是默认值transparent了!


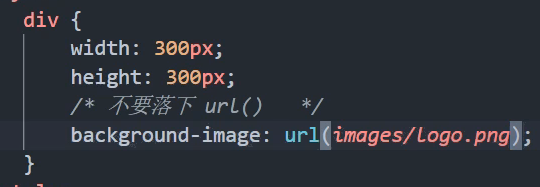



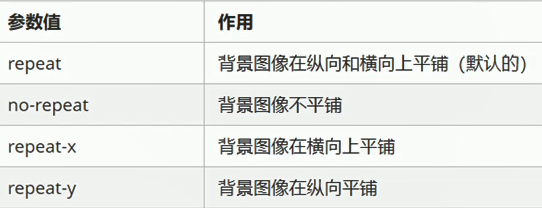




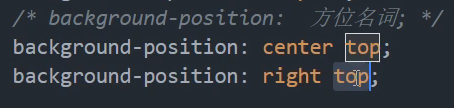




案例:

使用插入背景图片的原因:可以是一张很大的图片的核心部分显示在页面当中!边边角角的没有显示出来没关系,屏幕的放大缩小在一点点的展示边边角角部分!

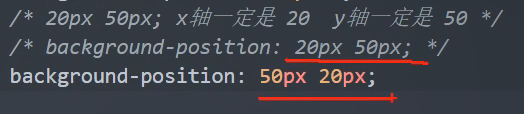
精确位置 有一个严格顺序。




scroll是默认跟着滚动的。




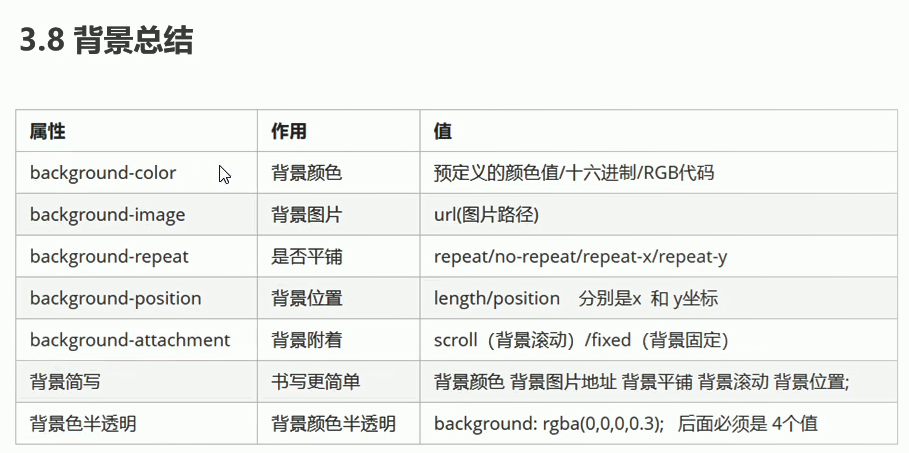



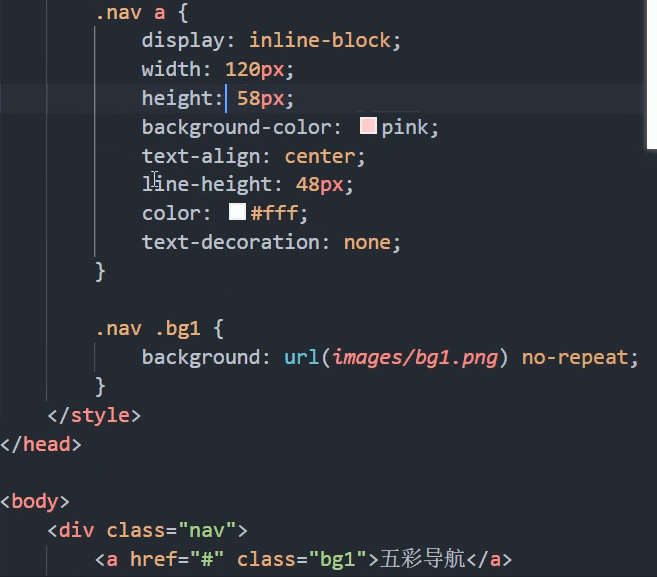
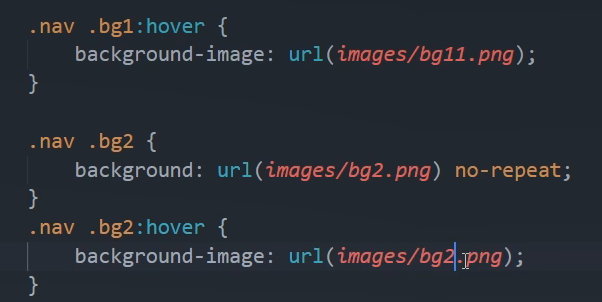
css基础02的更多相关文章
- CSS基础(02)
CSS 选择器 1.CSS3 选择器简介 在 CSS 中,选择器是一种模式,用于选择需要添加样式的元素. 语法: 下面中"CSS" 列指示该属性是在哪个 CSS 版本中定义的.(C ...
- css基础--常用css属性02
上篇地址:css基础--常用css属性01 本文参考菜鸟教程和w3school 1 浮动和清除浮动 在上篇的第十一节--定位中说道: CSS 有三种基本的定位机制:普通流.浮动和绝对定位. 普通流和 ...
- 2020年12月-第02阶段-前端基础-CSS基础选择器
CSS选择器(重点) 理解 能说出选择器的作用 id选择器和类选择器的区别 1. CSS选择器作用(重点) 如上图所以,要把里面的小黄人分为2组,最快的方法怎办? 很多, 比如 一只眼睛的一组,剩下的 ...
- CSS 基础知识点 样式 选择器 伪类
CSS 基础知识点汇集 版权声明:这篇博客是别人写的,大神博客地址 : https://www.cnblogs.com/Mtime/p/5184685.html 1.CSS 简介 CSS 指层叠样式表 ...
- 第五模块:WEB开发基础 第1章·HTML&CSS基础
01-前端介绍 02-HTML介绍 03-HTML文档结构 04-head标签相关内容 05-常用标签一之h1~h6,p,a 06-常用标签一之ul.ol.div.img.span 07-常用标签二- ...
- css 基础教程学习
css基础语法 css语法 CSS 规则由两个主要的部分构成:选择器,以及一条或多条声明. 选择器通常是您需要改变样式的 HTML 元素. 每条声明由一个属性和一个值组成. 如果要定义不止一个声明,则 ...
- CSS基础知识筑基
01.CSS 简介 CSS 指层叠样式表 (Cascading Style Sheets),对HTML网页内容进行统一外观样式设计和管理,给网页进行各种装饰,让她变得美观,是HTML的化妆师.(Cas ...
- 前端开发:css基础知识之盒模型以及浮动布局。
前端开发:css基础知识之盒模型以及浮动布局 前言 楼主的蛮多朋友最近都在学习html5,他们都会问到同一个问题 浮动是什么东西? 为什么这个浮动没有效果? 这个问题楼主已经回答了n遍.今天则是把 ...
- CSS基础总结
CSS基础总结链接地址:http://segmentfault.com/a/1190000002773955
随机推荐
- ifconfig出现bash: ifconfig:command not found解决办法之解决连环问题
Centos7中没有安装ifconfig命令的解决方法 在这之前,centos7最小化安装默认是不能联网的,首先必须切换到root用户,再解决网络问题 一. 切换到root用户 二. ...
- Redis设计与实现3.1:主从复制
主从复制 这是<Redis设计与实现>系列的文章,系列导航:Redis设计与实现笔记 SLAVEOF 新旧复制功能 旧版复制功能 旧版复制功能的实现为 同步 和 命令传播: 当刚连上Mas ...
- MAC系统下破解WIFI密码(亲测可用,含wifi密码字典)
出差第二天,住的小区因为疫情被封,宿舍又没有wifi,看着附近满满的WIFI信号列表,wifi万能钥匙却一个都连接不上,心中一万匹CNM...于是电脑连上手机热点,然后各种折腾,终于破解了一个隔壁的w ...
- Linux用户权限集中管理方案
一.问题 服务器多,各个服务器上的管理人员多,ROOT权限泛滥,经常导致文件莫名其妙丢失,老手和新手对服务器的熟知程度不同,安全存在不稳定和操作安全隐患. 二.方案 利用sudo配置指定用户只能执行指 ...
- 【Java】在IDEA中将Javafx项目打包成为可运行的.jar文件
在使用Javafx制作一个图形化界面程序的时候,我遇到了打包文件的难题. 按照网上给出的解决方案构建出来的jar文件总是没有办法运行. 以下是我最终的解决方案. 我使用的IDE是IntelliJ ID ...
- 素性测试+PollardRho
素数判定 暴力 本质上是检查其是否能够不用其本身进行质因数分解. 直接枚举从区间 \([2,n)\) 的数看其是否整除 \(n\) 即可.但是其实发现我们只要枚举到 \(\sqrt n\) 即可,复杂 ...
- [刷题] IDA*
BZOJ3041 水叮当的舞步 Description & Solution 见hzw的博客 http://hzwer.com/1507.html Code // Author: wlzhou ...
- Spring Authorization Server(AS)从 Mysql 中读取客户端、用户
Spring AS 持久化 jdk version: 17 spring boot version: 2.7.0 spring authorization server:0.3.0 mysql ver ...
- redis-server.exe双击闪退
转自 https://blog.csdn.net/qq_40361770/article/details/80454248 解决方法: 1-win+R 打开命令行 2-cd至redis目录,例如 D: ...
- 迄今微软不同时期发布的SQL Server各版本之间的大致区别,供参考查阅
通过在互联网上收集及微软官方网站等途径获取相关资料进行整理汇总出Microsoft SQL Server各个版本(SQL Server 2008 R2.SQL Server 2012.SQL Serv ...
