关于BFS

嗨，又是躺平的一天呢

下文有很多未经版权允许而私自转载，不喜勿喷

今天我来整理亿下关于 BFS 这个“高级”的东西：

首先，我不得不提亿句 关于队列 是个啥

队列（queue）是一种特殊的线性数据结构，队列中的元素也是按照入队顺 序线性的排列。

队列的结构如下图所示，队列只允许在队列的前端（队头）进行删除操作， 后端（队尾）进行插入操作

队列的特点是先进先出（FIFO，First In First Out），即最先入队列的元素 最先出队列，就和我们平时排队一个样子

那么关于队列的实现，我也寥寥的说几句吧

首先值得知道的事是

1.它分为手工队列和STL队列；（这个我们待会讲）

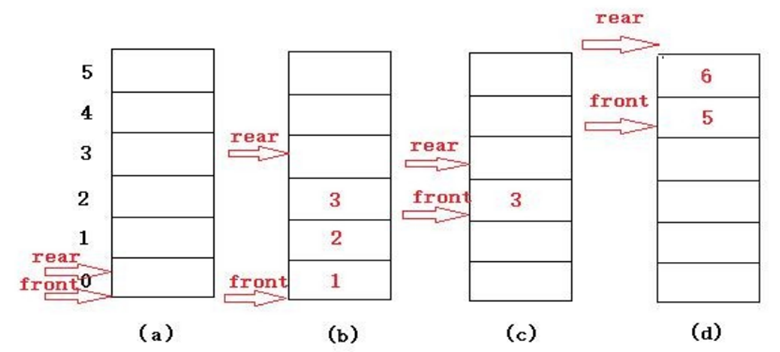
2.front代表队头，rear代表队尾（其实用head和tail也没啥区别）

3.当我们建立初始队列时，要让front和rear都等于0；

4.当在队列尾插入新元素时，让rear++，同样的，每当删除队头元素时，让front++

也就是

但是，他没你想象的那么完美：

看图，你会发现当前队列分配的最大空间为6，队列处于图(d)状态时不可能继续插入新的队尾元素---这种现象为“假溢出”

关于手工队列，它的基本思想就是这样的（我粘贴了老师的代码，不喜勿喷）

关于STL队列，只要提前调用一个queue库，就比较简洁了

那么。我们练道题试试？

代码如下

 1 #include<iostream>
 2 #include<queue>
 3 using namespace std;
 4 int main(){
 5     int n1,n2;
 6     cin>>n1>>n2;
 7     int m;
 8     cin>>m;
 9     queue<int> q1;
10     queue<int> q2;
11     for(int i=1;i<=n1;i++) q1.push(i);
12     for(int i=1;i<=n2;i++) q2.push(i);
13     for(int i=0;i<m;i++){
14         cout<<q1.front()<<' '<<q2.front()<<endl;
15         q1.push(q1.front());
16         q2.push(q2.front());
17         q1.pop();
18         q2.pop();
19     }
20     return 0;
21 }

也就是说，跳过舞的人要退出自己所在的队列，再重新到队列尾部，等待下一次被调用

OK，讲了那么多了，终于可以开始进入正题了——————

关于广度优先搜索（BFS）

其实我觉得他跟深搜有一点点的相同之处，即都是搜索（说了白说），但值得发现的不同是

DFS其实从第一个将节点开始一直往下搜，搜到最深层，接着回溯，回溯到上一个节点进行下一次搜索， 而BFS是一层一层地搜，也就是分层查找：

那么他跟队列有啥关系呢？？？

就像栈和DFS一样，比如说我有两个父节点1和2，他们的子节点分别为3,4,5和6,7  ，那么我们先将1和2放入队列中，接着进入下一行，把1删去，把他的子节点3,4,5加入队列，再把2删去，把子节点6,7加入进来，这样子就形成了一个队列，其中先进入队列的先出列，后进的自然就后出啦。

还有就是关于它的特点和性质

1.起始状态加入队列，然后每次从队列中取出一个状态，将其后继状态加入队列，后继状态指的是 由当前状态一步操作可以到达的状态，直到所有状态均被访问为止。[结点出队，并伴随扩展入队]

2、它不考虑结果的可能位置，而是彻底地搜索所有状态，所以很少有基于 BFS 的启发式算法，也很少对 BFS 进行剪枝。

3、相对于 DFS，BFS 更加难于保存当前节点的状态，所以 BFS 在爆搜中的应用较少。

4、 在某一层还没有搜索完时，是不会进入下一层的，也就是说在队列中所有同一深度的状态，是连续的一段。（这个性质在之后会用到！）

欧耶！

关于实现，呵呵，我也没办法说，因为我也不会呀呀呀

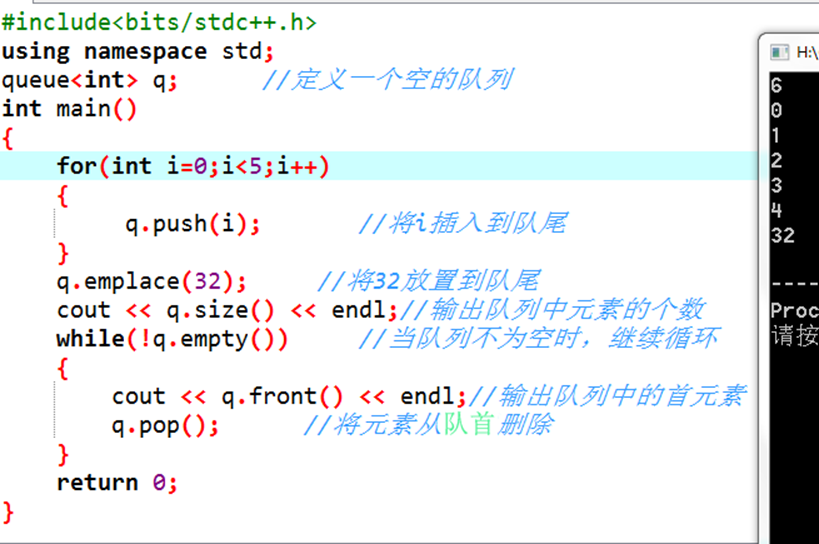
我也就只能复制粘贴了。。。

OK下面开始开摆吧

请坐稳扶好，题来啦

给出一个n*m的网格，每一个有一个颜色，两个格子之间相连当且仅当，两个格子相连且颜色相同。求联通块的数量。

输入n，m，网格输出数量

下面我来分析一下：

我们可以把每一个元素全都遍历一遍：

先从第一个元素开始，让他入队，再建一个二维数组来记录是否遍历过，如果经过，就把它标记一下，并让下一个（他上下左右的）元素进行判断，如果相同，就让他入队并给他标记，如果四周都不是了，就开始进行下一个。（即重复以上过程，对于已经被标记的元素，直接略过就好了）

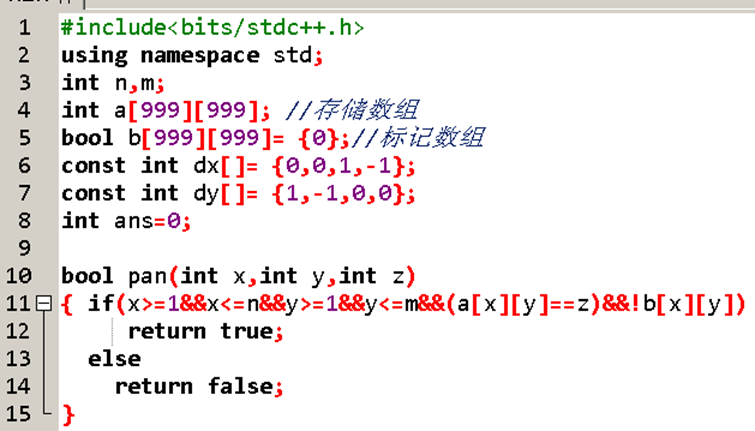
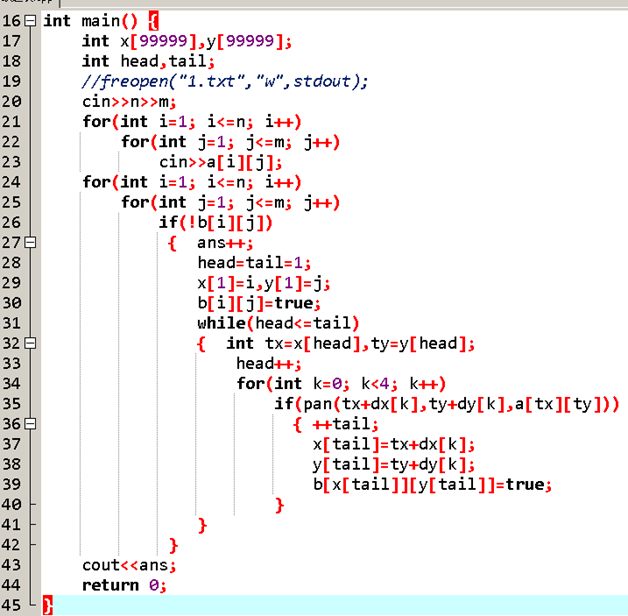
哎哎哎，先说到这吧，开摆去了

2022/3/2