An Easy Problem?! - POJ 2826(求面积)
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
using namespace std; const int MAXN = ;
const double oo = 1e4+;
const double EPS = 1e-; int sign(double val)
{
if(val > EPS)return ;
if(fabs(val) < EPS)return ;
return -;
} struct Point
{
double x, y;
Point(double x=, double y=):x(x), y(y){}
Point operator - (const Point &tmp) const{
return Point(x-tmp.x, y-tmp.y);
}
double operator ^(const Point &tmp) const{
return x*tmp.y - y*tmp.x;
}
bool operator == (const Point &tmp) const{
return fabs(x-tmp.x) < EPS && fabs(y-tmp.y) < EPS;
}
double operator *(const Point &tmp) const{
return x*tmp.x + y*tmp.y;
}
};
struct Segment
{
Point s, e;
double a, b, c;///ax + by = c
Segment(Point s=, Point e=):s(s), e(e){
a = s.y - e.y;
b = e.x - s.x;
c = e.x*s.y - s.x*e.y;
}
bool Inter(const Segment &t)const{
int v1 = sign((s-e)^(t.s-e));
int v2 = sign((s-e)^(t.e-e)); if(!v1 && !v2)return false;///共线 if(!v1 && t.s.x >= min(s.x, e.x) && t.s.x <= max(s.x, e.x)
&& t.s.y >= min(s.y, e.y) && t.s.y <= max(s.y, e.y)
|| !v2 && t.e.x >= min(s.x, e.x) && t.e.x <= max(s.x, e.x)
&& t.e.y >= min(s.y, e.y) && t.e.y <= max(s.y, e.y)
|| v1 * v2 == -)return true; return false;
}
Point CrossNode(const Segment &t) const{
Point ans;
ans.x = (c*t.b-t.c*b)/(a*t.b-t.a*b);
ans.y = (c*t.a-t.c*a)/(b*t.a-t.b*a); return ans;
}
};
double Dist(Point a, Point b)
{
return sqrt((a-b) * (a-b));
}
double Find(Point crs, Point p[], int N)
{
double sum = ; for(int i=; i<N; i++)
for(int j=i+; j<N; j++)
{
int k = sign((p[i]-crs)^(p[j]-crs)); if(p[i] == p[j])continue; if(crs.x>=min(p[i].x, p[j].x) && crs.x<=max(p[i].x, p[j].x)
|| crs.x>=p[i].x && crs.x>=p[j].x && (k>&&(p[i].x-p[j].x>EPS) || k<&&(p[j].x-p[i].x>EPS))
|| crs.x<=p[i].x && crs.x<=p[j].x && (k<&&(p[j].x-p[i].x>EPS) || k>&&(p[i].x-p[j].x>EPS)))
if(p[i].y-crs.y > EPS && p[j].y-crs.y > EPS)
{
Point A = p[i].y < p[j].y ? p[i] : p[j];
Point B = (A == p[i] ? p[j] : p[i]);
Segment t1(Point(-oo, A.y), Point(oo, A.y));
Segment t2(crs, B); B = t1.CrossNode(t2); double La = Dist(A, B);
double Lb = Dist(A, crs);
double Lc = Dist(B, crs);
double p = (La+Lb+Lc) / ; sum += sqrt(p*(p-La)*(p-Lb)*(p-Lc));
}
} return sum;
} int main()
{
int T; scanf("%d", &T); while(T--)
{
Point p[MAXN], crs; scanf("%lf%lf%lf%lf", &p[].x, &p[].y, &p[].x, &p[].y);
scanf("%lf%lf%lf%lf", &p[].x, &p[].y, &p[].x, &p[].y);
Segment L1(p[], p[]), L2(p[], p[]); double ans = ; if(L1.Inter(L2) && L2.Inter(L1))
{
crs = L1.CrossNode(L2);
ans = Find(crs, p, );
} printf("%.2f\n", ans+EPS);
} return ;
}
An Easy Problem?! - POJ 2826(求面积)的更多相关文章
- POJ 1152 An Easy Problem! (取模运算性质)
题目链接:POJ 1152 An Easy Problem! 题意:求一个N进制的数R.保证R能被(N-1)整除时最小的N. 第一反应是暴力.N的大小0到62.发现当中将N进制话成10进制时,数据会溢 ...
- hdu2601 An easy problem(数学)
题目意思: http://acm.hdu.edu.cn/showproblem.php? pid=2601 给出一个数N,求N=i*j+i+j一共同拥有多少种方案. 题目分析: 此题直接暴力模拟就可以 ...
- POJ 2826 An Easy Problem?![线段]
An Easy Problem?! Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 12970 Accepted: 199 ...
- POJ 2826 An Easy Problem? 判断线段相交
POJ 2826 An Easy Problem?! -- 思路来自kuangbin博客 下面三种情况比较特殊,特别是第三种 G++怎么交都是WA,同样的代码C++A了 #include <io ...
- POJ 2826 An Easy Problem?!
An Easy Problem?! Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 7837 Accepted: 1145 ...
- POJ 2826 An Easy Problem?! --计算几何,叉积
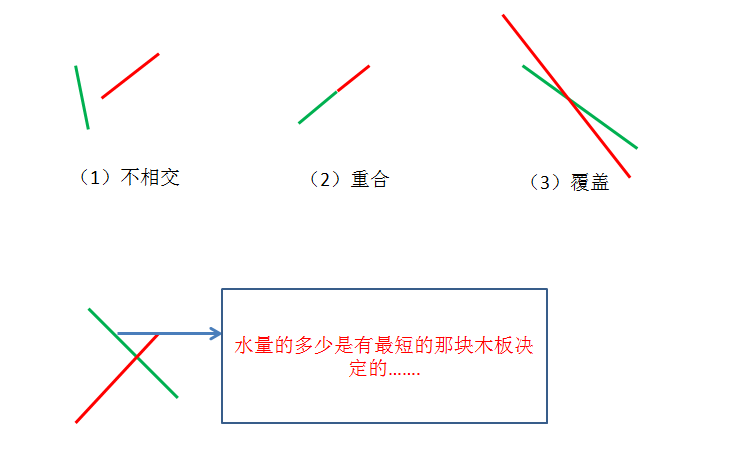
题意: 在墙上钉两块木板,问能装多少水.即两条线段所夹的中间开口向上的面积(到短板的水平线截止) 解法: 如图: 先看是否相交,不相交肯定不行,然后就要求出P与A,B / C,D中谁形成的向量是指向上 ...
- POJ 2826 An Easy Problem?! 好的标题
受该两块木板以形成槽的效果.Q槽可容纳雨水多,注意雨爆跌,思想是非常easy,分类讨论是有点差. 1.假定两条线段不相交或平行,然后再装0: 2.有一个平行x轴.连衣裙0. 3.若上面覆盖以下的,装0 ...
- 【解题报告】PKU 2826 An Easy Problem?!
原题链接:http://poj.org/problem?id=2826 一题很蛋疼的一题.目前为止还有一个问题我没搞清楚,问题注在代码中. 题目大意: 外面下雨了,农民Johnoson的bull(?? ...
- poj 3348--Cows(凸包求面积)
链接:http://poj.org/problem?id=3348 Cows Time Limit: 2000MS Memory Limit: 65536K Total Submissions: ...
随机推荐
- 时区之痒 - 从手机GPS模块获取的时间,真的是北京时间么?
去年互联网地图行业开始引入众包模式,国内比较大的地图商,比如四维图新.高德地图.百度地图纷纷开始推出UGC应用,众包给用户采集门址.公交站等信息,并按照工作量给与采集者一定的回报.我曾经玩过某德推出的 ...
- 18款js和jquery文字特效代码分享
18款js和jquery文字特效代码分享 jQCloud标签云插件_热门城市文字标签云代码 js 3d标签云特效关键词文字球状标签云代码 原生JS鼠标悬停文字球状放大显示效果代码 原生js文字动画圆形 ...
- 创建对象的两种方法: new 和 面向对象(对象字面量)及对象属性访问方法
创建对象的两种方法: new 和 面向对象(对象字面量)用 new 时:var o = new Object();o.name = "lin3615";alert(o.name); ...
- [CSS]border边框
border: 1px solid #ccc; /*1像素 实线 灰色*/可分割成:border-width:1px;border-style: solid; border-color: #00 ...
- php之面向对象(2)
注意:看这篇文章之前建议看看之前的文章,因为内容之间衔接性比较强.勿喷.. 面向对象,是一种思维模式的名字,并不是指某种特定的写法,面向对象简称oop,思路的核心在于:什么时候 什么东西 做什么. 编 ...
- TCP/IP笔记 应用层(2)——FTP
1. FTP(File Transfer Protocol) 文件传送协议 FTP 只提供文件传送的一些基本的服务,它使用 TCP 可靠的运输服务.FTP 的主要功能是减少或消除在不同操作系统下处理文 ...
- AppDomain与进程、线程、Assembly之间关系
AppDomain是CLR的运行单元,它可以加载Assembly.创建对象以及执行程序 AppDomain是CLR实现代码隔离的基本机制. 每一个AppDomain可以单独运行.停止:每个AppD ...
- shell 常用
/etc/password 用户的 home路径设置 chwon groupname:username path_or_file -R # 修改文件左右者 chomd
- 2016022602 - redis安装和启动
redis安装 我使用的是ubuntu15.1,打开终端,输入命令:sudo apt-get install redis-server 将会在本机安装上redis. 启动redis 启动redis命令 ...
- source insight 使用技巧
一.在所有文件中查找字符串 1.菜单栏选择“search project” 2.在随便一个工程文件中把所要查找的字符串输入到空白的地方,然后点连接
