ARC089E GraphXY 构造

传送门

---

在Luogu上评了”NOI“之后评级变成了”普及+/提高“……我觉得我可能要退群了

考虑构造一个这样的图：

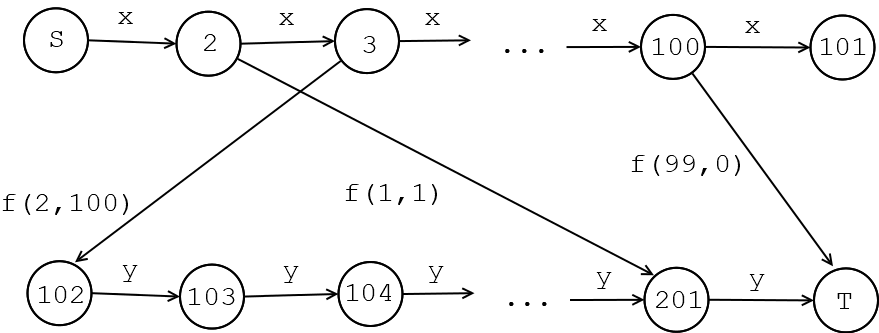
其中上半部分是从\(S\)开始的一条长\(100\)、每条边权都为\(x\)的链（长度超过\(100\)显然是没有意义的），下半部分是以\(T\)结束的一条长\(100\)、每条边权都为\(y\)的链。在这两条链中间，有\(101 \times 101\)条边（上图中只画出了部分），边权为一个矩阵\(f_{i,j}\)。如果要经过\(f_{i,j}\)对应的边，那么需要从\(S\)开始沿着上半部分的链走\(i\)步，然后经过\(f_{i,j}\)，最后沿着下半部分的链走\(j\)步到达\(T\)，总边权就是\(xi+yj+f_{i,j}\)。

在这个图中，有\(d_{x,y} = \min\limits_{a,b \geq 0} xa + yb + f_{a,b}\)，松弛条件得\(\forall a , b \geq 0 , d_{x,y} \leq xa + yb + f_{a,b}\)，即\(f_{a,b} \geq d_{x,y} - xa - yb\)。

这样可以对于每个\(f_{a,b}\)得到\(A \times B\)个不等式，可得\(f_{a,b}\)的解集。而\(f_{a,b}\)一定需要取到其中的最小值（如果不取到最小值，可能存在\(x,y\)满足\(\min\limits_{a,b \geq 0} xa + yb + f_{a,b} > d_{x,y}\)），所以可以得到\(f_{a,b}\)的确切值。然后再代入\(d_{x,y}\)的式子检验以下图是否合法即可。

时间复杂度\(O(N^3)\)

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<ctime>
#include<cctype>
#include<algorithm>
#include<cstring>
#include<iomanip>
#include<queue>
#include<map>
#include<set>
#include<bitset>
#include<vector>
#include<stack>
#include<cmath>
#include<random>
//This code is written by Itst
using namespace std;

inline int read(){
    int a = 0;
    char c = getchar();
    bool f = 0;
    while(!isdigit(c) && c != EOF)
        c = getchar();
    if(c == EOF)
        exit(0);
    while(isdigit(c)){
    a = a * 10 + c - 48;
        c = getchar();
    }
    return f ? -a : a;
}

int d[12][12] , f[107][107];

signed main(){
    int A = read() , B = read();
    for(int i = 1 ; i <= A ; ++i)
    for(int j = 1 ; j <= B ; ++j)
        d[i][j] = read();
    for(int i = 0 ; i <= 100 ; ++i)
    for(int j = 0 ; j <= 100 ; ++j)
        for(int p = 1 ; p <= A ; ++p)
        for(int q = 1 ; q <= B ; ++q)
            f[i][j] = max(f[i][j] , d[p][q] - i * p - j * q);
    for(int i = 1 ; i <= A ; ++i)
    for(int j = 1 ; j <= B ; ++j){
        int minN = 1e9;
        for(int p = 0 ; p <= 100 ; ++p)
        for(int q = 0 ; q <= 100 ; ++q)
            minN = min(minN , f[p][q] + p * i + q * j);
        if(minN != d[i][j]){
        puts("Impossible");
        return 0;
        }
    }
    puts("Possible");
    puts("202 10401");
    for(int i = 1 ; i <= 100 ; ++i)
    printf("%d %d X\n" , i , i + 1);
    for(int i = 102 ; i < 202 ; ++i)
    printf("%d %d Y\n" , i , i + 1);
    for(int i = 0 ; i <= 100 ; ++i)
    for(int j = 0 ; j <= 100 ; ++j)
        printf("%d %d %d\n" , 1 + i , 202 - j , f[i][j]);
    puts("1 202");
    return 0;
}