[数学-构造矩阵]NEFU 1113

依据题意。我已经推导出tn的公式。ti=ti.a+ti.b，ti.a=5*t(i-1).a+4*t(i-1).b，ti.b=t(i-1).a+t(i-1).b

然而以下居然不能继续推到sn的公式！！！

！

这道题考察的就是求随意数列的前n项和，在sn的递推公式不太明显的时候。用矩阵解决。

设矩阵A=。矩阵F0=

" />

那么设矩阵S=(A+A²+A³…. + Aⁿ)*F0

终于答案就是矩阵S内两个元素之和。

那么怎么求A+A²+A³…. + Aⁿ ？

能够继续构造例如以下的分块矩阵，当中 I 是单位矩阵

设R=。则有： R²=，R³=

能够发现右上角即为 I + A + A^2 + ... + A^n，多一个 I 后面给减掉就能够了

能够用高速幂求出R^n;

然而上面的方法对于此题仍然tle，看了标码发现。能通过推导进一步缩小矩阵的阶数，我这里的R是四阶。而标码里的运算仅仅有三阶。

继续思考：

看看能不能直接推导得到S的通项公式。看解说：

T[i] = dp[i][0]+dp[i][1]

=6*dp[i-1][1]+5*dp[i-1][0]

=6*T[i-1]-dp[i-1][0]

=6*T[i-1]-T[i-2]

依据S[i]=S[i-1]+T[i]能够计算出：

S[i]=S[i-1]+ 6*T[i-1]-T[i-2]

则有公式：

  

设R= 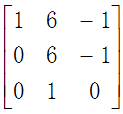，搞定！

总结：矩阵的应用，细致学习上面的构造矩阵和推导过程。第一种构造分块矩阵的方法非常实用，它对sn公式不好直接构造矩阵的时候适用。

但假设像上面S[i]=S[i-1]+ 6*T[i-1]-T[i-2]这种公式能够推导出sn的递推矩阵。能够减少复杂度。

#include<stdio.h>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
const long long mod = 1000000007;
struct Ma
{
    long long m[3][3];
};
Ma operator * (Ma a,Ma b)
{
    Ma c;
    for(int i=0; i<3; i++)
        for(int j=0; j<3; j++)
        {
            c.m[i][j] = 0;
            for (int k = 0; k < 3; k++)
            {
                c.m[i][j]+=(a.m[i][k]*b.m[k][j]);
                if(c.m[i][j]>=mod||c.m[i][j]<=-mod) c.m[i][j]%=mod;
                //c.m[i][j]%=mod;
            }
        }
    return c;
}
Ma mm[65];
long long cal(long long n)
{
    int cur=0;
    Ma ans= {1,6,-1,
             0,6,-1,
             0,1,0
            };
    while(n)
    {
        if(n&1)
        {
            ans = ans*mm[cur];
        }
        cur++;
        n>>=1;
    }
    long long tmp=41*ans.m[0][0]%mod+35*ans.m[0][1]%mod+6*ans.m[0][2]%mod+mod;
    tmp%=mod;
    while(tmp<0) tmp+=mod;
    printf("%lld\n",tmp);
    return tmp;
}
//long long ans[10000005];
int main()
{
    Ma tmp= {1,6,-1,
             0,6,-1,
             0,1,0
            };
    mm[0] = tmp;
    for(int i=1; i<64; i++) mm[i]=mm[i-1]*mm[i-1];
    long long n;
    while(scanf("%lld",&n)!=EOF)
    {
        if(n==1) puts("6");
        else if(n==2) puts("41");
        else cal(n-3);
    }
    return 0;
}