LightOj 1118 - Incredible Molecules（两圆的交集面积）

题目链接：http://lightoj.com/volume_showproblem.php?problem=1118

给你两个圆的半径和圆心，求交集的面积；

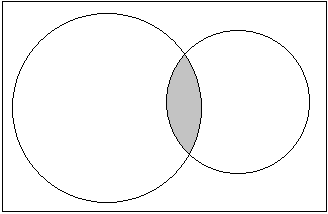
就是简单数学题，但是要注意acos得到的都是小于180度的角，所以这里要注意一下，不要求整个角，求一半的大小；这点让我错的惨不忍睹；

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <string>
#include <vector>
#include <algorithm>
#include <map>
#include <queue>
#include <stack>
#include <math.h>

using namespace std;

#define met(a, b) memset(a, b, sizeof(a))
#define N 1053
#define INF 0x3f3f3f3f
#define PI 4*atan(1)
const int MOD = ;

typedef long long LL;

int main()
{
    int T, t = ;
    scanf("%d", &T);
    while(T--)
    {
        double r1, r2, x1, x2, y1, y2;

        scanf("%lf %lf %lf %lf %lf %lf", &x1, &y1, &r1, &x2, &y2, &r2);

        double d = sqrt((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2));

        if( d >= r1+r2 )///相离或相切
        {
            printf("Case %d: %.6f\n", t++, 0.0);
            continue;
        }
        if(d <= fabs(r1-r2))///内含；
        {
            printf("Case %d: %.6f\n", t++, PI*min(r1, r2)*min(r1, r2));
            continue;
        }

        double a = acos((r1*r1+r2*r2-d*d)/(*r1*r2));
        double s = sin(a)*r1*r2;///四边形面积
        double b = acos((r1*r1+d*d-r2*r2)/(*r1*d));
        double s1 = b * r1 * r1;///r1这边的扇形面积；
        double c = acos((r2*r2+d*d-r1*r1)/(*r2*d));
        double s2 = c * r2 * r2;///r2这边的扇形面积；
        double ans = s1 + s2 - s;

        printf("Case %d: %.7f\n", t++, ans);
    }
    return ;
}
/*
Input:
5
0 0 1 10 10 1
0 0 10 0 0 5
-862 823 894 -667 402 663
548 518 145 119 828 620
777 499 712 479 314 967

Output:
Case 1: 0.0
Case 2: 78.5398163397
Case 3: 1139058.0639436883
Case 4: 56622.85922574766
Case 5: 1513681.0685423985
*/