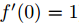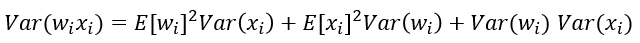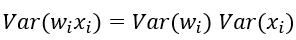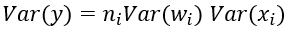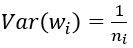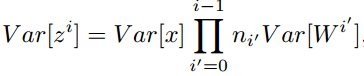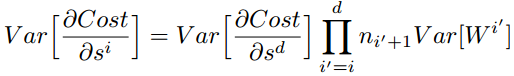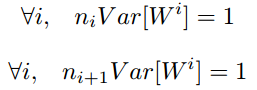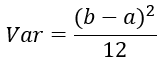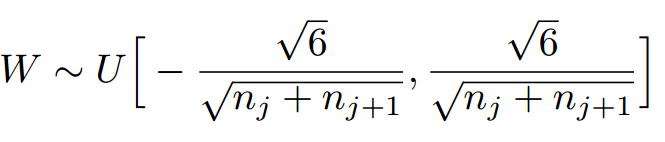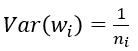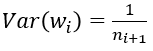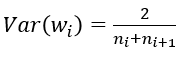神经网络权值初始化方法-Xavier

https://blog.csdn.net/u011534057/article/details/51673458

https://blog.csdn.net/qq_34784753/article/details/78668884

https://blog.csdn.net/kangroger/article/details/61414426

https://www.cnblogs.com/lindaxin/p/8027283.html

神经网络中权值初始化的方法

《Understanding the difficulty of training deep feedforward neural networks》

可惜直到近两年，这个方法才逐渐得到更多人的应用和认可。

为了使得网络中信息更好的流动，每一层输出的方差应该尽量相等。

基于这个目标，现在我们就去推导一下：每一层的权重应该满足哪种条件。

文章先假设的是线性激活函数，而且满足0点处导数为1，即 

现在我们先来分析一层卷积：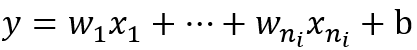 
 
其中ni表示输入个数。

根据概率统计知识我们有下面的方差公式： 

特别的，当我们假设输入和权重都是0均值时（目前有了BN之后，这一点也较容易满足），上式可以简化为： 

进一步假设输入x和权重w独立同分布，则有： 

于是，为了保证输入与输出方差一致，则应该有： 

对于一个多层的网络，某一层的方差可以用累积的形式表达： 

特别的，反向传播计算梯度时同样具有类似的形式： 

综上，为了保证前向传播和反向传播时每一层的方差一致，应满足：

但是，实际当中输入与输出的个数往往不相等，于是为了均衡考量，最终我们的权重方差应满足：

——————————————————————————————————————— 
 
———————————————————————————————————————

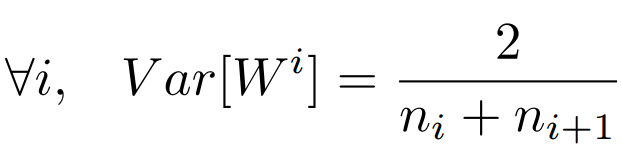
学过概率统计的都知道 [a,b] 间的均匀分布的方差为： 

因此，Xavier初始化的实现就是下面的均匀分布：

—————————————————————————————————————————— 

caffe的Xavier实现有三种选择

（1） 默认情况，方差只考虑输入个数： 

（2） FillerParameter_VarianceNorm_FAN_OUT，方差只考虑输出个数： 

（3） FillerParameter_VarianceNorm_AVERAGE，方差同时考虑输入和输出个数： 

之所以默认只考虑输入，我个人觉得是因为前向信息的传播更重要一些

———————————————————————————————————————————

Tensorflow 调用接口

https://www.tensorflow.org/api_docs/python/tf/glorot_uniform_initializer

 

tf.glorot_uniform_initializer

 

Aliases:

• tf.glorot_uniform_initializer
• tf.keras.initializers.glorot_uniform

 

tf.glorot_uniform_initializer(
    seed=None,
    dtype=tf.float32
)

Defined in tensorflow/python/ops/init_ops.py.

The Glorot uniform initializer, also called Xavier uniform initializer.

It draws samples from a uniform distribution within [-limit, limit] where limit is sqrt(6 / (fan_in + fan_out))where fan_in is the number of input units in the weight tensor and fan_out is the number of output units in the weight tensor.

Reference: http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf

Args:

• seed: A Python integer. Used to create random seeds. See tf.set_random_seed for behavior.
• dtype: The data type. Only floating point types are supported.

Returns:

An initializer.

Mxnet 调用接口

https://mxnet.apache.org/api/python/optimization/optimization.html#mxnet.initializer.Xavier

class mxnet.initializer.Xavier(rnd_type='uniform', factor_type='avg', magnitude=3)[source]

Returns an initializer performing “Xavier” initialization for weights.

This initializer is designed to keep the scale of gradients roughly the same in all layers.

By default, rnd_type is 'uniform' and factor_type is 'avg', the initializer fills the weights with random numbers in the range of [−c,c][−c,c], where c=3.0.5∗(nin+nout)−−−−−−−−−√c=3.0.5∗(nin+nout). ninnin is the number of neurons feeding into weights, and noutnout is the number of neurons the result is fed to.

If rnd_type is 'uniform' and factor_type is 'in', the c=3.nin−−−√c=3.nin. Similarly when factor_type is 'out', the c=3.nout−−−√c=3.nout.

If rnd_type is 'gaussian' and factor_type is 'avg', the initializer fills the weights with numbers from normal distribution with a standard deviation of 3.0.5∗(nin+nout)−−−−−−−−−√3.0.5∗(nin+nout).

Parameters:	rnd_type (str, optional) – Random generator type, can be 'gaussian' or 'uniform'. factor_type (str, optional) – Can be 'avg', 'in', or 'out'. magnitude (float, optional) – Scale of random number.