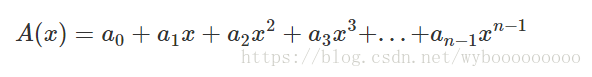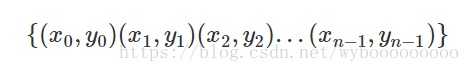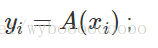FFT【快速傅里叶变换】FWT【快速沃尔什变换】
实在是 美丽的数学啊
关于傅里叶变换的博客 讲的很细致 图片非常易于理解http://blog.jobbole.com/70549/
大概能明白傅里叶变换是干吗的了
但是还是不能明白为什么用傅里叶变换来算多项式求和
在多项式中,DFT就是系数表式转换成点值表示的过程。
我们熟知的是多项式的系数表示法,通过给定一组 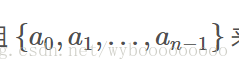
而多项式还可以有另一种表示法,称为点值表示法:
其中
可以证明,对一组互不相同的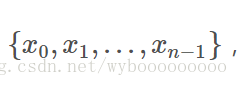
为什么要引入点值表示法这个并不“直观”的形式呢?下表显示了它的好处:
| 执行运算 | 系数表示 | 点值表示 |
|---|---|---|
| A(x)+B(x) | O(n) | O(n) |
| A(x)∗B(x) | O(n2) | O(n) |
*当然,点值表示法下的运算均要求 A(x)和 B(x) 所取的点集 {x0,x1,...,xn−1}是相同的,且运算出的 C(x) 也为点值表示法。
FFT只是快速的求DFT的方法罢了,不是一个新的概念。 在ACM-ICPC竞赛中, FFT算法常被用来为多项式乘法加速。
FFT原理就是通过奇偶分开,把规模减半,递归分治 在O(nlogn)时间内完成DFT运算
普通的计算多项式乘法的计算,时间复杂度O(n2)O(n2)。而FFT先将多项式点值表示(O(nlogn)),在O(n)下完成对点值的乘法,再以O(nlogn)O(nlogn)完成IFFT,重新得到系数表示。
利用FFT求卷积
普通的计算多项式乘法的计算,时间复杂度O(n2)O(n2)。而FFT先将多项式点值表示(O(nlogn)),在O(n)下完成对点值的乘法,再以O(nlogn)完成IFFT,重新得到系数表示。
步骤一(补0)
在两个多项式前面补0,得到两个2n次多项式,设系数向量分别为v1v1和v2v2。
步骤二(求值)
使用FFT计算f1=DFT(v1)和f2=DFT(v2)。则f1f1与f2f2为两个多项式在2n2n次单位根处的取值(即点值表示)。
步骤三(乘法)
把f1f1与f2f2每一维对应相乘,得到ff,代表对应输入多项式乘积的点值表示。
步骤四(插值)
使用IFFT计算v=IDFT(f),其中vv就是乘积的系数向量。
综上
fft(x1, len, 1);
fft(x2, len, 1);
for (int i = 0;i < len;i++) {
x[i] = x1[i] * x2[i];
}
fft(x, len, -1);FFT算法步骤:https://wenku.baidu.com/view/8bfb0bd476a20029bd642d85.html
kuangbin模板:
const double PI = acos(-1.0);
//复数结构体
struct complex
{
double r,i;
complex(double _r = 0.0,double _i = 0.0)
{
r = _r; i = _i;
}
complex operator +(const complex &b)
{
return complex(r+b.r,i+b.i);
}
complex operator -(const complex &b)
{
return complex(r-b.r,i-b.i);
}
complex operator *(const complex &b)
{
return complex(r*b.r-i*b.i,r*b.i+i*b.r);
}
};
/*
* 进行FFT和IFFT前的反转变换。
* 位置i和 (i二进制反转后位置)互换
* len必须去2的幂
*/
void change(complex y[],int len)
{
int i,j,k;
for(i = 1, j = len/2;i < len-1; i++)
{
if(i < j)swap(y[i],y[j]);
//交换互为小标反转的元素,i<j保证交换一次
//i做正常的+1,j左反转类型的+1,始终保持i和j是反转的
k = len/2;
while( j >= k)
{
j -= k;
k /= 2;
}
if(j < k) j += k;
}
}
/*
* 做FFT
* len必须为2^k形式,
* on==1时是DFT,on==-1时是IDFT
*/
void fft(complex y[],int len,int on)
{
change(y,len);
for(int h = 2; h <= len; h <<= 1)
{
complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
for(int j = 0;j < len;j+=h)
{
complex w(1,0);
for(int k = j;k < j+h/2;k++)
{
complex u = y[k];
complex t = w*y[k+h/2];
y[k] = u+t;
y[k+h/2] = u-t;
w = w*wn;
}
}
}
if(on == -1)
for(int i = 0;i < len;i++)
y[i].r /= len;
}沃尔什变换https://www.cnblogs.com/ACMLCZH/p/8022502.html
主要功能是求: ,其中
,其中 为集合运算符。
为集合运算符。
就像FFT一样,FWT是对数组的一种变换,我们称数组X的变换为FWT(X)。
所以FWT的核心思想是:
为了求得C=A★B,我们瞎搞搞出一个变换FWT(X),
使得FWT(C)=FWT(A)  FWT(B),然后根据FWT(C)求得C。
FWT(B),然后根据FWT(C)求得C。
(其中★表示卷积运算, 表示将数组对应下标的数相乘的运算)
表示将数组对应下标的数相乘的运算)
也就是说我们可以通过FWT(X)变换把复杂度O(n^2)的★运算变为O(n)的 运算。
运算。
跟FFT是完全相同的。所以我们考虑怎么搞出这个FWT(X)。
FFT【快速傅里叶变换】FWT【快速沃尔什变换】的更多相关文章
- 快速傅里叶变换与快速数论变换瞎学笔记$QwQ$
$umm$先预警下想入门$FFT$就不要康我滴学习笔记了,,, 就,我学习笔记基本上是我大概$get$之后通过写$blog$加强理解加深记忆这样儿的,有些姿势点我可能会直接$skip$什么的,所以对除 ...
- FFT —— 快速傅里叶变换
问题: 已知A[], B[], 求C[],使: 定义C是A,B的卷积,例如多项式乘法等. 朴素做法是按照定义枚举i和j,但这样时间复杂度是O(n2). 能不能使时间复杂度降下来呢? 点值表示法: 我们 ...
- 快速傅里叶变换FFT / NTT
目录 FFT 系数表示法 点值表示法 复数 DFT(离散傅里叶变换) 单位根的性质 FFT(快速傅里叶变换) IFFT(快速傅里叶逆变换) NTT 阶 原根 扩展知识 FFT 参考blog: 十分简明 ...
- Fast Fourier Transform ——快速傅里叶变换
问题: 已知$A=a_{0..n-1}$, $B=b_{0..n-1}$, 求$C=c_{0..2n-2}$,使: $$c_i = \sum_{j=0}^ia_jb_{i-j}$$ 定义$C$是$A$ ...
- 快速傅里叶变换(FFT)详解
本文只讨论FFT在信息学奥赛中的应用 文中内容均为个人理解,如有错误请指出,不胜感激 前言 先解释几个比较容易混淆的缩写吧 DFT:离散傅里叶变换—>$O(n^2)$计算多项式乘法 FFT:快速 ...
- 快速傅里叶变换(FFT)_转载
FFTFFT·Fast Fourier TransformationFast Fourier Transformation快速傅立叶变换 P3803 [模板]多项式乘法(FFT) 参考上文 首 ...
- 浅谈FFT(快速傅里叶变换)
前言 啊摸鱼真爽哈哈哈哈哈哈 这个假期努力多更几篇( 理解本算法需对一些< 常 用 >数学概念比较清楚,如复数.虚数.三角函数等(不会的自己查去(其实就是懒得写了(¬︿̫̿¬☆) 整理了一 ...
- [学习笔记] 多项式与快速傅里叶变换(FFT)基础
引入 可能有不少OIer都知道FFT这个神奇的算法, 通过一系列玄学的变化就可以在 $O(nlog(n))$ 的总时间复杂度内计算出两个向量的卷积, 而代码量却非常小. 博主一年半前曾经因COGS的一 ...
- FWT快速沃尔什变换学习笔记
FWT快速沃尔什变换学习笔记 1.FWT用来干啥啊 回忆一下多项式的卷积\(C_k=\sum_{i+j=k}A_i*B_j\) 我们可以用\(FFT\)来做. 甚至在一些特殊情况下,我们\(C_k=\ ...
随机推荐
- web实现QQ头像上传截取功能
由于最近一段时间比较忙,发现好久没写博客了,给大家分享下最近搞的logo上传截取功能.在实现这个功能之前找了一些jq的插件,最后选定了cropper在github中可以找到. 具体的思路是1:选择上传 ...
- DBA操作
sqlplus sys/tiger as sysdba; alter user scott account unlock; 用户已更改 切换用户:conn scott/tiger as sysdba ...
- 8 -- 深入使用Spring -- 3...4 在ApplicationContext中使用资源
8.3.4 在ApplicationContext中使用资源 不管以怎样的方式创建ApplicationContext实例,都需要为ApplicationContext指定配置文件,Spring允许使 ...
- 屏蔽win10中文输入法
Windows 10自带的默认输入法,是通过Shift键来切换中/英文,这样为玩一些不需要打字,却需要使用Shift键的游戏带来了不便,比如,在进行游戏的时候,按下Shift键后,再按跳跃.射击等键, ...
- linux 信息收集脚本。转自insight-labs
找出所有.sh .pl .py .conf .cnf .ini .*history .*pass* (/usr/share目录里面的除外) 并且在当前目录zip打包.有些时候很多配置文件的权限配置不严 ...
- 关于Kafka幂等producer的讨论
众所周知,Kafka 0.11.0.0版本正式支持精确一次处理语义(exactly once semantics,下称EOS).Kafka的EOS主要体现在3个方面: 幂等producer:保证发送单 ...
- 用Copy命令合并文件
用Copy命令合并文件 这个文章是在我以前的百度空间里面发表过的,后来因为某个内分泌失调的管理员把我的空间http://hi.baidu.com/kamdy 封了! 旧事不提,还是回到主题吧,这个 ...
- pg3 bypass源码阅读 —— 学习x64内核hook跳板技术
如之前描述的 pg3复杂了许多 先来看看都要hook哪些点 1.hook dpc和定时器分发器,防止seh路线触发pg KiTimerListExpire,KiRetireDpcList 看一下hoo ...
- 使用filezilla连接树莓派失败
报错: 错误: Network error: Connection refused 错误: 无法连接到服务器 原因是新版的树莓派系统默认关闭ssh,进入树莓派打开ssh即可. sudo service ...
- 深入理解 Neutron -- OpenStack 网络实现(3):VXLAN 模式
问题导读1.VXLAN 模式下,网络的架构跟 GRE 模式类似,他们的不同点在什么地方?2.网络节点的作用是什么?3.tap-xxx.qr-xxx是指什么? 接上篇:深入理解 Neutron -- O ...