【Beta版本发布】爬虫队长装备全面更新！

一、Beta阶段目标回顾

---

　　1.为了解决Alpha阶段线程异常泛滥的问题，我们需要一个线程池。

　　2.为了爬取得到的文件正确可用，我们需要一个异常清理器。

　　3.为了不间断爬取，管理员不必频繁运行程序点，我们需要实现动态爬取。

　　以上的三个主要目标在Beta开发阶段都得到了实现，除此以外，因为我们本次开发模式是“集市”，根据其他相关小组的需求我们还额外实现了两个主要功能：

　　1.视频链接的大量爬取。

　　2.基于祖先网页的专门爬取。

二、更新内容

---

 1 新增功能

1.1 动态爬取

　　在Alpha阶段中，如果在爬虫正在运行的过程中，我们想要加入新的种子链接，就不得不关闭当前的爬取动作，重新运行程序后添加进行爬取。

　　这样的操作造成如下多个不良影响：

　　1.爬取的内容重复冗余性增加。

　　2.因为每个种子网页的最大爬取数目是不可预见的，管理员需要经常留意当前爬取动作是否已停止，进而决定是否重新运行程序爬取新网页。

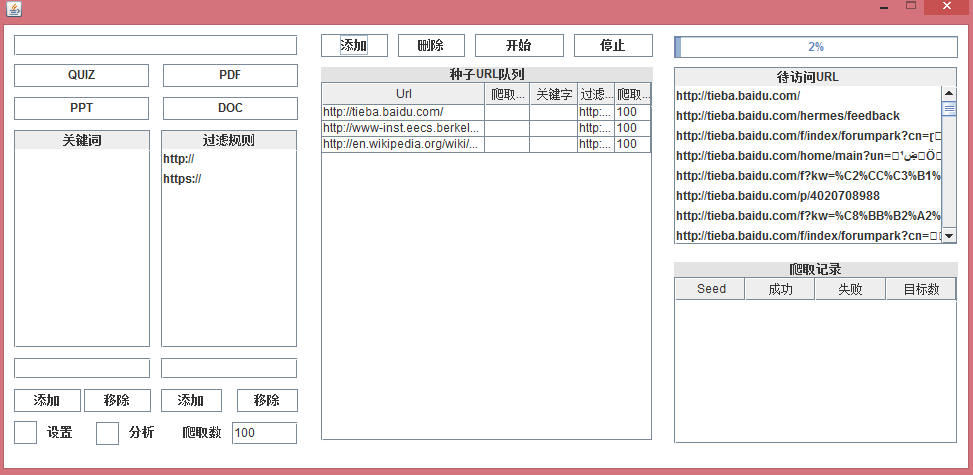
　　动态爬取是能够在爬虫运行时不停止爬虫当前的爬取动作而添加种子URL，管理员可以在任何需要的时候进行添加动作。新功能在解决了以上两个不良影响的同时，还具备以下几个优势：

　　1.能为每个种子URL设定爬取数目。

　　2.时间容错性大，能够允许任何时间进行操作。

　　3.不必繁琐的关闭和重新运行程序，操作简易。

　　如下是两种动态爬取功能，第一种为根据当前爬取数目是否达到要求来决定已添加的种子URL是否入列，第二种为根据时间周期来入列。　　

　　

1.2 视频链接爬取

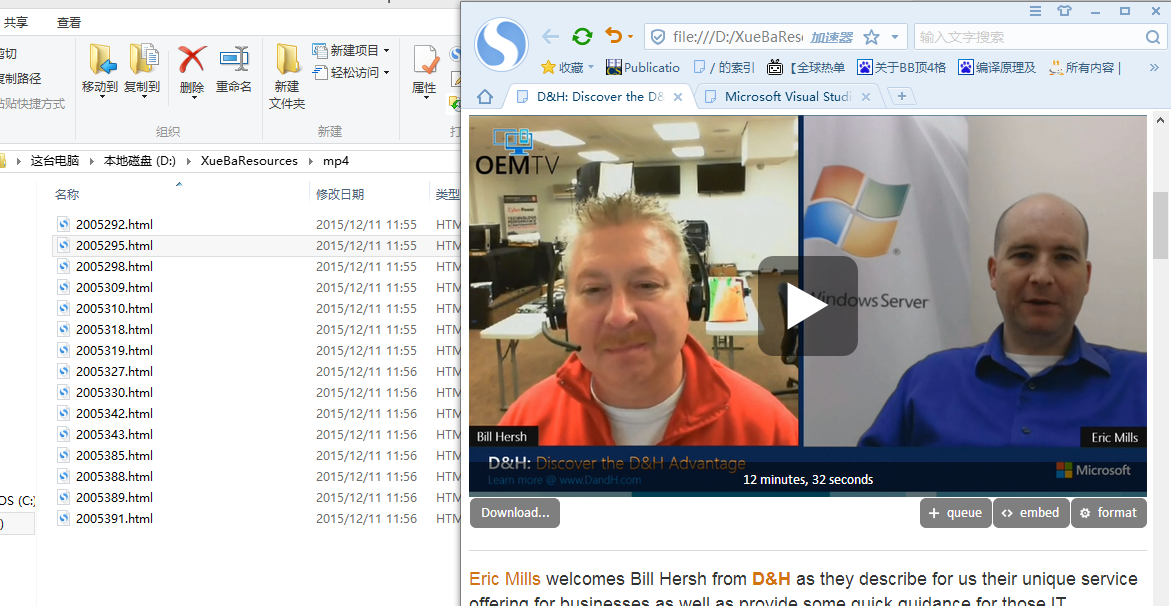
　　设计了多个对视频链接的判定条件，由子链存在视频文件回溯到父链接，实现视频链接的爬取。选择爬取视频链接而非视频文件有如下考虑：

　　1.视频文件较大，下载速度慢，而视频链接既能满足对视频的需求，并且大小和普通网页并无二致。

　　2.其他小组的需求。

　　

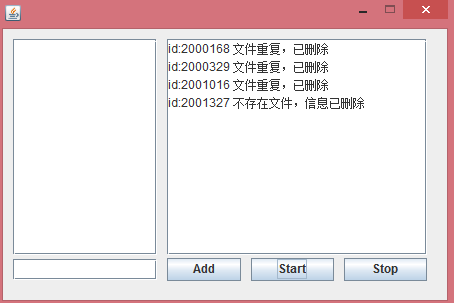
1.3 异常清理器

　　通过对Alpha阶段已爬取的文件和数据库的检查我们发现如下多个问题：

　　1.存在数据库所存文件信息在文件夹中找不到的情况。

　　2.存在数据库中存储路径为Null的情况。

　　3.存在重复文件的情况。

　　我们对以上多种异常情况进行分析，发现影响因素较多：Alpha版本爬虫无动态爬取而频繁运行程序导致的重复下载；某些网页不提供下载权限等等。我们根据分析认为难以解决以上所有影响因素，并且数据库和文件夹已然储存着异常信息。所以设计了异常清理器，专门的告知并对异常进行清理。

　　

1.4 线程池

　　针对线程异常不可控，难调试的问题，该阶段我们专门实现了线程池，通过控制程序线程的数量并对线程异常问题进行处理，使得网页的最大爬取数，最大爬取时间都有增加，已在测试报告中列出。

1.5 通过过滤规则实现子孙网页“血统纯正”。

　　在“集市”的开发过程中我们发现经常有这样一种需求：给我们一个种子URL进行爬取，但我们不希望爬到其他领域的链接中。例如我们需要爬cnblogs上的博文，但我们不需要爬取cnblogs过程可能链接出去的百度、搜狐等网页。因此我们通过过滤规则来保证子孙网页与种子网页的联系。

　　如下我们输入了一个过滤规则：http://tieba.baidu.com/。则所有不含有http://tieba.baidu.com/的网页我们都不需要。

　　

2 主要BUG修复

　　以下为修复时间较长，影响较大的BUG修复：

　　1.修复了一个过滤器BUG，该BUG会导致爬虫过滤器过滤掉大量的正常网页。

　　2.修复了一个爬取过程中的判断BUG，该BUG会导致在单次爬取动作中可能爬到具有重复URL。

　　3.修复了一个队数据库操作的BUG，将更新数据库的方法改为异步互斥更新方式，保证了同一时间只有一个线程占用数据库，保证了数据库数据的正确性，同时避免了SQLException。

3 相关优化

　　1.优化了对数据库数据的统计操作，使得Analyze响应时间更快。

　　2.优化了进行爬取时对进度显示以及对数据库操作的方法，使得单位时间爬取的网页数目更多（详情见测试报告）。

　　3.优化了爬取方式，把网页、pdf、ppt等各文档文件的爬取和下载功能充分联系到一起，提高了爬取效率。同时删减了相应的代码文件，减少了代码量。

三、环境要求

---

操作系统要求	windows XP、windows 7、windows 8
运行环境要求	最新版本的JRE
数据库要求	Sql Server 2008及以上

四、安装方法

---

　　把jar可执行文件复制到本地即可。

五、已知的缺陷与限制

---

　　a)界面的功能键会因不规范操作而导致卡死。

六、发布方式和发布地址

---

　　该版本爬虫部署在服务器10.2.26.60上，可自行拷贝试用。