MobaXterm v10.9破解
去官网下载个人版
Exeinfo查壳发现无壳
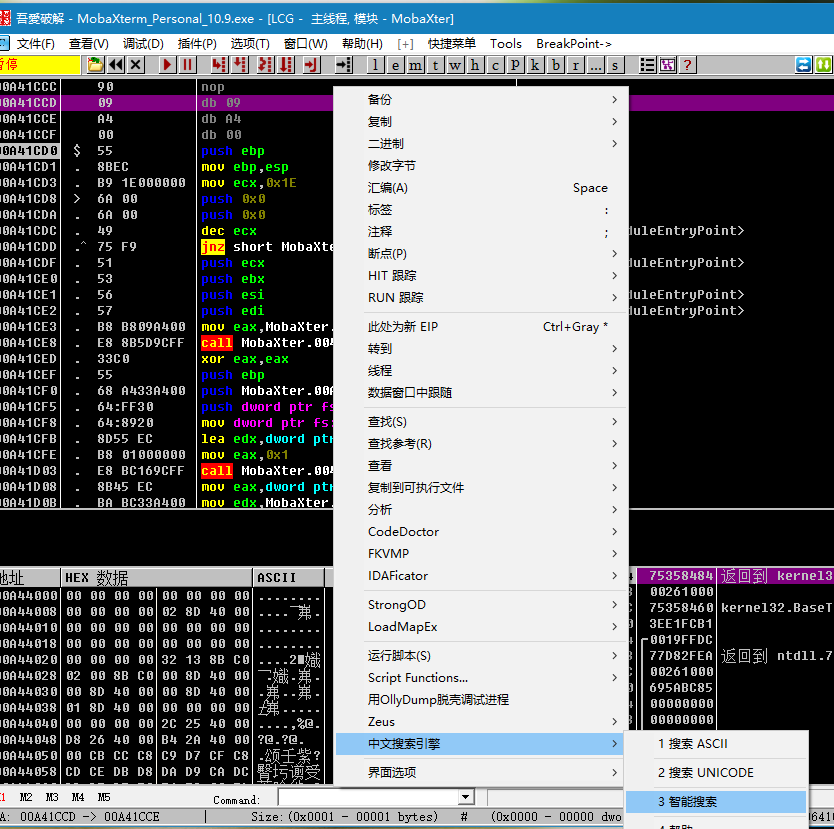
载入OD,右键,字符串智能搜索。
Ctrl+F搜索关键词About,找到到FormAbout处,即关于窗体的创建和显示的位置。双击查看汇编代码
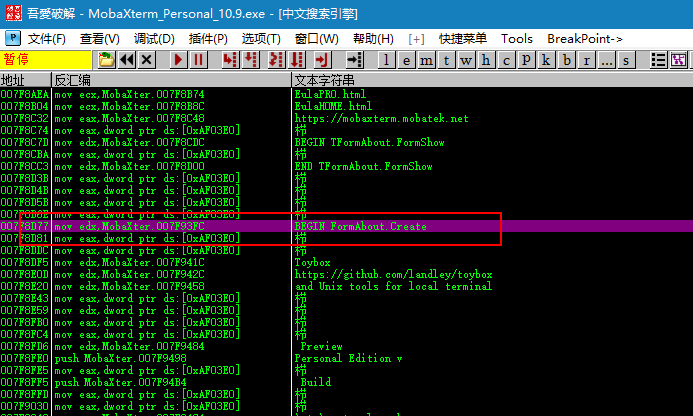
程序在窗体创建前,先读取和判断自身是否已注册为专业版。往上看,发现有个跳转,这个跳转跳过了一个清零赋值操作。这个清零赋值是最为关键的赋值,如果这个变量被赋值0,就会成为个人免费版。想要专业版的话,这个变量必须为1。我们可以直接把这个清零的操作改为赋值1。而且这个变量的清零不止一处。我们可以尝试搜索一下这行代码。一共有14处。
mov dword ptr ds:[eax+0xC9C],edx
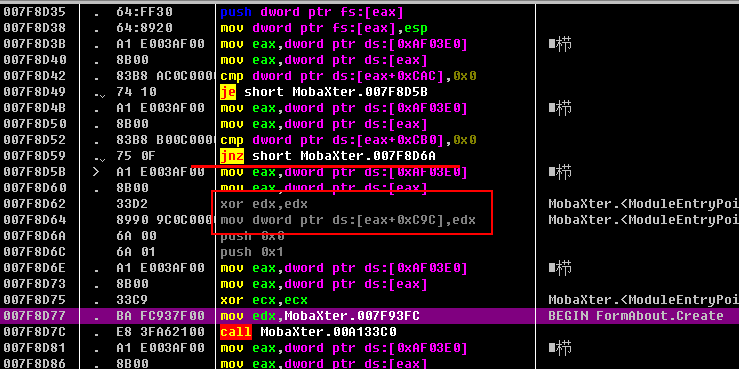
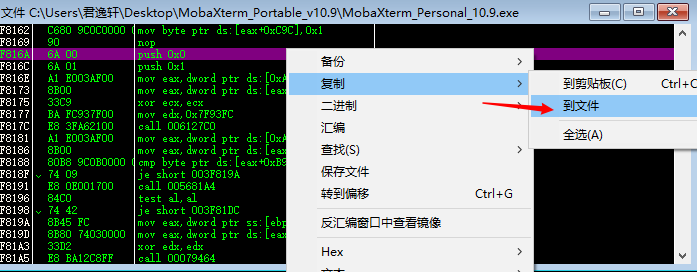
我们依次对每处代码进行修改,选中这句
xor edx,edx
把此处汇编代码修改为
mov byte ptr ds:[eax+0xC9C],
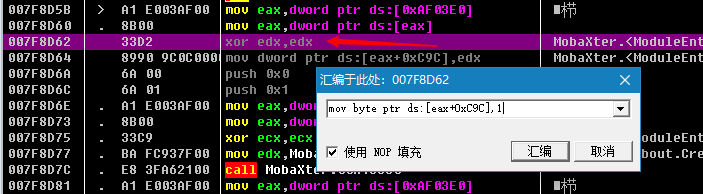
修改完毕后是这样。
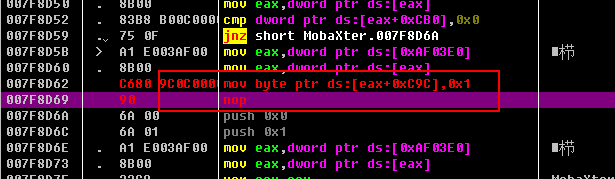
将一共14处这样的位置修改完毕后,保存修改的文件
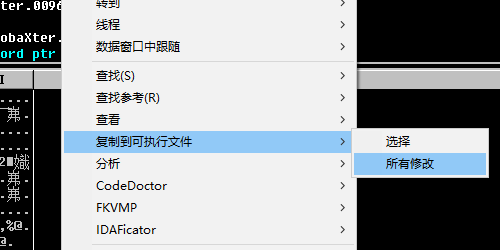
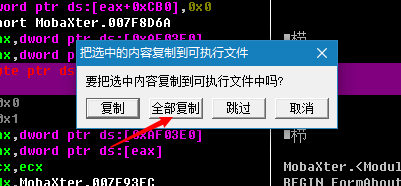
执行的时候可能会弹出一个框,提示不是正版,不过只会出现一次,不影响后面使用。
破解完毕。

附v11.0破解版:
链接: https://pan.baidu.com/s/1thfncXI-AaMfB_Dex2iNeQ
提取码: xqpv
参考文章
https://www.52pojie.cn/thread-704974-1-1.html
MobaXterm v10.9破解的更多相关文章
- Acunetix Web Vulnarability Scanner V10.5 详细中文手册
目录: 0×00.什么是Acunetix Web Vulnarability Scanner ( What is AWVS?) 0×01.AWVS安装过程.主要文件介绍.界面简介.主要操作区域简介(I ...
- awvs 中文手册详细版
目录: 0×00.什么是Acunetix Web Vulnarability Scanner ( What is AWVS?) 0×01.AWVS安装过程.主要文件介绍.界面简介.主要操作区域简介(I ...
- AWVS使用手册
目录: 0×00.什么是Acunetix Web Vulnarability Scanner ( What is AWVS?) 0×01.AWVS安装过程.主要文件介绍.界面简介.主要操作区域简介(I ...
- awvs 中文手册详细版(含10.5及12版本)
目录: 0×00.什么是Acunetix Web Vulnarability Scanner ( What is AWVS?) 0×01.AWVS安装过程.主要文件介绍.界面简介.主要操作区域简介(I ...
- 关与 Visual.Assist.X.V10.7.1912的Crack破解补丁(vs 番茄插件的key破解方法)
在win7系统下, 我用的是vs2012版本号. Visual Assist沿用了快10年的界面,最终有了更新,变得更加适合Win8 以及 VS2012的主题风格了 ,这也是以后软件的发展趋势,仅仅是 ...
- 全新思维导图 XMind ZEN v10.0.0 中文破解版
http://www.carrotchou.blog/20331.html 官网 https://www.xmind.cn/ 注意事项 破解版本已经去除了全部的官方试用版的限制,让大家可以像正版用户一 ...
- VMware Workstation(虚拟机)v10.0.1 简体中文破解版
http://www.xp510.com/xiazai/ossoft/desktools/22610.html
- MobaXterm.9.4|ssh连接工具
在狂博客中,无意发现的一款集成的远程连接工具MobaXterm.9.4,官方有个人免费版,和企业版!有连接数限制,此款为破解版.感觉还挺不错的,ssh远程连接工具! 01.主界面 02.可选的远程 ...
- centos 7 DenyHosts 安装 防暴力破解ssh登陆
为了减少软件扫描ssh登陆 还是用这个比较好点 默认端口号22 也要改 登陆密码也不要使用 弱口令 123456 这样的 Description DenyHosts is a python prog ...
随机推荐
- 图片预览组件PhotoView
图片预览组件PhotoView PhotoView是一款图片预览组件,广泛应用于大图的查看.该组件支持图片手势缩放.旋转等功能.它可以很好的和ViewPager.Picasso等组件结合,实现各种复杂 ...
- hihoCoder 1143 : 骨牌覆盖问题·一(递推,矩阵快速幂)
[题目链接]:click here~~ 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 骨牌,一种古老的玩具.今天我们要研究的是骨牌的覆盖问题: 我们有一个2xN的长条形 ...
- C++ 线段树—模板&总结
在信息学竞赛中,经常遇到这样一类问题:这类问题通常可以建模成数轴上的问题或是数列的问题,具体的操作一般是每次对数轴上的一个区间或是数列中的连续若干个数进行一种相同的处理.常规的做法一般依托于线性表这种 ...
- ubuntu下使用nvm安装nodejs
sudo apt-get install curl curl -o- https://raw.githubusercontent.com/creationix/nvm/v0.33.6/install. ...
- python系统编程(一)
进程的创建-fork 1. 进程 VS 程序 编写完毕的代码,在没有运行的时候,称之为程序 正在运行着的代码,就成为进程 进程,除了包含代码以外,还有需要运行的环境等,所以和程序是有区别的 2. fo ...
- js间隔一段时间打印数据库中的值
https://blog.csdn.net/qq_33599109/article/details/78417474
- 数据结构 BM算法
BM算法是比KMP算法更快的字符串模式匹配算法.BM算法最好情况下的时间复杂度是O(n),KMP算法最好情况下的时间复杂度是O(n+m),两者最坏情况下的时间复杂度均是O(m*n).其中,n指目标串长 ...
- Set集合架构和常用实现类的源码分析以及实例应用
说明:Set的实现类都是基于Map来实现的(HashSet是通过HashMap实现的,TreeSet是通过TreeMap实现的). (01) Set 是继承于Collection的接口.它是一个不允许 ...
- word2vec skip-gram系列2
Word2Vec的CBOW模型和Skip-gram模型 故事先从NNLM模型说起,网络结构图如下图所示,接下来先具体阐述下这个网络, 输入是个one-hot representation的向量.比如你 ...
- macOS Sierra WiFi connecting problem
吐槽一下,苹果的质量管控越来越差了. macOS Sierra有时突然或升级后会遇到wifi不停重连连不上问题,现象为不停地连接wifi. 网上有人说删除 /Library/Preferences/S ...
