线性DP之免费馅饼

题目

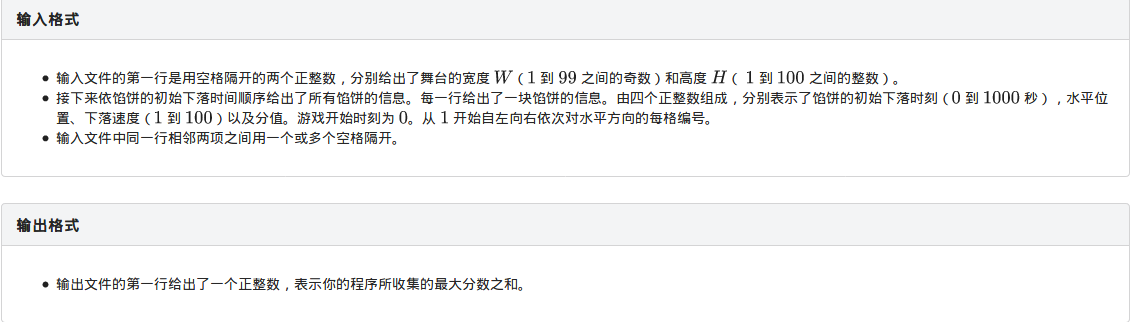
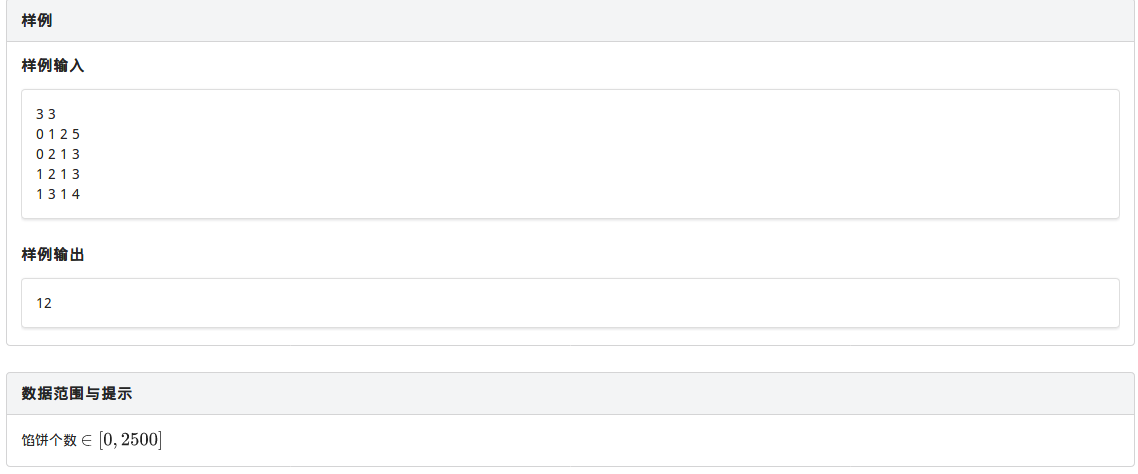
思路

线性DP，思路很容易就能想到，f[i][k]数组定义为第i秒在k位置时从上一位置j转移过来的最优解，易得f[i][k]=max(f[i][k],f[i-1][j]+search(i,k));

这里提一下本题一些细节

• 高度为1时，0时刻中间的馅饼必吃，都到嘴边了，难道要扔掉？
• 再就是在第i秒时，人可在的位置是有限的，数据比较小，容易忘掉这个点，即第i秒人的位置只能在(w+1)/2-i2和(w+1)/2+i2之间、

接下来是代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1500;
int f[maxn][150];
struct egde{
	int t,x,w;
}a[2500+10];
int w,h;
int tt,cnt,v,X,wp;
int search(int t,int x){
	int w=0;
	for(int i=1;i<=cnt;i++){
		if(a[i].t==t && a[i].x==x){
			w+=a[i].w;
		}
	}
	return w;
}
int main(){
	cin>>w>>h;
	int tmax=0;
	while(scanf("%d%d%d%d",&tt,&X,&v,&wp)!=EOF){
		a[++cnt].x=X;
		a[cnt].w=wp;
		if((h-1)%v==0){
			a[cnt].t=tt+(h-1)/v;
			tmax=max(tmax,a[cnt].t);
		}
	}
	if(h==1){
		for(int i=1;i<=cnt;i++){
			if(a[i].t==0 && a[i].x==(w+1)/2)f[0][(w+1)/2]=a[i].w;
		}
	}
	for(int i=1;i<=tmax;i++){
		for(int j=(w+1)/2-(i-1)*2;j<=(w+1)/2+(i-1)*2;j++){
			int l=j-2,r=j+2;
			if(j-2<1)l=1;
			if(j+2>w)r=w;
			for(int k=l;k<=r;k++){
				f[i][k]=max(f[i][k],f[i-1][j]+search(i,k));
			}
		}
	}

	int ans=0;
	for(int i=1;i<=w;i++){
		if(i>=(w+1)/2-tmax*2 && i<=(w+1)/2+tmax*2)
			ans=max(ans,f[tmax][i]);
	}
	cout<<ans;
}