EM算法（3）：EM算法运用

目录

EM算法（1）：K-means 算法

EM算法（2）：GMM训练算法

EM算法（3）：EM算法运用

EM算法（4）：EM算法证明

　　　　　　　　　　　　　　EM算法（3）：EM算法运用

1. 内容

　　EM算法全称为 Expectation-Maximization 算法，其具体内容为：给定数据集$\mathbf{X}=\{\mathbf{x}_1,\mathbf{x}_2,...,\mathbf{x}_n\}$，假定这个数据集是不完整的，其还缺失了一些信息Y，一个完整的样本Z = {X,Y}。而且假定如果我们能得到完整样本信息的话，训练模型就有闭式解（这个假定对于EM算法理论上可以没有，但是实际操作时我们还是要选定这样的完整信息）。那么EM算法分为两步，第一步（E-step），根据前一步得到的参数$\theta^{(i)}$，计算目标函数的期望$Q(\theta;\theta^{(i)})$:

　　　　　　　　　　　　$Q(\theta;\theta^{(i)}) = E_Y[lnp(X,Y|\theta) | X,\theta^{(i)}]$

　　　　　　　　　　　　　　　　$=\int lnp(X,Y|\theta)\cdot p(Y|X,\theta^{(i)})dY$

　　第二步，选择一个$\theta^{(i+1)}$，使得$Q(\theta;\theta^{(i)})$最大化。

2. EM算法在GMM模型上的运用

　　上面讲的EM算法大家肯定觉得很空洞、无法理解，这样就对了，光看这个肯定是看不出什么来的，这个时候就需要一个例子来说明，GMM模型是最合适的。

　　在运用EM算法之前，我们首先要明确，缺失的Y取什么，这个得自己选取。那么由我们之前那篇博客，Y用来代表数据属于某个高斯分量最合适。y取1~k，分别代表k个高斯分量。那么很容易有$p(x,y=l|\pi,\mu,\Sigma) = \pi_l\mathcal{N}(x|\mu_l,\Sigma_l)$，而$p(x|\pi,\mu,\Sigma) = \sum_kp(x,y=k|\pi,\mu,\Sigma) = \sum_k\pi_k\mathcal{N}(x|\mu_k,\Sigma_k)$，这与我么GMM模型的结果也是一致的。

　　首先我们先计算$Q(\theta;\theta^{(i)})$（这里公式比较复杂，博客园的Latex比较坑，我就直接用Latex写了然后截图了）：

　　　　　　

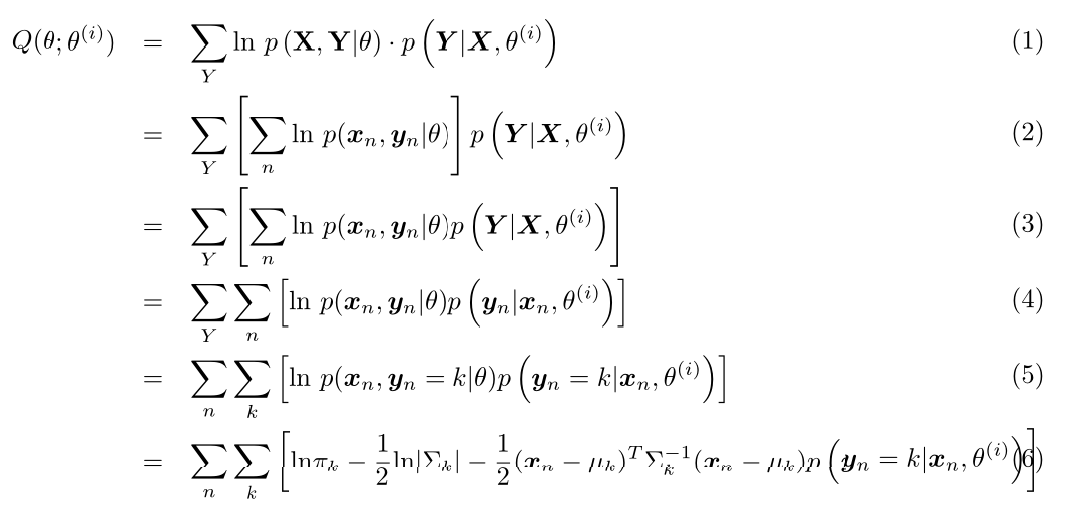
　　其中$p(\mathbf{y}_n=k|\mathbf{x}_n,\theta^{(i)}) = \frac{p(\mathbf{y}_n=k,\mathbf{x}_n|\theta^{(i)})}{p(\mathbf{x}_n|\theta^{(i)})} = \gamma_{nk}$（推导要使用本小节第二段中的两个式子，$\gamma_{nk}$定义见本系列第二篇博客）。

　　第二步，我们对$Q(\theta;\theta^{(i)})$进行最值优化，首先对均值进行求导，则有：

　　　　$\frac{\partial Q}{\partial \mu_k}=0$ 得到 $\mu_k^{(i+1)} = \frac{\sum_n\gamma_{nk}\mathbf{x}_n}{\sum_n\gamma_{nk}}$

　　细心的读者可能已经发现，这与我们在第二篇博客中得到的结果是一样的。同样，对$\pi$和$\Sigma$求导得到的结果同样和第二篇博客中一样（有兴趣的读者可以自行推导一下，其中对$\Sigma$求导可能需要参考我的另一篇博文多维高斯概率密度函数对协方差矩阵求导），这样我们就由EM算法得到了GMM的训练算法。