主成分分析(PCA)的一种直观理解

源自知乎的一个答案，网上很多关于PCA的文章，不过很多都只讲到了如何理解方差的投影，却很少有讲到为什么特征向量就是投影方向。本文从形象角度谈一谈，因为没有证明，所以不会严谨，但是应该能够帮助形象理解PCA背后的原理。

一、先从旋转和缩放角度，理解一下特征向量和特征值的几何意义

从定义来理解特征向量的话，就是经过一个矩阵变换后，空间沿着特征向量的方向上相当于只发生了缩放，比如我们考虑下面的矩阵：

\[
\begin{bmatrix}
1.5 & 0.5\\
0.5 & 1.0
\end{bmatrix}
\]

求这个变换的特征向量和特征值，分别是：\(U=\begin{bmatrix} 0.85 & -0.53\\ 0.53 & 0.85 \end{bmatrix}\)（列向量）和1.81，0.69

用一个形象的例子来说明一下几何意义，我们考虑下面笑脸图案：

为方便演示笑脸图案在0,0和1,1围起来的单位正方形里，同时也用两个箭头标出来了特征向量的方向。经过\(\begin{bmatrix} 1.5 & 0.5\\ 0.5 & 1.0 \end{bmatrix}\)变换，也就是用这个图案中的每个点的坐标和这个矩阵做乘法，得到下面图案：

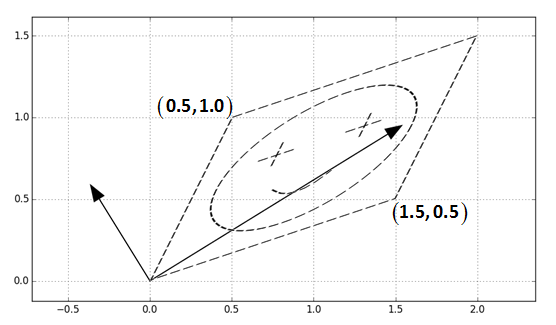
可以看到就是沿着两个正交的，特征向量的方向进行了缩放，这就是特征向量的一般的几何理解。

这个理解虽然清晰，但是并没有特别形象。我们也可以分解一下，从旋转和沿轴缩放的角度理解，分成三步：

第一步，把特征向量所指的方向分别转到横轴和纵轴这一步相当于用U的转置，也就是\(U^{T}\)进行了变换

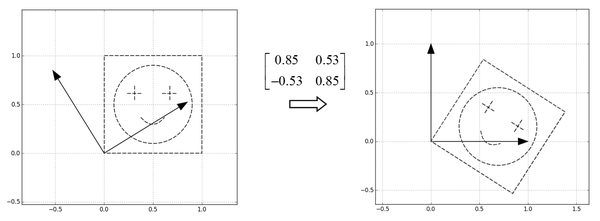
第二步，然后把特征值作为缩放倍数，构造一个缩放矩阵\(\begin{bmatrix} 1.81 & 0\\ 0 & 0.69 \end{bmatrix}\)，矩阵分别沿着横轴和纵轴进行缩放：

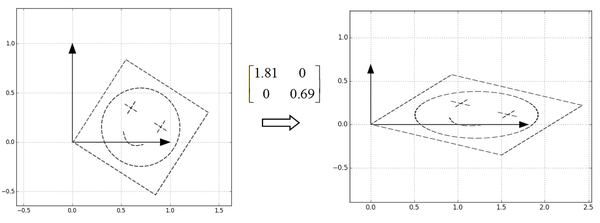
第三步，很自然地，接下来只要把这个图案转回去，也就是直接乘U就可以了

所以，从旋转和缩放的角度，一个矩阵变换就是，旋转-->沿坐标轴缩放-->转回来，的三步操作，表达如下：

\[T=U \Sigma U ^{T}\]

多提一句，这里给的是个(半)正定矩阵的例子，对于不镇定的矩阵，也是可以分解为，旋转-->沿坐标轴缩放-->旋转，的三步的，只不过最后一步和第一步的两个旋转不是转回去的关系了，表达如下：

\[T=U \Sigma V^{T}\]

这个就是SVD分解，就不详细说了。另外，这个例子是二维的，高维类似，但是形象理解需要脑补。

二、协方差矩阵的特征向量PCA的意义

一句话概括PCA的话就是找到方差在该方向上投影最大的那些方向，比如下边这个图是用\(\begin{bmatrix} 1 & 0.5\\ 0.5 & 1 \end{bmatrix}\)作为些协方差矩阵产生的高斯分布样本：

大致用个椭圆圈出来分布，相关性最强的（0.707，0.707）方向就是投影之后方差最大的方向。接下来我们不尝试严格证明，而是从旋转和缩放的角度形象理解一下，我们可以考虑把这个分布也旋转一下，让长轴在x轴上，短轴在y轴上，变成如下：

然后再沿着x轴和y轴，除以标准差，缩放成标准差为1的单位分布：

注意，在这个除以标准差的过程中，标准差最大的轴，就对应着原空间中，样本投影后方差最大的方向。接下来，假设这个分布中的样本为\(X_U\)，则我们可以把一开始的样本表示为：

\[X=ULX_U\]

用这么别扭的表示方式主要是为了接下来推公式方便，所以接下来推个简单的公式：

协方差矩阵，用S表示，则有

\[S_{ij}=E\left[ (X_i-\mu _i)(X_j-\mu _j) \right]\]

因为这个分布里两个维度的均值都是0，所以有

\[S_{ij}=E\left[ X_iX_j \right]\]

所以

\[S=\frac{1}{N} XX^T\]

其中N是样本数，根据前面的\(X=ULX_U\)，进一步展开这个公式：

\[S=\frac{1}{N} XX^T=\frac{1}{N}(ULX_U)(ULX_U)^T=UL(\frac{1}{N}X_U{X_U}^T)L^TU^T\]

因为\(X_U\)是个单位方差的且无相关性的样本，所以

\[\frac{1}{N}X_U{X_U}^T=I\]

另外L是个对角矩阵所以有

\[S=ULL^TU^T=UL^2U^T=U\Sigma U^T\]

这个公式上一部分已经说过了。所以对角线上的元素对应的就是方差的大小，而缩放倍数就是标准差的大小，也就是特征值的开根号，而U就是要沿着缩放的方向，也就是问题中投影的方向，正是特征向量。