hiho一下123周 后缀数组四·重复旋律

后缀数组四·重复旋律4

时间限制:5000ms

单点时限:1000ms

内存限制:256MB

描述

小Hi平时的一大兴趣爱好就是演奏钢琴。我们知道一个音乐旋律被表示为长度为 N 的数构成的数列。小Hi在练习过很多曲子以后发现很多作品中的旋律有重复的部分。

我们把一段旋律称为(k,l)-重复的，如果它满足由一个长度为l的字符串重复了k次组成。 如旋律abaabaabaaba是(4,3)重复的，因为它由aba重复4次组成。

小Hi想知道一部作品中k最大的(k,l)-重复旋律。

解题方法提示

输入

一行一个仅包含小写字母的字符串。字符串长度不超过 100000。

输出

一行一个整数，表示答案k。

样例输入

babbabaabaabaabab

样例输出

4
解题方法提示：

小Ho：这一次的问题该如何解决呢？

小Hi：嗯，这次的问题是重复次数最多的连续字串。

小Ho：似乎不好下手啊。

小Hi：那我们先降低难度，不如考虑如何解决如何求一个串的最大重复次数。

小Ho：嗯。我想想，比如说串abababab，既可以是(1,8)，也可以是(2,4)，最大的是(4,2)。

小Hi：对。假如说我们枚举一个可能的循环节长度l（或者k），能不能快速判断这个l是否合法呢？

小Ho：啊！我想想...似乎是求原串和原串去掉前l个字符后两个串的LCP（最长公共前缀），如果能完全匹配上，就满足！

小Hi：对，没错。比如abababab，检验是否是(2,4)，就拿abababab和ababab求LCP。

小Hi：值得一提的是，利用height数组可以快速求出我们需要的LCP。例如abababab的height数组如下：

suffix	sa	height
ab	7	0
abab	5	2
ababab	3	4
abababab	1	6
b	8	0
bab	6	1
babab	4	3
bababab	2	5

小Hi：如果我们要求某两个后缀的LCP，只要求它们中间的一段height数组的最小值即可。例如abababab和ababab的LCP就是[4]这段的最小值，即2；bab和bababab的LCP就是[3, 5]这段的最小值，即3；ab和babab的LCP就是[2, 4, 6, 0, 1, 3]这段的最小值，即0。

小Hi：这个求height数组某一段最小值的问题，恰好是之前讲过的[RMQ问题]，可以通过O(NlogN)的预处理达到O(1),处理单次询问；当然使用线段树等数据结构也是可以的，单次询问O(logN)。

小Ho：明白了。回到原问题，那我们肯定是要先枚举(k,l)中的这个l，再枚举起始位置i，计算Suffix(i)和Suffix(i+l)的LCP，记作lcp(l, i)，那么k(l, i)就等于lcp(l,i)/l + 1。对于所有的循环节长度l和起始位置i，最大的k(l, i)就是答案。

小Hi：你说的对！不过本题还是有进一步优化的空间。对于确定的l，我们不用枚举所有的起始位置i，而只枚举i是l的整数倍的情况。如果最优串的开始位置恰好在l的倍数上，那我们找到的最大的k就是正确答案。

小Ho：道理是这么个道理。不过如果最优串的开始位置不在l的倍数上呢？

小Hi：即使不是，问题也会太糟糕，假如说最优串位置在x，可以想象我们会枚举到x之后的一个最近位置p，p是l的倍数。并且我们计算出了Suffix(p)和Suffix(p+l)的LCP，lcp(l, p)那么此时的k(l, p)=lcp(l, p)/l+1。

小Hi：对于被我们略过的k(l, p-1), k(l, p-2) ... k(l, p-l+1)，它们的上限是k(l, p)+1。

小Ho：没错。因为它们的起始位置距离p不超过l，所以最多比Suffix(p)增加一个循环节。

小Hi：其次，如果k(l, p-1), k(l, p-2) ... k(l, p-l+1)中有一个的值是k(l, p)+1的话，那么k(l, p - l + lcp(l, p) mod l)一定等于k(l, p)+1。(mod是取余运算)

小HO：为什么呢？

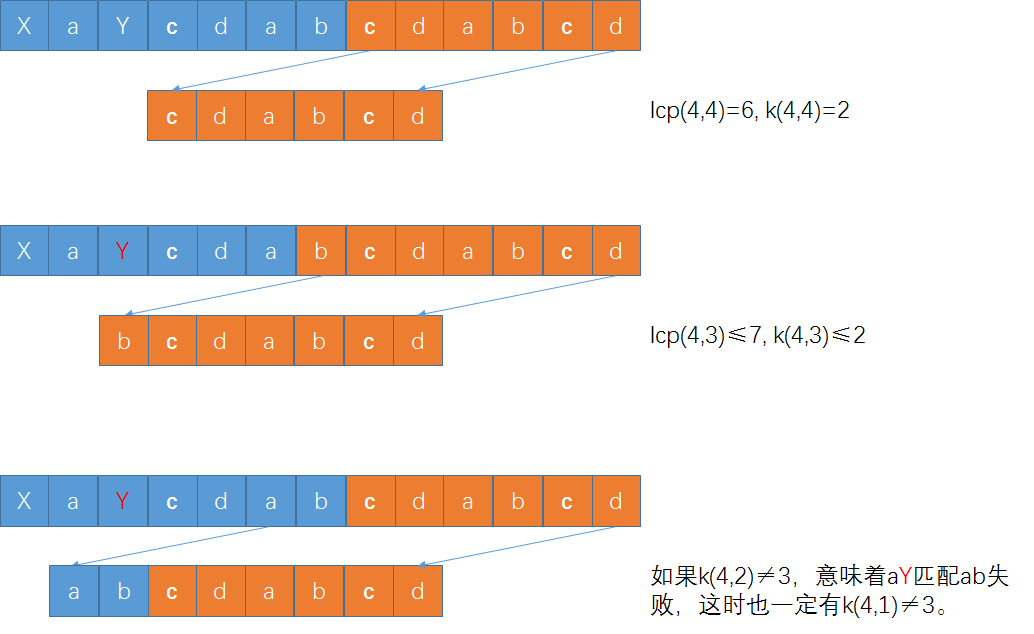
小Hi：举个例子，比如串XaYcdabcdabcd(XY各代表一个不确定的字符，具体代表的字符会影响最后答案，我们后面会分析到)，当我们考虑l=4的时候，第一次枚举p=4的起始位置，会求出cdabcdabcd和cdabcd的lcp(4, 4)=6，k(4, 4)=2。根据上面的论断，只有当k(l, p - l + lcp(l, p) mod l)=k(4, 4 - 4 + 6 mod 4)=k(4, 2)=3时，k(4, 1), k(4, 2)和k(4, 3)中才会有3。首先我们可以判断k(4, 3)一定不可能等于3，因为无论Y是哪个字符，Ycdabcdabcd和bcdabcd的LCP即lcp(4, 3)最大是7，不到8。 其次如果k(4, 2) ≠ 3，那么k(4, 1)也没戏。因为如果k(4, 2) ≠ 3，说明aY和ab匹配不上，这时无论X是哪个字符，XaY和dab匹配不上，lcp(4, 1) < l，k(4, 1) = 1。

小Ho：哦，我有点明白了。k(l, p - l + lcp(l, p) mod l)是一个分界线，右边的值因为LCP不够大，一定不能增加一个循环节。并且如果k(l, p - l + lcp(l, p) mod l)没有增加循环节的话，说明[p - l + lcp(l, p) mod l, p]这段中间匹配出错，左边的lcp也跟着雪崩，更不可能增加循环节了。

小Hi：没错！

小Ho：那枚举l和枚举开始位置的时间复杂度呢？

小Hi：你会发现，枚举完l后枚举开始位置的时间复杂度是O(n/l)的，所以总复杂度是O(n/1)+O(n/2)+O(n/3)...这个是一个经典的求和，总复杂度是O(nlogn)的。

小Ho：明白了！好神奇，看似简单朴素的想法，复杂度却也很低。

小Hi：是啊。以下是二分判断的C++代码实现：

for(L＝1;L <= n;L++)
{
    for (int i = 1; i + L <= n; i += L)
    {
        int R = lcp(i, i + L);
        ans = max(ans, R / L + 1);
        if (i >= L - R % L)
        {
            ans = max(lcp(i - L + R%L, i + R%L) / L + 1, ans);
        }
    }
}

小Ho：好的。我这就实现一下。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#define inf 2e9
#define met(a,b) memset(a,b,sizeof a)
typedef long long ll;
using namespace std;
const int N = 2e5+;
const int M = 4e5+;
int cmp(int *r,int a,int b,int l)
{
    return (r[a]==r[b]) && (r[a+l]==r[b+l]);
}

int wa[N],wb[N],wss[N],wv[N];
int Rank[N];//后缀i在sa[]中的排名
int height[N];//sa[i]与sa[i-1]的LCP
int sa[N];//sa[i]表示排名第i小的后缀的下标
void DA(int *r,int *sa,int n,int m)  //此处N比输入的N要多1，为人工添加的一个字符，用于避免CMP时越界
{
    int i,j,p,*x=wa,*y=wb,*t;
    for(i=; i<m; i++) wss[i]=;
    for(i=; i<n; i++) wss[x[i]=r[i]]++;
    for(i=; i<m; i++) wss[i]+=wss[i-];
    for(i=n-; i>=; i--) sa[--wss[x[i]]]=i; //预处理长度为1
    for(j=,p=; p<n; j*=,m=p) //通过已经求出的长度J的SA，来求2*J的SA
    {
        for(p=,i=n-j; i<n; i++) y[p++]=i; // 特殊处理没有第二关键字的
        for(i=; i<n; i++) if(sa[i]>=j) y[p++]=sa[i]-j; //利用长度J的，按第二关键字排序
        for(i=; i<n; i++) wv[i]=x[y[i]];
        for(i=; i<m; i++) wss[i]=;
        for(i=; i<n; i++) wss[wv[i]]++;
        for(i=; i<m; i++) wss[i]+=wss[i-];
        for(i=n-; i>=; i--) sa[--wss[wv[i]]]=y[i]; //基数排序部分
        for(t=x,x=y,y=t,p=,x[sa[]]=,i=; i<n; i++)
            x[sa[i]]=cmp(y,sa[i-],sa[i],j)?p-:p++;  //更新名次数组x[],注意判定相同的
    }
}

void calheight(int *r,int n)  // 此处N为实际长度
{
    int i,j,k=;        // height[]的合法范围为 1-N, 其中0是结尾加入的字符
    for(i=; i<=n; i++) Rank[sa[i]]=i; // 根据SA求Rank
    for(i=; i<n; height[Rank[i++]] = k ) // 定义：h[i] = height[ Rank[i] ]
    for(k?k--:,j=sa[Rank[i]-]; r[i+k]==r[j+k]; k++); //根据 h[i] >= h[i-1]-1 来优化计算height过程
}
int n;
char ss[N];
int aa[N];
const int maxn=N;
int mn[N][];
int log22[N];
void pre()
{
    for (int i=; i<=n; i++)
        log22[i]=log2(i);
}
void rmq_init(int n,int *h)
{
    for (int j=; j<=n; j++) mn[j][]=h[j];
    int m=log22[n];
    for (int i=; i<=m; i++)
        for (int j=n; j>; j--)
        {
            mn[j][i]=mn[j][i-];
            if ( j+(<<(i-)) <=n ) mn[j][i]=min(mn[j][i], mn[j+(<<(i-)) ] [i-]);
        }
}
int lcp_min(int l,int r) //求lcp(l,r)
{
    if (l>r)swap(l,r);  //先交换
    l++;                //根据height定义，l++
    int m=log22[r-l+];
    return min(mn[l][m],mn[r-(<<m)+][m]);
}

int solve()
{
    int ans=;
    for (int  L=; L<=n; L++)
    {
        for (int j=; j<n; j+=L)
        {
            int lcp_len=lcp_min( Rank[j],Rank[j+L]);
            ans=max(ans,lcp_len/L+);
            int last_possible_pos=j-(L-lcp_len%L);
            if (last_possible_pos>=)
                ans=max(ans, +lcp_min( Rank[last_possible_pos] ,Rank[last_possible_pos+L]   )/L  ) ;
        }
    }
    return ans;
}

int main ()
{
    scanf("%s",&ss);
    n=strlen(ss);
    for (int i=; i<n; i++)aa[i]=ss[i]-'a'+;
    aa[n]=;
    DA(aa,sa,n+,);
    calheight(aa,n);
    pre();
    rmq_init(n,height);
    int ans= solve();
    printf("%d\n",ans);
    return ;
}