中心极限定理|z分布|t分布|卡方分布

生物统计学

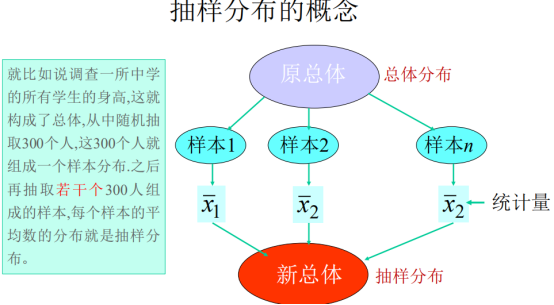
抽样分布：n个样本会得到n个统计量，将这n个统计量作为总体，该总体的分布即是抽样分布

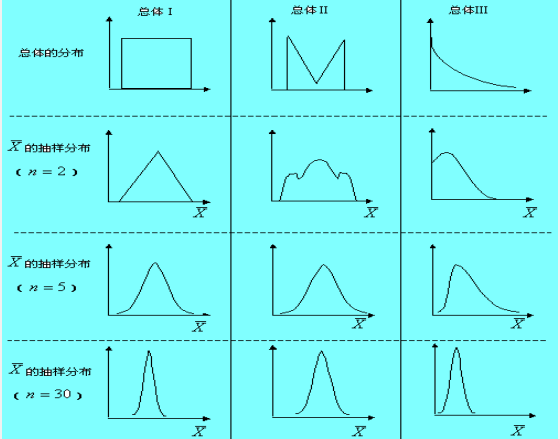
根据辛钦大数定律，从一个非正态分布的总体中抽取的含量主n的样本，当n充分大时，样本平均数渐近服从正态分布。因此平均数的抽样分布对正态性的要求并不是十分严格，但方差的抽样分布，对总体的正态性的要求是十分严格的。

样本平均值的分布：

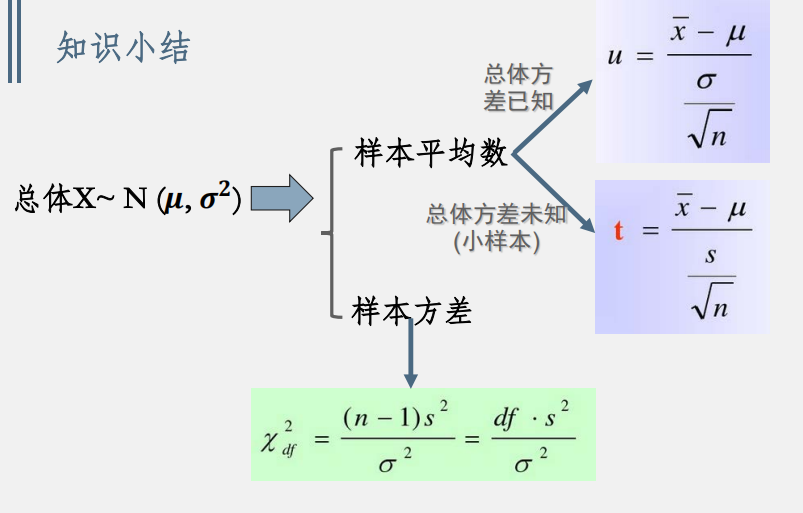
基于正态总体(两个参数都知道)的抽样分布:

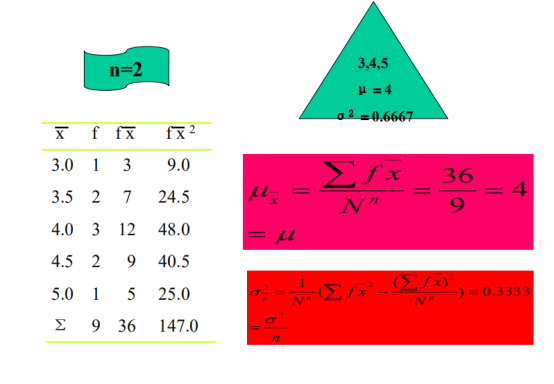
eg'：总体n=3,

因为n=2有放回抽样,有9种可能性：

n=4有放回抽样,有81种可能性

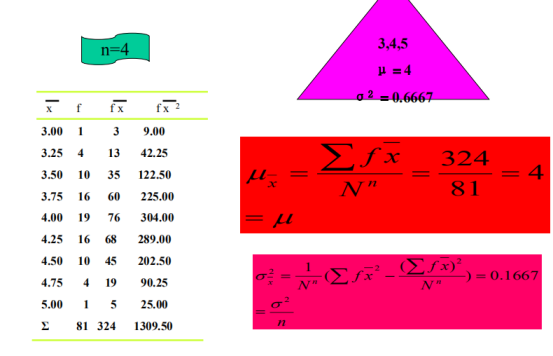
统计量与总体参数不完全一样，但是满足以上关系，所以有：

标准误就是参数方差

非正态分布总体(两个参数都知道)：根据中心极限定理，大样本同基于正态总体

所以，只要是大样本都会满足z分布，z即满足N(0,1)

方差未知：用样本标准差代替总体标准差，并得到t,此时是t满足自由度为（n-1）的t分布，从PDF可知t分布只与自由度有关，与其他无关。

因为n个数要满足均数，必有一个数的值受其他数影响，又因为自由度是独立观测的个数，所以自由度为n-1：

当自由度较大时，也就是n较大时就是正态分布；t--->u

特征值：

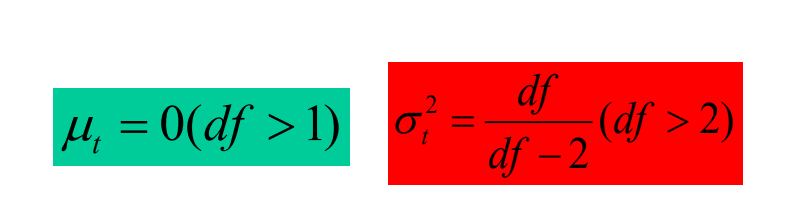
总体分布和抽样分布的关系：

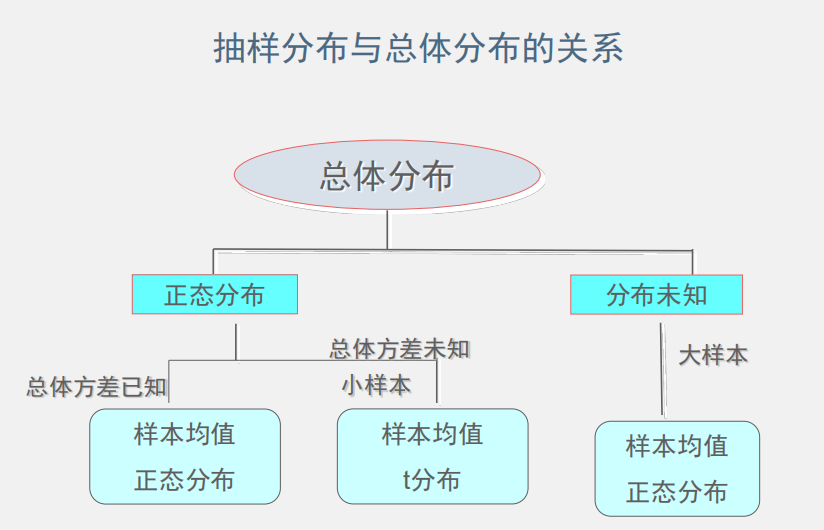
PS：对于总体分布未知的小样本并无方法

样本方差的分布

正态总体时，两个参数都知道的情况下，样本方差满足卡方分布

随机变量是S方，所以卡方也是一个随机变量，卡方分布只与自由度有关系。

总结：

两个正态分布总体（都知道均数和方差），两个样本平均数的和与差的分布：利用正态分布加加减减

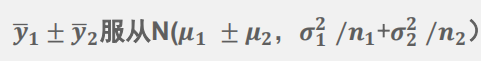
两个正态分布总体（都知道均数，但未知方差具体值，但知道方差相等），两个样本平均数的和与差的分布：利用他分布加加减减

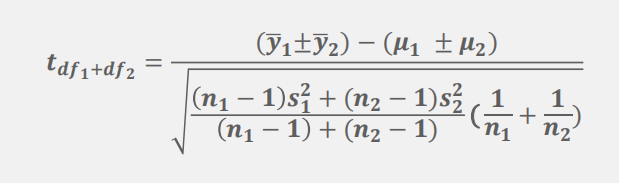
分布使用条件：1.均值是否已知？2.方差是否已知？3.样本量是大或者小？