luogu P2766 最长不下降子序列问题

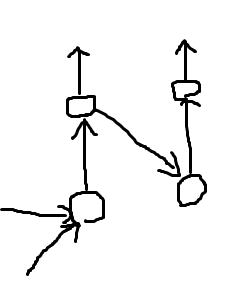
第一问可以直接DP来做，联想上一题，线性规划都可以化为网络流？我们可以借助第一问的DP数组，来建立第二问第三问的网络流图，考虑每一种可能，都是dp数组中满足num[i]>=num[j]&&dp[i]=dp[j]+1(i>j)，每一种可能都是从dp为1的点递增到dp为第一问的值的点，那么我们就设一个源点一个汇点，每个源点向dp为1的点连capacity为1的边，每个dp为第一问答案的点向汇点连capacity为1的边，每一个满足dp条件，即num[i]>=num[j]&&dp[i]=dp[j]+1(i>j)，从j向i连一条capacity为1的边，跑最大流即可，但是，我们注意到，题目要求是不同的，不重复的，而我们的做法无法考虑一个点是否重复使用，举个例子(丑图上

在这种情况下，第一个节点重复使用了，显然不满足题意，那我们怎么做呢，要满足不重复的条件，可以把每个点拆成入点和出点，入点向出点连一条capacity为1的边，就能完美的保证每个点只使用一次啦，相同情况如下，能保证只使用一次

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) ((x)&(-x))
typedef long long LL;

const int maxm = 3e3+;
const int INF = 0x3f3f3f3f;

struct edge{
    int u, v, cap, flow, nex;
} edges[maxm];

int head[maxm], cur[maxm], cnt, level[], buf[], dp[];

void init() {
    memset(head, -, sizeof(head));cnt = ;
}

void add(int u, int v, int cap) {
    edges[cnt] = edge{u, v, cap, , head[u]};
    head[u] = cnt++;
}

void addedge(int u, int v, int cap) {
    add(u, v, cap), add(v, u, );
}

void bfs(int s) {
    memset(level, -, sizeof(level));
    queue<int> q;
    level[s] = ;
    q.push(s);
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        for(int i = head[u]; i != -; i = edges[i].nex) {
            edge& now = edges[i];
            if(now.cap > now.flow && level[now.v] < ) {
                level[now.v] = level[u] + ;
                q.push(now.v);
            }
        }
    }
}

int dfs(int u, int t, int f) {
    if(u == t) return f;
    for(int& i = cur[u]; i != -; i = edges[i].nex) {
        edge& now = edges[i];
        if(now.cap > now.flow && level[u] < level[now.v]) {
            int d = dfs(now.v, t, min(f, now.cap - now.flow));
            if(d > ) {
                now.flow += d;
                edges[i^].flow -= d;
                return d;
            }

        }
    }
    return ;
}

int dinic(int s, int t) {
    int maxflow = ;
    for(;;) {
        bfs(s);
        if(level[t] < ) break;
        memcpy(cur, head, sizeof(head));
        int f;
        while((f = dfs(s, t, INF)) > )
            maxflow += f;
    }
    return maxflow;
}

void run_case() {
    int n;
    init();
    cin >> n;
    int s = , t = (n<<)+;
    for(int i = ; i <= n; ++i) {
        cin >> buf[i];
        dp[i] = ;
    }
    for(int i = ; i <= n; ++i)
        for(int j = ; j < i; ++j)
            if(buf[i] >= buf[j])
                dp[i] = max(dp[i], dp[j] + );
    int ans = ;
    for(int i = ; i <= n; ++i) ans = max(ans, dp[i]);
    cout << ans << "\n";
    for(int i = ; i <= n; ++i) {
        for(int j = ; j < i; ++j) {
            if(buf[i] >= buf[j] && dp[i] == dp[j]+) addedge((j<<)|, i<<, );
        }
        addedge(i<<, (i<<)|, );
        if(dp[i] == ) addedge(s, i<<, );
        if(dp[i] == ans) addedge((i<<)|, t, );

    }
    int sum = dinic(s, t);
    cout << sum << "\n";
    addedge(, , INF), addedge(n<<, (n<<)|, INF);
    if(dp[] == ) addedge(s, , INF);
    if(dp[n] == ans) addedge((n<<)|, t, INF);
    int threequestion = dinic(s, t);
    sum += threequestion==INF?:threequestion;
    cout << sum << "\n";

}

int main() {
    ios::sync_with_stdio(false), cin.tie();
    run_case();
    cout.flush();
    return ;
}