支持向量机(SVM)（三）-- 最优间隔分类器（optimal margin classifier）

在之前为了寻找最有分类器，我们提出了例如以下优化问题：

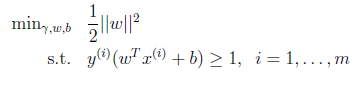
在这里我们能够把约束条件改写成例如以下：

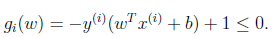
首先我们看以下的图示：

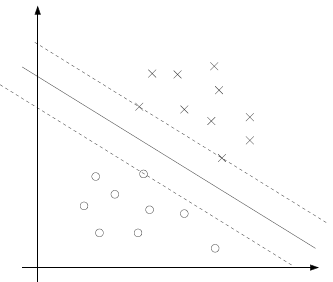
非常显然我们能够看出实线是最大间隔超平面，如果×号的是正例，圆圈的是负例。在虚线上的点和在实线上面的两个一共这三个点称作支持向量。如今我们结合KKT条件分析下这个图。

我们从式子和式子能够看出假设那么，

这个也就说明时。w处于可行域的边界上，这时才是起作用的约束。

1、那我们如今能够构造拉格朗日函数例如以下：

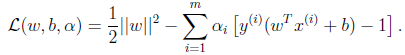
注意到这里仅仅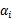有没有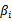是由于原问题中没有等式约束，仅仅有不等式约束。

2、接下来我们对w和b分别求偏导数。

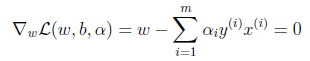
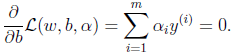
并得到

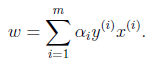
3、将上式带回到拉格朗日函数中得到：

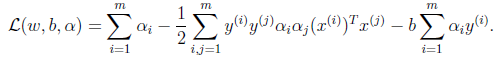
因为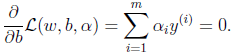，因此简化为

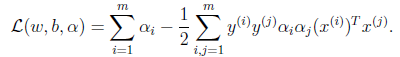
4、如今我们得到了关于w和b的能够最小化的等式。我们在联合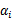这个參数，当然他的条件还是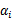>=0，如今我们能够得到例如以下的二元优化等式了：

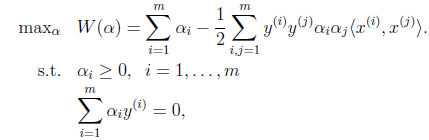
5、如今你还必须知道我们之前解说的条件一是，二是KKT条件：

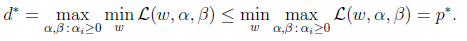
非常显然存在w使得对于全部的i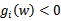，。因此，一定存在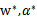使得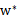是原问题的解。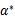是对偶问题的解。

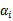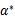假设求出了（也就是），依据

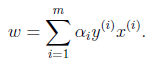
就可以求出w（也是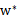，原问题的解）。然后

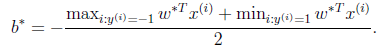
就可以求出b。即离超平面近期的正的函数间隔要等于离超平面近期的负的函数间隔。

6、如今我们在看另外一个问题：

因为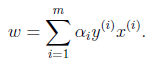

所以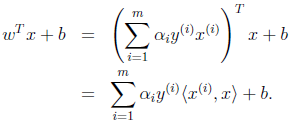

这里我们将向量内积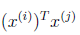表示为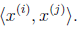

如今能够看出我要计算等式的话就仅仅须要计算向量的内积就好了。同一时候要是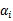 在支持向量上面的话。那么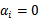，这样就更简单了，因此非常多的值都是0。