Dijkstra算法分析

题目分析参照《数据结构》(严蔚敏)7-6节

最短路径问题描述

参照日常生活中的公交查询系统。我们有选项：

少换乘/最少站数

价格最少/时间最短....

（ps:下边这个图是网页查询的，略有出入）

根据这样的分类。我们可以将最短路径分为：结点最少(经过的站数最少)，权值最小（这个就是个心里期望了，看你是相花费时间最少，金钱最少....）

结点最少

（参照途中描述）

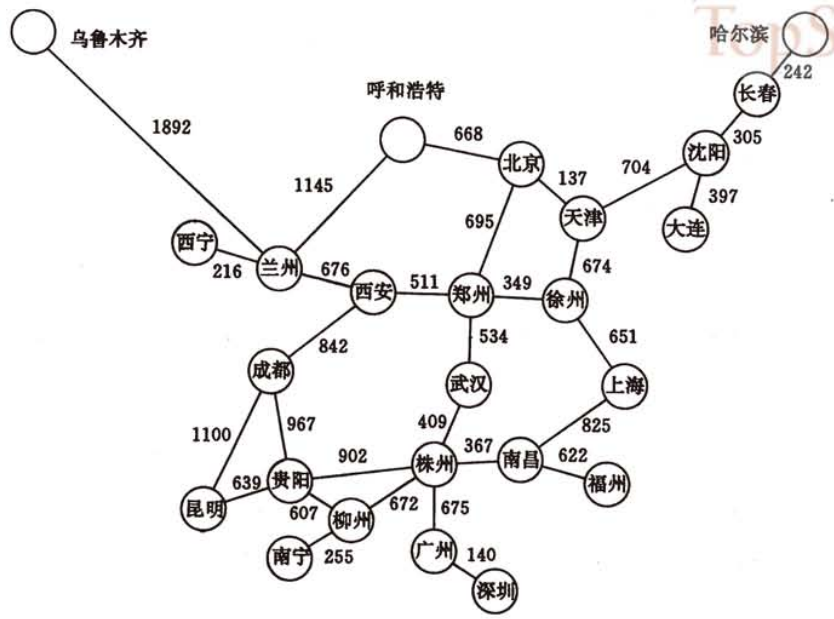
由此可以看出，对于经过站点最少，换乘最少这种问题，我们只需要对图进行广度遍历，即可获取相关结果。

我们重点分析下面的情况

权值最小（花费最少）

理论：从A到B，他们之间的路径要么是A->B,要么经过中间节点  A->..->B其最短路径也就是两条路径中最短的一条。

于是有：对于最短路径问题，我们只需要利用动态规划，在遍历中更新，逐步获取最短路径。

具体分析图如下

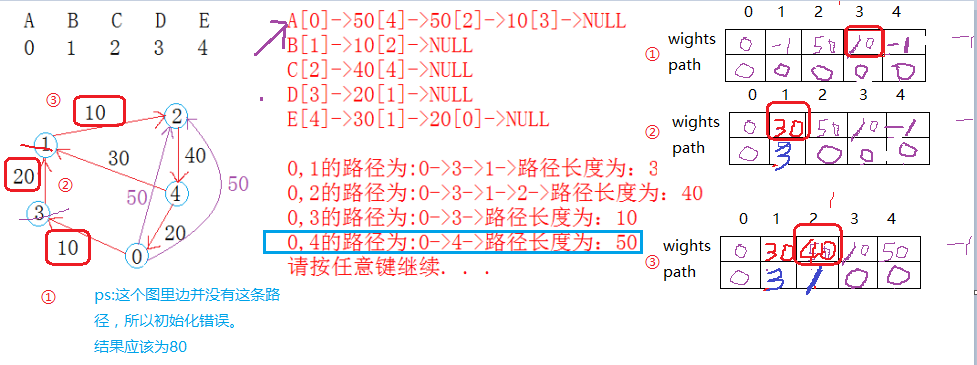
如上为寻找下标0-2结点过程的分析。对应代码

  1.     bool Dijkstra(const V&src,const V&dst,int &ret)
  2.     {
  3.         //如果只有顶点，那么返回true，ret =0；
  4.         if (_size <= )
  5.         {
  6.             ret = ;
  7.             return true;
  8.         }
  9.         int cur = FindIndexV(src);
  10.         int end = FindIndexV(dst);
  11.  
  12.         int beg = cur;
  13.  
  14.         size_t wights[] = {};
  15.         int paths[] = {};
  16.         for (size_t i = ; i < _size; ++i)
  17.         {
  18.             wights[i] = -;
  19.             paths[i] = src;
  20.         }
  21.         wights[cur] = ;
  22.         paths[cur] = ;
  23.  
  24.         Edge* pcur = _eList[cur];
  25.         //首次更新
  26.         while (pcur)
  27.         {
  28.             wights[pcur->_dst] = pcur->_wight;
  29.             pcur = pcur->_next;
  30.         }
  31.         pcur = _eList[cur];
  32.  
  33.         int visitedCount = ;
  34.         while (cur!=end)//未走到目的
  35.         {
  36.             if (cur == beg)
  37.                 visitedCount++;
  38.             //如果起点没有路径且目标不可达//或者回到起点了
  39.             if (pcur == NULL&&wights[dst] == -||cur == beg&&visitedCount==)
  40.             {
  41.                 return false;
  42.             }
  43.  
  44.             //获取最短边
  45.             Edge* minCur = _eList[cur];
  46.             Edge* pcur = _eList[cur];
  47.             while (pcur)
  48.             {
  49.                 if (minCur->_wight > pcur->_wight)
  50.                     minCur = pcur;
  51.                 pcur = pcur->_next;
  52.             }
  53.             cur = minCur->_src;
  54.             //根据局部最短更新路径
  55.             if (wights[cur] + minCur->_wight < wights[minCur->_dst])
  56.             {
  57.                 wights[minCur->_dst] = wights[cur] + minCur->_wight;
  58.                 paths[minCur->_dst] = minCur->_src;
  59.             }
  60.  
  61.             cur = minCur->_dst;
  62.             if (minCur->_dst == FindIndexV(dst))
  63.             {
  64.                 ret = wights[minCur->_dst];
  65.                 return true;
  66.             }
  67.         }
  68.     }

以下是整个图项目文件以及对应于最短路径的测试用例

  1. #pragma once
  2. //邻接表实现图
  3.  
  4. #include<queue>
  5. #include<stack>
  6. #include"UnionFindset.h"
  7.  
  8. #include<map>
  9. template<class V, class E>
  10. struct Edge
  11. {
  12.     Edge(size_t dst,size_t src, const E&e)
  13.         :_wight(e)
  14.         ,_dst(dst)
  15.         ,_src(src)
  16.         , _next(NULL)
  17.     {}
  18.     E _wight;       //权值，边比重
  19.     size_t _dst;    //目的顶点下标
  20.     size_t _src;    //源顶点下标
  21.     struct Edge<V, E>* _next;
  22.  
  23.     bool operator<(const Edge* &ed)
  24.     {
  25.         return _wight < ed->_wight;
  26.     }
  27. };
  28.  
  29. template<class V,class E>
  30. class GraphList
  31. {
  32.     typedef Edge<V, E> Edge;
  33. protected:
  34.     V* _vArr;               //顶点存储数组
  35.     size_t _size;
  36.  
  37.     Edge** _eList;    //边存储指针数组
  38.  
  39. public:
  40.     GraphList(const V* vArray, const size_t size)
  41.         :_size(size)
  42.         , _vArr(new V[size])
  43.     {
  44.         //初始化顶点保存
  45.         for (size_t i = ; i < size; ++i)
  46.         {
  47.             _vArr[i] = vArray[i];
  48.         }
  49.         //初始化边结构
  50.         _eList = new Edge*[size];
  51.         memset(_eList, , sizeof(Edge*)*size);
  52.     }
  53.  
  54.     int FindIndexV(const V& v) const
  55.     {
  56.         for (size_t i = ; i < _size; ++i)
  57.         {
  58.             if (_vArr[i] == v)
  59.                 return i;
  60.         }
  61.         return -;
  62.     }
  63.  
  64.     //添加v1->v2的边
  65.     void AddEdge2(const V& v1, const V&v2, const E& e, bool IsDir = true)
  66.     {
  67.         int ind1 = FindIndexV(v1);
  68.         int ind2 = FindIndexV(v2);
  69.  
  70.         Edge* cur = new Edge(ind2, ind1, e);
  71.  
  72.         cur->_next = _eList[ind1];
  73.         _eList[ind1] = cur;
  74.  
  75.         if (!IsDir)
  76.         {
  77.             Edge* cur = new Edge(ind1, ind2, e);
  78.             cur->_next = _eList[ind2];
  79.             _eList[ind2] = cur;
  80.         }
  81.  
  82.     }
  83.  
  84.     void Display()const
  85.     {
  86.         cout << "顶点集合" << endl;
  87.         for (size_t i = ; i < _size; ++i)
  88.         {
  89.             cout << _vArr[i] << " ";
  90.         }
  91.         cout << endl << "边表示" << endl;
  92.  
  93.         for (size_t i = ; i < _size; ++i)
  94.         {
  95.             cout << "边["<<i << "]>>";
  96.             Edge* cur = _eList[i];
  97.             while (cur)
  98.             {
  99.                 //cout << "[" << cur->_dst << "]" << cur->_wight << " ";
  100.                 //printf("[%d]:", cur->_dst, cur->_wight);
  101.                 cout << "[" << cur->_dst << "]" << cur->_wight << "--> ";
  102.                 cur = cur->_next;
  103.             }
  104.             cout <<"NULL"<< endl;
  105.         }
  106.         cout << endl;
  107.     }
  108.  
  109.     //广度优先
  110.     void BSP(const V& root)
  111.     {
  112.         cout << "广度优先遍历：" << endl;
  113.         bool *visited = new bool[_size]();
  114.  
  115.         queue<int> q;
  116.         int index = FindIndexV(root);
  117.  
  118.         q.push(index);
  119.  
  120.         while (!q.empty())
  121.         {
  122.             index = q.front();
  123.             if (visited[index] == false)
  124.             {
  125.                 cout << _vArr[index]<<"-->";
  126.             }
  127.  
  128.             visited[index] = true;
  129.  
  130.             q.pop();
  131.             Edge* cur = _eList[index];
  132.             while (cur)
  133.             {
  134.                 if (visited[cur->_dst] == false)//未访问过那么压入
  135.                 {
  136.                     q.push(cur->_dst);
  137.                 }
  138.                 cur = cur->_next;
  139.             }
  140.         }
  141.         cout << endl << endl;
  142.     }
  143.  
  144.     //深度优先
  145.     void DSP(const V& root)
  146.     {
  147.         //
  148.         cout << "深度优先遍历：" << endl;
  149.         _DSP(root);
  150.         cout << endl << endl;
  151.     }
  152.     void _DSP(const V& root)
  153.     {
  154.         static bool *visited = new bool[_size]();
  155.         int index = FindIndexV(root);
  156.         if (visited[index] == false)
  157.         {
  158.             cout << _vArr[index] << "-->";
  159.             visited[index] = true;
  160.         }
  161.  
  162.         Edge* cur = _eList[index];
  163.  
  164.         while (cur)
  165.         {
  166.             if (visited[cur->_dst] == false)
  167.                 _DSP(_vArr[cur->_dst]);
  168.             cur = cur->_next;
  169.         }
  170.         if (cur == NULL)
  171.             return;
  172.     }
  173.  
  174.     //在所有边中获取最小权值的边
  175.     int FindMinEdgeIndex(vector<Edge*>&v)
  176.     {
  177.         int min = ;
  178.         for (size_t i = ; i < v.size(); ++i)
  179.         {
  180.             if (v[i]->_wight < v[min]->_wight)
  181.                 min = i;
  182.         }
  183.         return min;
  184.     }
  185.  
  186.     bool Kruskal(GraphList<V,E>& minTree)
  187.     {
  188.         vector<Edge*> ve;
  189.         for (size_t i = ; i < _size; ++i)
  190.         {
  191.             Edge* cur = _eList[i];
  192.             while (cur)
  193.             {
  194.                 //只插入有效边
  195.                 ve.push_back(cur);
  196.                 cur = cur->_next;
  197.             }
  198.         }
  199.  
  200.         UnionFindSet us(_size);
  201.  
  202.         while (!ve.empty())
  203.         {
  204.             //找到最小权值边
  205.             int i = FindMinEdgeIndex(ve);
  206.             //并查集插入相关结点
  207.             bool sure = us.Combine(ve[i]->_src, ve[i]->_dst);
  208.             if (sure)   //如果不是连通的，那么加入该边
  209.             {
  210.                 minTree.AddEdge2(_vArr[ve[i]->_src], _vArr[ve[i]->_dst], ve[i]->_wight);
  211.             }
  212.             ve.erase(ve.begin()+i);
  213.         }
  214.  
  215.         return us.IsOnlyOneRoot();
  216.     }
  217.  
  218.     //在相关边中获取最小权值的边
  219.     int FindMinEdgeIndexByInGraph(vector<Edge*>&v,vector<int>& nodes)
  220.     {
  221.         if (nodes.size() == )
  222.             return FindMinEdgeIndex(v);
  223.         int min = -;
  224.         for (size_t i = ; i < v.size(); ++i)   //遍历所有结点
  225.         {
  226.             //如果
  227.  
  228.             if (v[i]->_wight < v[min]->_wight)
  229.             {
  230.                 bool inNodes = false;
  231.                 for (size_t j = ; j < nodes.size(); ++i)
  232.                 {
  233.                     if (v[i]->_dst == nodes[j] || v[i]->_src == nodes[j])
  234.                     {
  235.                         inNodes = true;
  236.                         break;
  237.                     }
  238.                 }
  239.                 if(inNodes)
  240.                     min = i;
  241.             }      
  242.  
  243.         }
  244.         return min;
  245.     }
  246.     bool Prim(GraphList<V, E>& minTree)
  247.     {
  248.         vector<Edge*> ve;
  249.         vector<int> inGraph;
  250.         for (size_t i = ; i < _size; ++i)
  251.         {
  252.             Edge* cur = _eList[i];
  253.             while (cur)
  254.             {
  255.                 //只插入有效边
  256.                 ve.push_back(cur);
  257.                 cur = cur->_next;
  258.             }
  259.         }
  260.  
  261.         UnionFindSet us(_size);
  262.  
  263.         while (!ve.empty())
  264.         {
  265.             //找到最小权值边
  266.             int i = FindMinEdgeIndexByInGraph(ve,inGraph);
  267.             if (us.IsOnlyOneRoot())
  268.                 return true;
  269.  
  270.             else if (i == - && !us.IsOnlyOneRoot())
  271.                 return false;
  272.  
  273.             //并查集插入相关结点
  274.             bool sure = us.Combine(ve[i]->_src, ve[i]->_dst);
  275.             if (sure)   //如果不是连通的，那么加入该边
  276.             {
  277.                 minTree.AddEdge2(_vArr[ve[i]->_src], _vArr[ve[i]->_dst], ve[i]->_wight);
  278.             }
  279.             ve.erase(ve.begin() + i);
  280.         }
  281.  
  282.         return us.IsOnlyOneRoot();
  283.     }
  284.     //size_t wights[6] = {};
  285.     //int paths[6] = {};
  286.     bool Dijkstra(const V&src,const V&dst,int &ret)
  287.     {
  288.         //如果只有顶点，那么返回true，ret =0；
  289.         if (_size <= )
  290.         {
  291.             ret = ;
  292.             return true;
  293.         }
  294.         int cur = FindIndexV(src);
  295.         int end = FindIndexV(dst);
  296.  
  297.         int beg = cur;
  298.  
  299.         size_t wights[] = {};
  300.         int paths[] = {};
  301.         for (size_t i = ; i < _size; ++i)
  302.         {
  303.             wights[i] = -;
  304.             paths[i] = src;
  305.         }
  306.         wights[cur] = ;
  307.         paths[cur] = ;
  308.  
  309.         Edge* pcur = _eList[cur];
  310.         //首次更新
  311.         while (pcur)
  312.         {
  313.             wights[pcur->_dst] = pcur->_wight;
  314.             pcur = pcur->_next;
  315.         }
  316.         pcur = _eList[cur];
  317.  
  318.         int visitedCount = ;
  319.         while (cur!=end)//未走到目的
  320.         {
  321.             if (cur == beg)
  322.                 visitedCount++;
  323.             //如果起点没有路径且目标不可达//或者回到起点了
  324.             if (pcur == NULL&&wights[dst] == -||cur == beg&&visitedCount==)
  325.             {
  326.                 return false;
  327.             }
  328.  
  329.             //获取最短边
  330.             Edge* minCur = _eList[cur];
  331.             Edge* pcur = _eList[cur];
  332.             while (pcur)
  333.             {
  334.                 if (minCur->_wight > pcur->_wight)
  335.                     minCur = pcur;
  336.                 pcur = pcur->_next;
  337.             }
  338.             cur = minCur->_src;
  339.             //根据局部最短更新路径
  340.             if (wights[cur] + minCur->_wight < wights[minCur->_dst])
  341.             {
  342.                 wights[minCur->_dst] = wights[cur] + minCur->_wight;
  343.                 paths[minCur->_dst] = minCur->_src;
  344.             }
  345.  
  346.             cur = minCur->_dst;
  347.             if (minCur->_dst == FindIndexV(dst))
  348.             {
  349.                 ret = wights[minCur->_dst];
  350.                 return true;
  351.             }
  352.         }
  353.     }
  354.  
  355.     ~GraphList()
  356.     {
  357.         if (_vArr)
  358.         {
  359.             delete[]_vArr;
  360.             _vArr = NULL;
  361.         }
  362.         if (_eList)
  363.         {
  364.             for (size_t i = ; i < _size;++i)
  365.             {
  366.                 while (_eList[i] != NULL)
  367.                 {
  368.                     Edge* del = _eList[i];
  369.                     _eList[i] = del->_next;
  370.                     delete del;
  371.                     del = NULL;
  372.                 }
  373.             }
  374.         }
  375.     }
  376. };
  377.  
  378. void testD()
  379. {
  380.     //int vArr1[] = { 1,2,3,4,5,6,7,8,9 };
  381.     //GraphList<int, int> gh1(vArr1, sizeof(vArr1) / sizeof(vArr1[0]));
  382.  
  383.     //gh1.AddEdge2(1, 2, 11);
  384.     //gh1.AddEdge2(1, 3, 33);
  385.     //gh1.AddEdge2(1, 5, 33);
  386.     //gh1.AddEdge2(2, 3, 33);
  387.     //gh1.AddEdge2(2, 6, 99);
  388.     //gh1.AddEdge2(5, 3, 33);
  389.     //gh1.AddEdge2(3, 4, 44);
  390.     //gh1.AddEdge2(4, 5, 55);
  391.     //gh1.AddEdge2(4, 7, 32);
  392.     //gh1.AddEdge2(7, 8, 65);
  393.     //gh1.AddEdge2(1, 9, 12);
  394.     //gh1.AddEdge2(9, 7, 22);    
  395.  
  396.     int vArr1[] = { ,,,,,};
  397.     GraphList<int, int> gh1(vArr1, sizeof(vArr1) / sizeof(vArr1[]));
  398.  
  399.     gh1.AddEdge2(, , );
  400.     gh1.AddEdge2(, , );
  401.     gh1.AddEdge2(, , );
  402.     gh1.AddEdge2(, , );
  403.     gh1.AddEdge2(, , );
  404.     gh1.AddEdge2(, , );
  405.     gh1.AddEdge2(, , );
  406.     gh1.AddEdge2(, , );
  407.  
  408.     gh1.Display();
  409.  
  410.     gh1.BSP();
  411.     gh1.DSP();
  412.     GraphList<int, int> gMin(vArr1, sizeof(vArr1) / sizeof(vArr1[]));
  413.     GraphList<int, int> gMin1(vArr1, sizeof(vArr1) / sizeof(vArr1[]));
  414.     if (gh1.Kruskal(gMin))
  415.     {
  416.         cout << "kruskal最小生成树：" << endl;
  417.         gMin.Display();
  418.     }
  419.     if (gh1.Prim(gMin1))
  420.     {
  421.         cout << "prim最小生成树：" << endl;
  422.         gMin1.Display();
  423.     }
  424.  
  425.     int ret = ;
  426.     if (gh1.Dijkstra(, , ret))
  427.     {
  428.         cout <<"gh1.Dijkstra(0, 1, ret)"<< ret << endl;
  429.     }
  430.     if (gh1.Dijkstra(, , ret))
  431.     {
  432.         cout << "gh1.Dijkstra(0, 2, ret)" << ret << endl;
  433.     }
  434.     if (gh1.Dijkstra(, , ret))
  435.     {
  436.         cout << "gh1.Dijkstra(0, 3, ret)" << ret << endl;
  437.     }
  438.     if (gh1.Dijkstra(, , ret))
  439.     {
  440.         cout << "gh1.Dijkstra(0, 4, ret)" << ret << endl;
  441.     }
  442.     if (gh1.Dijkstra(, , ret))
  443.     {
  444.         cout << "gh1.Dijkstra(0, 5, ret)" << ret << endl;
  445.     }
  446.     //char vArr2[] = { 'A','B','C','D','E','F' };
  447.     //GraphList<char, int> gh(vArr2, sizeof(vArr2) / sizeof(vArr2[0]));
  448.     //gh.AddEdge2('A', 'B', 11);
  449.     //gh.AddEdge2('B', 'C', 33);
  450.     //gh.AddEdge2('C', 'D', 44);
  451.     //gh.AddEdge2('D', 'E', 55);
  452.     //gh.AddEdge2('E','F', 66);
  453.     //gh.Display();
  454.  
  455.  //   gh.BSP('A');
  456. }

参考:http://www.cnblogs.com/hxsyl/archive/2013/08/20/3270401.html

最短路径求解(Dijkstra)的更多相关文章

  1. 最短路径算法——Dijkstra,Bellman-Ford,Floyd-Warshall,Johnson

    根据DSqiu的blog整理出来 :http://dsqiu.iteye.com/blog/1689163 PS:模板是自己写的,如有错误欢迎指出~ 本文内容框架: §1 Dijkstra算法 §2 ...

  2. 最短路径算法-Dijkstra算法的应用之单词转换(词梯问题)(转)

    一,问题描述 在英文单词表中,有一些单词非常相似,它们可以通过只变换一个字符而得到另一个单词.比如:hive-->five:wine-->line:line-->nine:nine- ...

  3. 最短路径问题---Dijkstra算法详解

    侵删https://blog.csdn.net/qq_35644234/article/details/60870719 前言 Nobody can go back and start a new b ...

  4. 最短路径问题----Dijkstra算法的解释

    先上图: 现在要找到地点V1到其余各个地点的最短路径(图中数字的单位默认为km.).有一个原则是:永远找最小,确保无更小. 第一步:v1->v1,v1->v2,...v1->v7的距 ...

  5. 4003.基于Dijsktra算法的最短路径求解

    基于Dijsktra算法的最短路径求解 发布时间: 2018年11月26日 10:14   时间限制: 1000ms   内存限制: 128M 有趣的最短路...火候欠佳,目前还很难快速盲打出来,需继 ...

  6. 基于Dijsktra算法的最短路径求解

    基于Dijsktra算法的最短路径求解   描述 一张地图包括n个城市,假设城市间有m条路径(有向图),每条路径的长度已知.给定地图的一个起点城市和终点城市,利用Dijsktra算法求出起点到终点之间 ...

  7. 最短路径算法Dijkstra和A*

    在设计基于地图的游戏,特别是isometric斜45度视角游戏时,几乎必须要用到最短路径算法.Dijkstra算法是寻找当前最优路径(距离原点最近),如果遇到更短的路径,则修改路径(边松弛). Ast ...

  8. 单源最短路径（dijkstra算法）php实现

    做一个医学项目,当中在病例评分时会用到单源最短路径的算法.单源最短路径的dijkstra算法的思路例如以下: 如果存在一条从i到j的最短路径(Vi.....Vk,Vj),Vk是Vj前面的一顶点.那么( ...

  9. 最短路径之Dijkstra算法和Floyd-Warshall算法

    最短路径算法 最短路径算法通常用在寻找图中任意两个结点之间的最短路径或者是求全局最短路径,像是包括Dijkstra.A*.Bellman-Ford.SPFA(Bellman-Ford的改进版本).Fl ...

随机推荐

  1. 云计算之路-阿里云上：消灭“黑色n秒”第一招——不让CPU空闲

    昨天对“黑色n秒”问题的最终猜想以失败而告终,从而让我们结束了被动猜想阶段,进入了主动进攻阶段——出招. 今天出第一招——用C#写个小程序,让其在每个CPU核上运行一个线程,不让任何一个CPU核进入空 ...

  2. Navigation Nightmare---poj1984（多关系并查集）

    题目链接:http://poj.org/problem?id=1984 给定n个城市,m条边告诉你城市间的相对距离,接下来q组询问,问你在第几条边添加后两城市的距离. #include <ios ...

  3. Python开发【Django】：ModelForm操作

    ModelForm 内容回顾: Model - 数据库操作 - 验证 class A(MOdel): user = email = pwd = Form class LoginForm(Form): ...

  4. android Dialog官方demo

    1.普通的Dialog AlertDialog.Builder builder = new AlertDialog.Builder(this); builder.setMessage("今天 ...

  5. 一个C#读写Dxf的类库DXFLibrary

    https://github.com/Titifonky/DXFLibrary DXF 参考手册: http://docs.autodesk.com/ACD/2011/CHS/filesDXF/WSf ...

  6. spring boot 重定向

    /** * 测试各个html文件用. * @param model * @return */ @RequestMapping("home") public String home( ...

  7. PAT 1102 Invert a Binary Tree[比较简单]

    1102 Invert a Binary Tree(25 分) The following is from Max Howell @twitter: Google: 90% of our engine ...

  8. log4j2动态修改日志级别及拓展性使用

    一.供参考的完整日志配置 <?xml version="1.0" encoding="UTF-8"?> <!-- 配置LoggerConfig ...

  9. 安装WIN7时提示“缺少所需的CD/DVD驱动器设备驱动程序”

    同事机器重装Win7,先百度了一下不适合64bit,于是直接上32bit系统. BOIS设置DVD启动,把安装盘放在移动光驱里,开始安装. 在安装时出现下图错误:“缺少所需的CD/DVD驱动器设备驱动 ...

  10. 002-mybatis主配置文件

    <?xml version="1.0" encoding="UTF-8" ?><!DOCTYPE configuration PUBLIC & ...