滑动窗口的中位数 · Sliding Window Median

［抄题］：

给定一个包含 n 个整数的数组，和一个大小为 k 的滑动窗口,从左到右在数组中滑动这个窗口，找到数组中每个窗口内的中位数。(如果数组个数是偶数，则在该窗口排序数字后，返回第 N/2 个数字。)

对于数组 [1,2,7,8,5], 滑动大小 k = 3 的窗口时，返回 [2,7,7]

最初，窗口的数组是这样的：

[ | 1,2,7 | ,8,5] , 返回中位数 2;

接着，窗口继续向前滑动一次。

[1, | 2,7,8 | ,5], 返回中位数 7;

接着，窗口继续向前滑动一次。

[1,2, | 7,8,5 | ], 返回中位数 7;

[暴力解法]：

时间分析：

空间分析：

［思维问题］：

1. 不理解两个heap和窗口的大小关系：把窗口容量全扔进来，具体分到哪个格子另当别论
2. 体会到了treemap相对于heap的优越性：想romove哪个点是随便的。注意接口、实现都不是PQ,是treeset 而且树状的题想想里面装的是node还是数字

［一句话思路］：

窗口移动就是加一个元素、减一个元素，用俩函数实现，所以可以放在maxheap minheap中

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

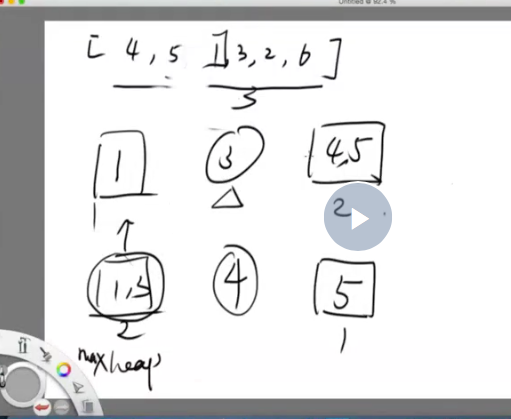
［一刷］：

1. 窗口满了之后romove第一个点，i - k + 1，不是第i个点，写习惯了就错了。重要的参数要提前注释行
2. 要在maxheap有点的前提下进行节点交换，想到其临界情况：还没有点

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

参数需要边分析边写，留意leetcode lintcode接口是不是不一样

［复杂度］：Time complexity: O(n个数*左右treeset体积lgk) Space complexity: O(n)

［英文数据结构或算法，为什么不用别的数据结构或算法］：

1. node中自己的类、自己的compareTo方法都应该有参数，否则无法调用，要理解其作用
2. 只有implements能实现接口，还是很多个。不要写extends

［关键模板化代码］：

 自制Collections.sort 方法有一个字母 第一位不相等

 自制compareTo 方法有两个字母 第二位相等

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

class Node implements Comparable<Node>{
    int id;
    int val;
    Node (int id, int val){
        this.id = id;
        this.val = val;
    }
    public int compareTo(Node other) {
        Node a = other;
        if (this.val == a.val) {
            return this.id - a.id;
        }else {
            return this.val - a.val;
        }
    }
}
 
public class Solution {
    /*
     * @param nums: A list of integers
     * @param k: An integer
     * @return: The median of the element inside the window at each moving
     */
    public double[] medianSlidingWindow(int[] nums, int k) {
        //corner case
        int n = nums.length;
        double[] result = new double[n];
        if (nums == null || k == 0) {
            return result;
        }
        TreeSet<Node> minHeap = new TreeSet<>();
        TreeSet<Node> maxHeap = new TreeSet<>();
        //add all nums into window, rest
        int half = (k + 1) / 2;
        int index = 0;
        for (int i = 0; i < k - 1; i++) {
            add(minHeap, maxHeap, half, new Node(i, nums[i]));
        }
        for (int i = k - 1; i < n; i++) {
            add(minHeap, maxHeap, half, new Node(i, nums[i]));
            nums[index] = minHeap.last().val;
            index++;
            remove(minHeap, maxHeap, new Node(i - k + 1, nums[i - k + 1]));
        }
 
        return result;
    }
 
    // write reference first!
    void add(TreeSet<Node> minHeap, TreeSet<Node> maxHeap, int size, Node node) {
        if (minHeap.size() < size) {
            minHeap.add(node);
        }else {
            maxHeap.add(node);
        }
 
        if (minHeap.size() == size) {
            //don't forget just minheap, need to ensure
            if (maxHeap.size() > 0 && minHeap.last().val > maxHeap.first().val) {
                Node b = minHeap.last();
                Node s = maxHeap.first();
                minHeap.remove(b);
                minHeap.add(s);
                maxHeap.remove(s);
                maxHeap.add(b);
            }
        }
    }
 
    void remove(TreeSet<Node> minHeap, TreeSet<Node> maxHeap, Node node) {
        if (minHeap.contains(node)) {
            minHeap.remove(node);
        }else {
            maxHeap.remove(node);
        }
    }
}

[代码风格] ：

1. 打草稿的时候先把函数参数写了 是分析出来的，不要主函数调用的时候就瞎写
2. Node 注意开头得大写