[ CQOI 2014 ] 数三角形

\(\\\)

Description

---

求 \(N\times M\) 的网格图上有多少个格点构成的三角形。

当三点共线的时候我们不认为这是一个三角形。

• \(n,m\le 10^4\)

\(\\\)

Solution

---

正难则反。容斥出答案。

总的选择三个点的方案数为 \(C_{n\times m}^3\) 。

需要去掉：

• 同一行的三个点 \(n\times C_m^3\)

• 同一列的三个点 \(m\times C_n^3\)

• 共斜线上的三个点。

但是注意！斜线的斜率可能不为 \(1\) 或 \(-1\) 。

因为有这样的东西存在：

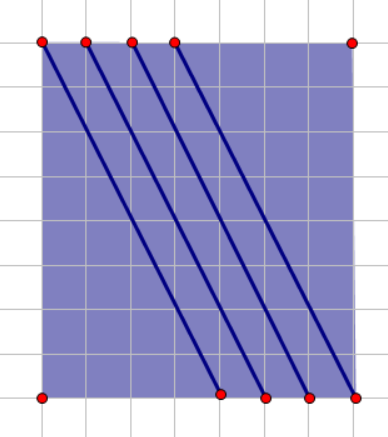
考虑怎么去掉每一条斜线上选三个整点的方案数。

这个思路就很厉害了。

考虑枚举一个向量。

对于枚举的一个向量 \((i,j)\ |\ i\le n,j\le m\) ，在整个网格图中有\((n-i)\times(m-j)\times 2\) 个线段与之对应。

解释一下 \(\times 2\) 的含义是,对斜率取相反数得到的所有线段，显然个数与原来相同。

然后为了不重复，我们强制选择线段的两个端点，然后选择一个线段上的整点。

线段上不算端点的整点个数是 \((i,j)-1\) ，因为这一线段上整点坐标只能表示为 \((\frac i{(i,j)}\times k,\frac j{(i,j)}\times k)\)

然后在总方案里去掉 \(C_{(i,j)-1}^1\times (n-i)\times (m-j)\times 2\) 就可以了。

关于正确性多说一句：

考虑两个重合的向量，大的向量计数里一定不会包含小的计数，因为小的计数的每一个情况，都有两个点在大的线段上，不符合大的计数要求。

如图，蓝线上一个合法的组合用三个箭头表示，其中必然存在形如绿色的两个箭头的选择，而他们都在黑色线段上，不符合黑色计数要求。

\(\\\)

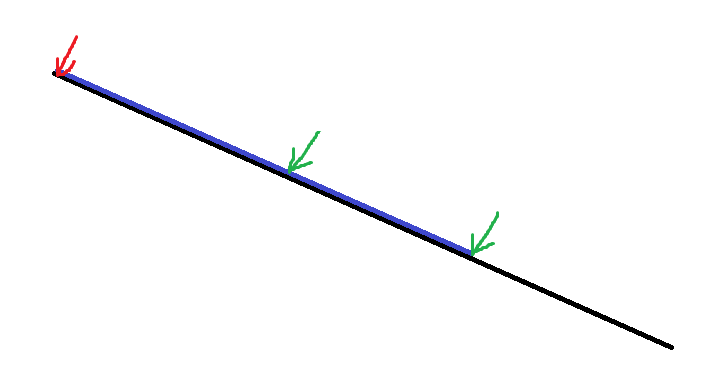
Code

---

#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define R register
using namespace std;
typedef long long ll;

ll n,m,ans;

ll C(ll x){return (x*(x-1)/2)*(x-2)/3;}

ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}

int main(){
  scanf("%lld%lld",&n,&m);
  ++n; ++m;
  ans=C(n*m)-n*C(m)-m*C(n);
  for(R ll i=1;i<=n;++i)
    for(R ll j=1,res;j<=m;++j){
      res=1+gcd(i,j);
      if(res>=3) ans-=(res-2)*(n-i)*(m-j)*2;
    }
  printf("%lld\n",ans);
  return 0;
}