C. Journey
There are n cities and n - 1 roads in the Seven Kingdoms, each road connects two cities and we can reach any city from any other by the roads.
Theon and Yara Greyjoy are on a horse in the first city, they are starting traveling through the roads. But the weather is foggy, so they can’t see where the horse brings them. When the horse reaches a city (including the first one), it goes to one of the cities connected to the current city. But it is a strange horse, it only goes to cities in which they weren't before. In each such city, the horse goes with equal probabilities and it stops when there are no such cities.
Let the length of each road be 1. The journey starts in the city 1. What is the expected length (expected value of length) of their journey? You can read about expected (average) value by the link https://en.wikipedia.org/wiki/Expected_value.
The first line contains a single integer n (1 ≤ n ≤ 100000) — number of cities.
Then n - 1 lines follow. The i-th line of these lines contains two integers ui and vi (1 ≤ ui, vi ≤ n, ui ≠ vi) — the cities connected by thei-th road.
It is guaranteed that one can reach any city from any other by the roads.
Print a number — the expected length of their journey. The journey starts in the city 1.
Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if 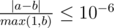 .
.
2 seconds
256 megabytes
standard input
standard output
There are n cities and n - 1 roads in the Seven Kingdoms, each road connects two cities and we can reach any city from any other by the roads.
Theon and Yara Greyjoy are on a horse in the first city, they are starting traveling through the roads. But the weather is foggy, so they can’t see where the horse brings them. When the horse reaches a city (including the first one), it goes to one of the cities connected to the current city. But it is a strange horse, it only goes to cities in which they weren't before. In each such city, the horse goes with equal probabilities and it stops when there are no such cities.
Let the length of each road be 1. The journey starts in the city 1. What is the expected length (expected value of length) of their journey? You can read about expected (average) value by the link https://en.wikipedia.org/wiki/Expected_value.
The first line contains a single integer n (1 ≤ n ≤ 100000) — number of cities.
Then n - 1 lines follow. The i-th line of these lines contains two integers ui and vi (1 ≤ ui, vi ≤ n, ui ≠ vi) — the cities connected by thei-th road.
It is guaranteed that one can reach any city from any other by the roads.
Print a number — the expected length of their journey. The journey starts in the city 1.
Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if 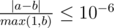 .
.
4
1 2
1 3
2 4
1.500000000000000
5
1 2
1 3
3 4
2 5
2.000000000000000
In the first sample, their journey may end in cities 3 or 4 with equal probability. The distance to city 3 is 1 and to city 4 is 2, so the expected length is 1.5.
In the second sample, their journey may end in city 4 or 5. The distance to the both cities is 2, so the expected length is 2.
题意:给你一棵树,每一条边的权值为1,让你求从1到叶子节点边权和的期望,到达每一个相邻节点的概率是一样的,不能走已走过的边。
题解:
dfs做一遍树形dp。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,m;
double ans;
struct node
{
int next,to;
}edge[];
int head[],size=;
void putin(int from,int to)
{
size++;
edge[size].to=to;
edge[size].next=head[from];
head[from]=size;
}
void dfs(int u,int fa,double s,int depth)
{
int i,cnt=;
for(i=head[u];i!=-;i=edge[i].next)if(edge[i].to!=fa)cnt++;
if(cnt==){ans+=s*(double)depth;return;}
for(i=head[u];i!=-;i=edge[i].next)
if(edge[i].to!=fa)
dfs(edge[i].to,u,s*(double)(/(double)cnt),depth+);
}
int main()
{
int i,j;
memset(head,-,sizeof(head));
scanf("%d",&n);
for(i=;i<n;i++)
{
int a,b;
scanf("%d%d",&a,&b);
putin(a,b);
putin(b,a);
}
dfs(,,,);
printf("%.15lf",ans);
return ;
}
C. Journey的更多相关文章
- CF721C. Journey[DP DAG]
C. Journey time limit per test 3 seconds memory limit per test 256 megabytes input standard input ou ...
- POJ2488A Knight's Journey[DFS]
A Knight's Journey Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 41936 Accepted: 14 ...
- CF #374 (Div. 2) C. Journey dp
1.CF #374 (Div. 2) C. Journey 2.总结:好题,这一道题,WA,MLE,TLE,RE,各种姿势都来了一遍.. 3.题意:有向无环图,找出第1个点到第n个点的一条路径 ...
- POJ2488-A Knight's Journey(DFS+回溯)
题目链接:http://poj.org/problem?id=2488 A Knight's Journey Time Limit: 1000MS Memory Limit: 65536K Tot ...
- codeforces 721C C. Journey(dp)
题目链接: C. Journey time limit per test 3 seconds memory limit per test 256 megabytes input standard in ...
- A Knight's Journey 分类: POJ 搜索 2015-08-08 07:32 2人阅读 评论(0) 收藏
A Knight's Journey Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 35564 Accepted: 12119 ...
- HDOJ-三部曲一(搜索、数学)- A Knight's Journey
A Knight's Journey Time Limit : 2000/1000ms (Java/Other) Memory Limit : 131072/65536K (Java/Other) ...
- 【推公式】UVa 10995 - Educational Journey
1A~,但后来看人家的代码好像又写臭了,T^T... Problem A: Educational journey The University of Calgary team qualified f ...
- poj 3544 Journey with Pigs
Journey with Pigs Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 3004 Accepted: 922 ...
- HDU 5477 A Sweet Journey 水题
A Sweet Journey Time Limit: 1 Sec Memory Limit: 256 MB 题目连接 http://acm.hdu.edu.cn/showproblem.php?pi ...
随机推荐
- springMVC源代码阅读之servlet部分<一>servlet部分详解
[一]servlet的概念
- 变废为宝,用旧电脑自己DIY组建 NAS 服务器
i17986 出品,必属佳作! 前言: 老外不喜欢升级硬件和软件,大家应该都知道.我昨天无意看到 FreeNAS 自述文件,这个系统可以让你使用旧的计算机硬件,于是我决定这么做.垃圾电脑你怎么能没有, ...
- 洛谷 P4512 [模板] 多项式除法
题目:https://www.luogu.org/problemnew/show/P4512 看博客:https://www.cnblogs.com/owenyu/p/6724611.html htt ...
- 实际用户ID和有效用户ID (三) *****
我们知道权限有r,w,x.其实除了这三个,还有特殊权限.比如: [root@localhost ~]# ls -l /usr/bin/passwd -rwsr-xr-x 1 root root 229 ...
- source和sh执行脚本时的差异
在CentOS7下,有如下脚:sh02.sh. 1 用sh或者bash执行 先执行echo $firstname $lastname 再执行 sh sh02.sh 最后执行 echo $firstna ...
- jsonp实现数据跨域请求
1.我们知道,哪怕跨域js文件中的代码(当然指符合web脚本安全策略的),web页面也是可以无条件执行的. 远程服务器remoteserver.com根目录下有个remote.js文件代码如下: al ...
- RequestsLibrary库入门介绍
Robot framework也可以进行接口测试,只需要导入相应的RequestsLibrary库即可. 一.准备工作: 首先需要安装好Robot framework基础环境,前面已做说明,本文就不做 ...
- You have configured this virtual machine to use a 64-bit guest operating system. However, 64-bit
vm虚拟机 问题:You have configured this virtual machine to use a 64-bit guest operating system. However, ...
- SetCapture到底是什么?
函数功能:该函数在属于当前线程的指定窗口里设置鼠标捕获.一旦窗口捕获了鼠标,所有鼠标输入都针对该窗口,无论光标是否在窗口的边界内.同一时刻只能有一个窗口捕获鼠标.如果鼠标光标在另一个线程创建的窗口上, ...
- rest framework 认证
一.简单认证示例 需求: 用户名密码正确:没有 token 则产生一个 token,有 token 则更新,返回登录成功: 若用户名或密码错误,返回错误信息. 1.models.py from dja ...
