LeetCode：访问所有节点的最短路径【847】

题目描述

给出 graph 为有 N 个节点（编号为 0, 1, 2, ..., N-1）的无向连通图。

graph.length = N，且只有节点 i 和 j 连通时，j != i 在列表 graph[i] 中恰好出现一次。

返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止，也可以多次重访节点，并且可以重用边。

示例 1：

输入：[[1,2,3],[0],[0],[0]]

输出：4

解释：一个可能的路径为 [1,0,2,0,3]

示例 2：

输入：[[1],[0,2,4],[1,3,4],[2],[1,2]]

输出：4

解释：一个可能的路径为 [0,1,4,2,3]

提示：

1 <= graph.length <= 12
0 <= graph[i].length < graph.length

题目分析

　　1.拿到这个问题时，我们先进行初步分析：

　　　　分析示例，我们可以知道每个节点是可以被重复访问的，这样子就出现了一个问题，很有可能程序将陷入一个死循环，不断在某几个节点直接无线循环下去。

　　　　为了解决这个问题，我们可以使用二进制值来保存节点的访问状态：

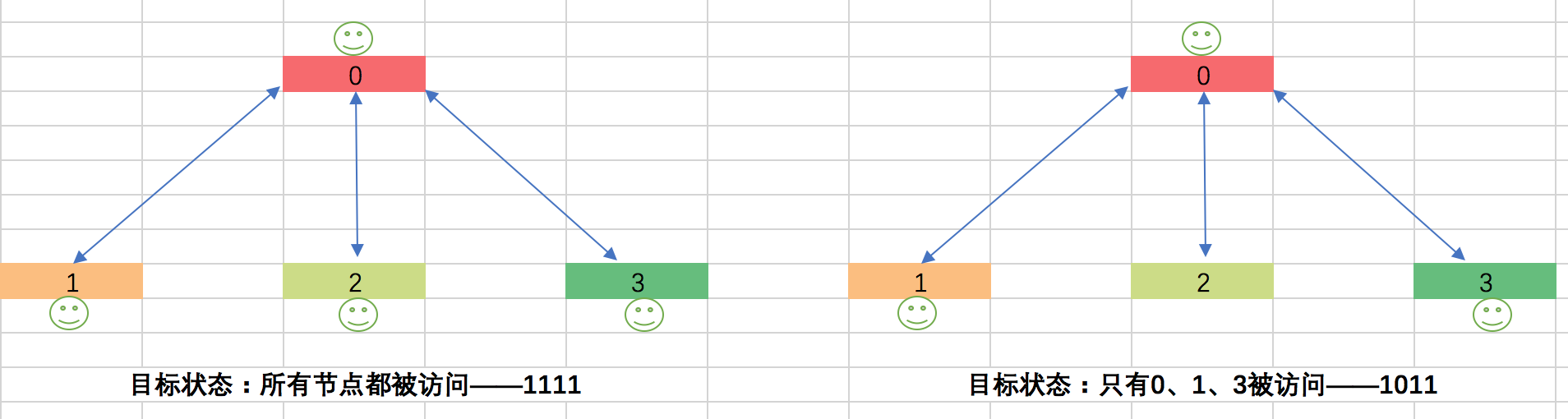
　　2.该用什么算法来描述访问所有节点的问题呢？

　　　　访问所有节点其实就是一种搜索算法，只是现在我们不是搜索每个确定的节点值，而是有条件的状态搜索（比如目标状态为1111）。

　　　　题目中说，你可以在任一节点开始和停止，那每个节点都应该是搜索的一种初始状态，并且从每个节点的这个初始状态去探索其他状态，并且最终找到目标状态前，遍历了所有的可能性，是一种典型的BFS算法应用。

　　3.BFS算法的过程是怎么样的？

　　　　我们都知道BFS搜索的算法描述是一棵树，那么算法的第一层是每个节点，接下来每层数的扩展都算路径中的一步（因为每一层代表了所有的可能性，在这么多可能性中至少有一种是可以最终找到目标状态的），最后知道找到目标状态，返回的步骤就是最短路径。

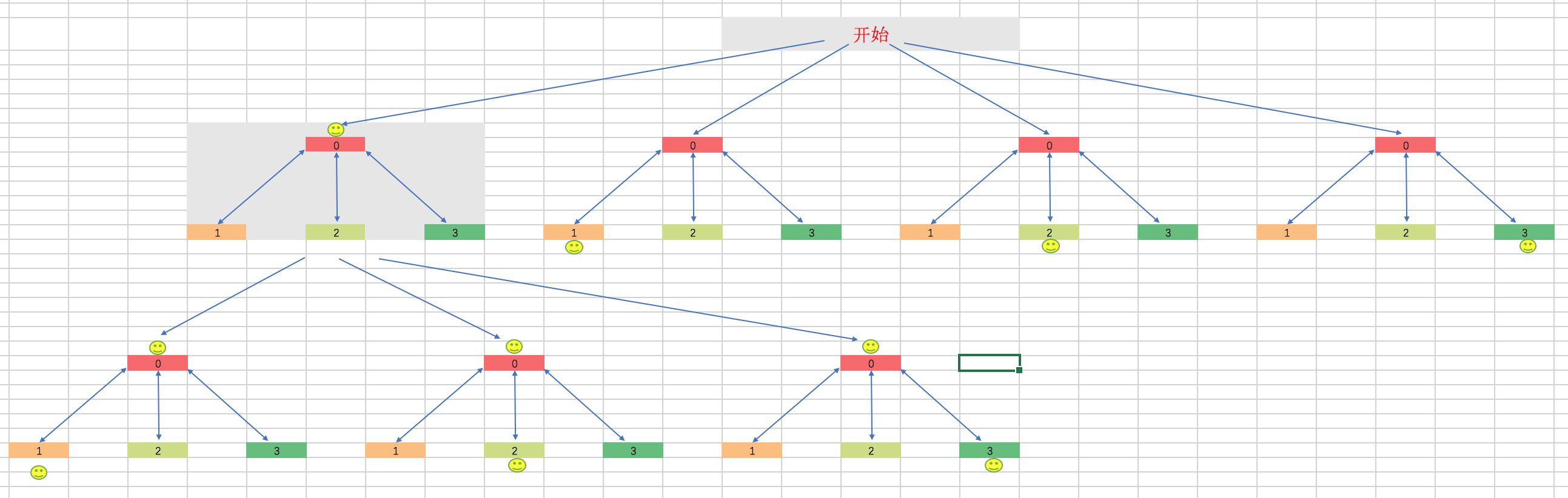
　　4.二进制状态与搜索的互相作用是怎么样的？

　　　　我们说了每一次搜索都要参考二进制状态，来避免死循环。每个节点都要一张所有状态的表格，比如第一个节点的某个状态被激活了，后来在某一次搜索中又回到第一个节点，并且状态发现这个状态出现过，那么很显然，这样走下去就会死循环，我们就可以跳过这种情况。

　　　　这样会出现一个情况，同一种状态，对于不同节点来说是不一样的，对于1号节点可能是死循环，但是对与2号节点来说很可能是正常的。

　　5.节点与状态之间的转换是怎样的？就是从一个节点到另一个节点，状态是怎么变化的？

　　　　这里我们采用了或的方式来进行状态转换控制，比如访问0号节点的时候状态是0001，接下来要访问2号节点，那么状态就会变为（0001 | 0100 =0101）！

Java实现

package graph;

import java.util.LinkedList;

import java.util.Queue;

public class ShortestPathLength_847 {

    public int shortestPathLength(int[][] graph) {

        int kAns = (1<<graph.length)-1;

        Queue<Pair>  q  = new LinkedList<>();

        int[][] visited = new int[graph.length][1<<graph.length];

        for(int i=0;i<graph.length;i++)

            q.offer(new Pair(i,1<<i));

        int steps =0;

        while (!q.isEmpty())

        {

            int s = q.size();

            while (s-->0)

            {

                Pair pair = q.poll();

                int n = pair.i;

                int state = pair.j;

                if(state==kAns)

                    return steps;

                if(visited[n][state]==1)

                    continue;

                visited[n][state]=1;

                for(int next:graph[n])

                    q.offer(new Pair(next,state|(1<<next)));

            }

            steps++;

        }

        return -1;

    }

class Pair{

    int i,j;

    public Pair(int i, int j) {

        this.i = i;

        this.j = j;

    }

}