ACM学习历程——UVA10112 Myacm Triangles（计算几何，多边形与点的包含关系）

Description

 

Problem B: Myacm Triangles

Problem B: Myacm Triangles

Source file:	triangle.{c, cpp, java, pas}
Input file:	triangle.in
Output file:	triangle.out

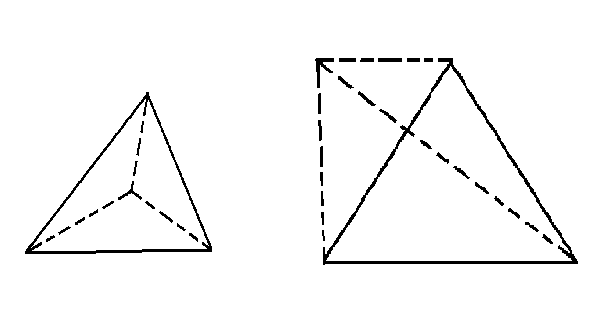
There has been considerable archeological work on the ancient Myacm culture. Many artifacts have been found in what have been called power fields: a fairly small area, less than 100 meters square where there are from four to fifteen tall monuments with crystals on top. Such an area is mapped out above. Most of the artifacts discovered have come from inside a triangular area between just three of the monuments, now called the power triangle. After considerable analysis archeologists agree how this triangle is selected from all the triangles with three monuments as vertices: it is the triangle with the largest possible area that does not contain any other monuments inside the triangle or on an edge of the triangle. Each field contains only one such triangle.

Archeological teams are continuing to find more power fields. They would like to automate the task of locating the power triangles in power fields. Write a program that takes the positions of the monuments in any number of power fields as input and determines the power triangle for each power field.

A useful formula: the area of a triangle with vertices (x₁, y₁), (x₂, y₂), and (x₃, y₃) is the absolute value of

0.5 × [(    y₃-y₁)(    x₂-x₁)     - (    y₂-y₁)(    x₃-x₁)].

For each power field there are several lines of data. The first line is the number of monuments: at least 4, and at most 15. For each monument there is a data line that starts with a one character label for the monument and is followed by the coordinates of the monument, which are nonnegative integers less than 100. The first label is A, and the next is B, and so on.

There is at least one such power field described. The end of input is indicated by a 0 for the number of monuments. The first sample data below corresponds to the diagram in the problem.

For each power field there is one line of output. It contains the three labels of the vertices of the power triangle, listed in increasing alphabetical order, with no spaces.

Example input:

6
A 1 0
B 4 0
C 0 3
D 1 3
E 4 4
F 0 6
4
A 0 0
B 1 0
C 99 0
D 99 99
0

Example output:

BEF
BCD

这个题目关键在于如何判断某个点是否在三角形中，如果解决了直接暴力枚举即可。

要判断某个点是否在三角形中，此处采用了向量积：

只要这个点与三角形三个点的连线是顺时针或逆时针依次排列，那么这个点便在三角形中，于是只要判断，相邻两个连线的数量积是否恒为正数或负数。

代码：

  1 #include <iostream>
  2 #include <cstdio>
  3 #include <cstdlib>
  4 #include <cstring>
  5 #include <cmath>
  6 #include <algorithm>
  7 #include <set>
  8 #include <map>
  9 #include <vector>
 10 #include <queue>
 11 #include <string>
 12 #define inf 0x3fffffff
 13 #define eps 1e-10
 14
 15 using namespace std;
 16
 17 struct point
 18 {
 19     int x, y;
 20
 21     double xj(point a, point b)
 22     {
 23         double ans;
 24         ans = (b.y-y) * (a.x-x) - (a.y-y) * (b.x-x);
 25         return ans;
 26     }
 27
 28     double area(point a, point b)
 29     {
 30         return fabs(xj(a, b)) / 2;
 31     }
 32
 33     bool in(point a, point b, point c)
 34     {
 35         double i, j, k;
 36         i = xj(a, b);
 37         j = xj(b, c);
 38         k = xj(c, a);
 39         if (i <= 0 &&
 40             j <= 0 &&
 41             k <= 0)
 42             return 1;
 43         if (i >= 0 &&
 44             j >= 0 &&
 45             k >= 0)
 46             return 1;
 47         return 0;
 48     }
 49 };
 50
 51 point v[16];
 52 int n;
 53 int ans[3];
 54
 55 void Input()
 56 {
 57     char ch[3];
 58     for (int i = 0; i < n; ++i)
 59         scanf("%s%d%d", ch, &v[i].x, &v[i].y);
 60 }
 61
 62 void Output()
 63 {
 64     sort(ans, ans+3);
 65     for (int i = 0; i < 3; ++i)
 66         printf("%c", ans[i]+'A');
 67     printf("\n");
 68 }
 69
 70 void qt()
 71 {
 72     double Max, t;
 73     bool flag = 1, ok;
 74     for (int i = 0; i < n; ++i)
 75         for (int j = i+1; j < n; ++j)
 76             for (int k = j+1; k < n; ++k)
 77             {
 78                 ok = 1;
 79                 for (int x = 0; x < n; ++x)
 80                 {
 81                     if (x == i ||
 82                         x == j ||
 83                         x == k)
 84                         continue;
 85                     if (v[x].in(v[i], v[j], v[k]))
 86                     {
 87                         ok = 0;
 88                         break;
 89                     }
 90                 }
 91                 if (!ok)
 92                     continue;
 93                 t = v[i].area(v[j], v[k]);
 94                 if (flag)
 95                 {
 96                     Max = t;
 97                     ans[0] = i;
 98                     ans[1] = j;
 99                     ans[2] = k;
100                     flag = 0;
101                 }
102                 else if (Max < t)
103                 {
104                     Max = t;
105                     ans[0] = i;
106                     ans[1] = j;
107                     ans[2] = k;
108                 }
109             }
110 }
111
112 int main()
113 {
114     //freopen("test.txt", "r", stdin);
115     while (scanf("%d", &n) != EOF && n)
116     {
117         Input();
118         qt();
119         Output();
120     }
121     return 0;
122 }