洛谷 P2403 [SDOI2010]所驼门王的宝藏 题解

题目描述

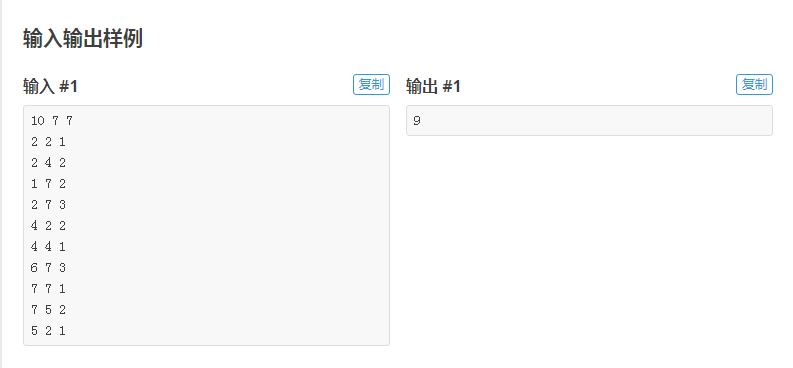
分析

先放一张图便于理解



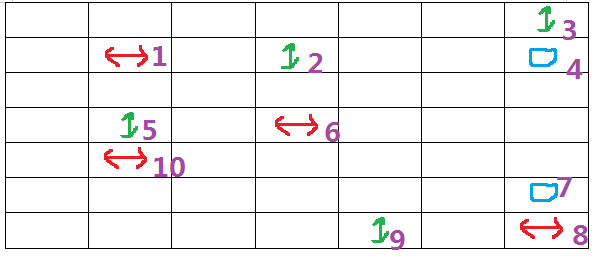
这一道题如果暴力建图会被卡成\(n^{2}\)

实际上，在我们暴力建图的时候，有很多边都是重复的

假如一行当中有许多横天门的话，我们就不必要把这一行当中的所有点和每一个横天门都连上一条边

因为横天门之间是相互联通的，无论我们走到哪一个横天门，都可以走到同一行的另一个横天门

因此，我们可以先把这些横天门连成一个环，在这些横天门中选取一个点作为代表，连向同一行中不是横天门的点

对于纵寰门也是如此

剩下的任意门直接暴力扫一遍建边即可

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e6+5;
int head[maxn],tot=1;
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0' || ch>'9'){
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0' && ch<='9'){
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    return x*f;
}
int dx[10]={0,0,1,-1,1,1,-1,-1};
int dy[10]={1,-1,0,0,-1,1,-1,1};
struct asd{
    int to,next;
}b[maxn];
void ad(int aa,int bb){
    b[tot].to=bb;
    b[tot].next=head[aa];
    head[aa]=tot++;
}
struct jll{
    int jlx,jly,jlb,id;
}jl[maxn];
int n,r,c,nx,ny,nb,rd[maxn];
int dfn[maxn],low[maxn],dfnc,sta[maxn],top,js,shuyu[maxn],siz[maxn];
void tar(int xx){
    dfn[xx]=low[xx]=++dfnc;
    sta[++top]=xx;
    for(int i=head[xx];i!=-1;i=b[i].next){
        int u=b[i].to;
        if(!dfn[u]){
            tar(u);
            low[xx]=min(low[u],low[xx]);
        } else if(!shuyu[u]){
            low[xx]=min(low[xx],dfn[u]);
        }
    }
    if(dfn[xx]==low[xx]){
        js++;
        while(1){
            int now=sta[top--];
            shuyu[now]=js;
            siz[js]++;
            if(now==xx) break;
        }
    }
}
map<pair<int,int>,bool> mp;
struct asd2{
    int to,next,val;
}b2[maxn];
int h2[maxn],t2=1;
void ad2(int aa,int bb,int cc){
    b2[t2].to=bb;
    b2[t2].next=h2[aa];
    b2[t2].val=cc;
    h2[aa]=t2++;
}
int f[maxn],ans=0;
void tp(){
    queue<int> q;
    q.push(0);
    while(!q.empty()){
        int now=q.front();
        q.pop();
        for(int i=h2[now];i!=-1;i=b2[i].next){
            int u=b2[i].to;
            rd[u]--;
            f[u]=max(f[u],f[now]+b2[i].val);
            if(rd[u]==0) q.push(u);
        }
    }
}
bool cmplh(jll aa,jll bb){
    if(aa.jlb==bb.jlb && aa.jlx==bb.jlx) return aa.jly<bb.jly;
    if(aa.jlb==bb.jlb) return aa.jlx<bb.jlx;
    return aa.jlb<bb.jlb;
}
bool cmpll(jll aa,jll bb){
    if(aa.jlb==bb.jlb && aa.jly==bb.jly) return aa.jlx<bb.jlx;
    if(aa.jlb==bb.jlb) return aa.jly<bb.jly;
    if(aa.jlb==2) return 1;
    return 0;
}
bool cmpry(jll aa,jll bb){
    return aa.jlb>bb.jlb;
}
map<pair<int,int>,int> mpp;
int htm[maxn],ztm[maxn];
int main(){
    memset(head,-1,sizeof(head));
    memset(h2,-1,sizeof(h2));
    n=read(),r=read(),c=read();
    for(int i=1;i<=n;i++){
        jl[i].jlx=read();
        jl[i].jly=read();
        jl[i].jlb=read();
        jl[i].id=i;
        mpp[make_pair(jl[i].jlx,jl[i].jly)]=jl[i].id;
    }
    sort(jl+1,jl+1+n,cmplh);
    for(int i=1;i<=n;i++){
        if(jl[i].jlb!=1) break;
        int ks=jl[i].id;
        while(jl[i].jlx==jl[i+1].jlx && jl[i+1].jlb==1){
            ad(jl[i].id,jl[i+1].id);
            i++;
        }
        ad(jl[i].id,ks);
        htm[jl[i].jlx]=jl[i].id;
    }
    sort(jl+1,jl+1+n,cmpll);
    for(int i=1;i<=n;i++){
        if(jl[i].jlb!=2) break;
        int ks=jl[i].id;
        while(jl[i].jly==jl[i+1].jly && jl[i+1].jlb==2){
            ad(jl[i].id,jl[i+1].id);
            i++;
        }
        ad(jl[i].id,ks);
        ztm[jl[i].jly]=jl[i].id;
    }
    sort(jl+1,jl+1+n,cmpry);
    for(int i=1;i<=n;i++){
        if(jl[i].jlb!=3) break;
        int nx=jl[i].jlx,ny=jl[i].jly;
        for(int j=0;j<8;j++){
            int mx=nx+dx[j];
            int my=ny+dy[j];
            if(mpp[make_pair(mx,my)]){
                ad(jl[i].id,mpp[make_pair(mx,my)]);
            }
        }
    }
    for(int i=1;i<=n;i++){
        if(jl[i].jlb==1) continue;
        int ks=jl[i].id;
        if(htm[jl[i].jlx]!=0) ad(htm[jl[i].jlx],jl[i].id);
    }
    for(int i=1;i<=n;i++){
        if(jl[i].jlb==2) continue;
        int ks=jl[i].id;
        if(ztm[jl[i].jly]!=0) ad(ztm[jl[i].jly],jl[i].id);
    }
    for(int i=1;i<=n;i++){
        if(!dfn[i]) tar(i);
    }
    for(int i=1;i<=n;i++){
        for(int j=head[i];j!=-1;j=b[j].next){
            int u=b[j].to;
            if(shuyu[i]!=shuyu[u] && mp[make_pair(shuyu[i],shuyu[u])]==0){
                ad2(shuyu[i],shuyu[u],siz[shuyu[u]]);
                rd[shuyu[u]]++;
                mp[make_pair(shuyu[i],shuyu[u])]=1;
            }
        }
    }
    for(int i=1;i<=js;i++){
        if(rd[i]==0){
            ad2(0,i,siz[i]);
            rd[i]++;
        }
    }
    tp();
    for(int i=1;i<=js;i++){
        ans=max(ans,f[i]);
    }
    printf("%d\n",ans);
    return 0;
}