JPEG解码——(6)IDCT逆离散余弦变换

　　本篇是该系列的第六篇，承接上篇IZigZag变换，介绍接下来的一个步骤——逆离散余弦变换，即逆零偏置前的一个步骤。

　　该步骤比较偏理论，其业务是对IZigZag变换后的数据，再进一步的处理，使其恢复DCT变换前的数据。

　　需要补充一点说明的是，上面的DCT其实是DCT2，因为jpeg编码下都是对8x8的像素块进行处理。

1. 理论

　　1.1. 背景

　　　　DCT，即离散余弦变换，常用图像压缩算法，步骤如下

　　　　1）分割，首先将图像分割成8x8或16x16的小块；
　　　　2）DCT变换，对每个小块进行DCT变换；
　　　　3）舍弃高频系数（AC系数），保留低频信息（DC系数）。高频系数一般保存的是图像的边界、纹理信息，低频信息主要是保存的图像中平坦区域信息。
　　　　4）图像的低频和高频，高频区域指的是空域图像中突变程度大的区域（比如目标边界区域），通常的纹理丰富区域。

　　1.2.算法

　　　　二维DCT变换就是将二维图像从空间域转换到频率域。形象的说，就是计算出图像由哪些二维余弦波构成。其算法如下：

　　　　

　　　　其中，F就是变换得到的系数，f是图像的像素值，A是转换矩阵，其中i为二维波的水平方向频率，j为二维波的垂直方向频率，取值范围都是0-(N-1)，N是图像块的大小，其中：

　　　　

　　　　即进行如下步骤的处理可以得到DCT变换后的系数矩阵：

　　　　1）求出转换矩阵A；
　　　　2）利用转换矩阵A，转换到频域，即由图像 f 得到系数矩阵F。

2. 实践

　　2.1. 图像上运用实现

　　　　DCT用图像上的处理，都是对8x8的像素数据块进行处理，因此，DCT2变换的转换矩阵A为：

　　　　

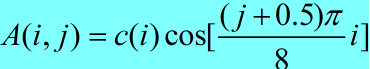
　　　　其中，

　　　　 

　　　　那么转换矩阵A为：

　　　　

　　　　计算如这个链接：

 1 void InitTransMat()
 2 {
 3     int i,j;
 4     float a;
 5
 6     for(i=0;i<MAT_SIZE;i++)
 7     {
 8         for(j=0;j<MAT_SIZE;j++)
 9         {
10             a = 0;
11             if(i==0)
12             {
13                 a=sqrt((float)1/MAT_SIZE);
14             }
15             else
16             {
17                 a=sqrt((float)2/MAT_SIZE);
18             }
19             DCT_Mat[i][j]= a*cos((j+0.5)*PI*i/MAT_SIZE); //变换矩阵
20         }
21     }
22     /* only for 8x8 */
23     //float Tmp[100][100] = {
24     //    {0.3536,    0.3536,    0.3536,    0.3536,    0.3536,    0.3536,    0.3536,    0.3536,},
25     //    {0.4904,    0.4157,    0.2778,    0.0975,   -0.0975,   -0.2778,   -0.4157,   -0.4904,},
26     //    {0.4619,    0.1913,   -0.1913,   -0.4619,   -0.4619,   -0.1913,    0.1913,    0.4619,},
27     //    {0.4157,   -0.0975,   -0.4904,   -0.2778,    0.2778,    0.4904,    0.0975,   -0.4157,},
28     //    {0.3536,   -0.3536,   -0.3536,    0.3536,    0.3536,   -0.3536,   -0.3536,    0.3536,},
29     //    {0.2778,   -0.4904,    0.0975,    0.4157,   -0.4157,   -0.0975,    0.4904,   -0.2778,},
30     //    {0.1913,   -0.4619,    0.4619,   -0.1913,   -0.1913,    0.4619,   -0.4619,    0.1913,},
31     //    {0.0975,   -0.2778,    0.4157,   -0.4904,    0.4904,   -0.4157,    0.2778,   -0.0975,},
32     //};
33     //for (int i=0; i<8; i++)
34     //    for (int j=0; j<8; j++)
35     //        DCT_Mat[i][j] = Tmp[i][j];
36 }

　　2.2. IDCT2—— 由F求f的过程

　　　　前篇文章已介绍了由IZigZag变换后得到的系数矩阵F，那么要恢复原数据，就要进行如下变换：

　　　　

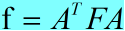
　　　　算法的C语言描述如下：

 1 int IDCT2(float (*dst)[8], int (*block)[8], bool dump)
 2 {
 3     float trans_matrix[8][8] = {
 4         {0.3536,    0.3536,    0.3536,    0.3536,    0.3536,    0.3536,    0.3536,    0.3536,},
 5         {0.4904,    0.4157,    0.2778,    0.0975,   -0.0975,   -0.2778,   -0.4157,   -0.4904,},
 6         {0.4619,    0.1913,   -0.1913,   -0.4619,   -0.4619,   -0.1913,    0.1913,    0.4619,},
 7         {0.4157,   -0.0975,   -0.4904,   -0.2778,    0.2778,    0.4904,    0.0975,   -0.4157,},
 8         {0.3536,   -0.3536,   -0.3536,    0.3536,    0.3536,   -0.3536,   -0.3536,    0.3536,},
 9         {0.2778,   -0.4904,    0.0975,    0.4157,   -0.4157,   -0.0975,    0.4904,   -0.2778,},
10         {0.1913,   -0.4619,    0.4619,   -0.1913,   -0.1913,    0.4619,   -0.4619,    0.1913,},
11         {0.0975,   -0.2778,    0.4157,   -0.4904,    0.4904,   -0.4157,    0.2778,   -0.0975,},
12     };
13
14     float tmp[8][8];
15
16     float t=0;
17     int i,j,k;
18     for(i=0;i<8;i++)  //same as A'*I
19     {
20         for(j=0;j<8;j++)
21         {
22             t = 0;
23             for(k=0; k<8; k++)
24             {
25                 t += trans_matrix[k][i] * block[k][j]; //trans_matrix's ith column * block's jth column
26             }
27             tmp[i][j] = t;
28         }
29     }
30
31     for(i=0; i<8; i++)  //same as tmp*A
32     {
33         for(j=0; j<8; j++)
34         {
35             t=0;
36             for(k=0; k<8; k++)
37             {
38                 t += tmp[i][k] * trans_matrix[k][j];
39             }
40             dst[i][j] = t;
41         }
42     }
43
44     if (dump) {
45         puts("----after idct2----");
46         for (i=0; i<8; i++) {
47             for (j=0; j<8; j++) {
48                 printf("%3.4f  ", dst[i][j]);
49             }
50             puts("");
51         }
52         puts("");
53     }
54
55     return 0;
56 }

　　2.3. 例子实践

　　　　根据前篇文章的IZigZag结果恢复数据，如下：

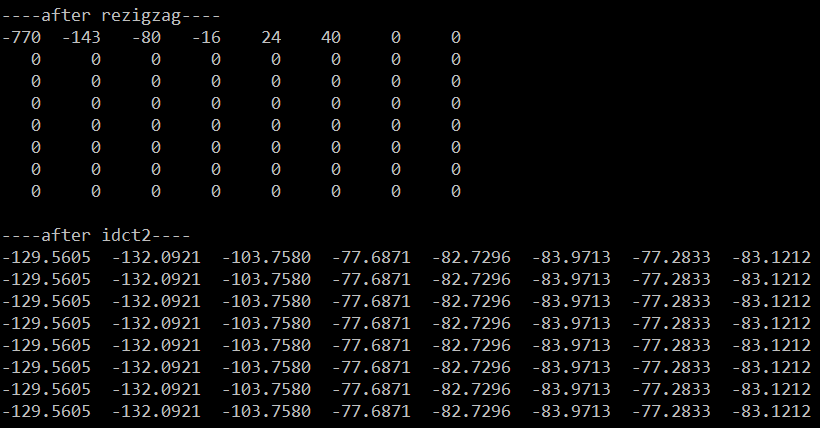
　　　　有没有注意到许多值是近似相等的？

3. 篇外补充

　　正是图像上这种特性，才有了图像压缩的这种方法——空间去冗余。

　　但是，需要说明一点的是，DCT2/IDCT2不是有损失压缩（压缩是数据量降低的概念，有损/无损是转换前后信息是否丢失的概念），因为它可以完全恢复数据，只是这种变换将图像在空间域/频率域之间转换。

　　空间域的数据量很多，但是经DCT2转换后，数据量变得非常少（非0数据），这个例子可能看的还不是太直观但有了初步雏形。

　　在这里，要特别感谢傅里叶这位法国数学家，正是因为他的出色工作，才使得如今的最常见的图像压缩技术变成了现实。

　　正可谓，前人栽树后人乘凉。前人的理论成果，后人在应用上开花结果。