通俗理解隐马尔科夫模型HMM（转载）

作者：Yang Eninala 链接：https://www.zhihu.com/question/20962240/answer/33438846 来源：知乎 著作权归作者所有，转载请联系作者获得授权。

 

 

 

隐马尔可夫（HMM）好讲，简单易懂不好讲。我认为 @者也的回答没什么错误，不过我想说个更通俗易懂的例子。我希望我的读者不是专家，而是对这个问题感兴趣的入门者，所以我会多阐述数学思想，少写公式。霍金曾经说过，你多写一个公式，就会少一半的读者。所以时间简史这本关于物理的书和麦当娜关于性的书卖的一样好。我会效仿这一做法，写最通俗易懂的答案。
还是用最经典的例子，掷骰子。假设我手里有三个不同的骰子。第一个骰子是我们平常见的骰子（称这个骰子为D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6。第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是1/4。第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8。
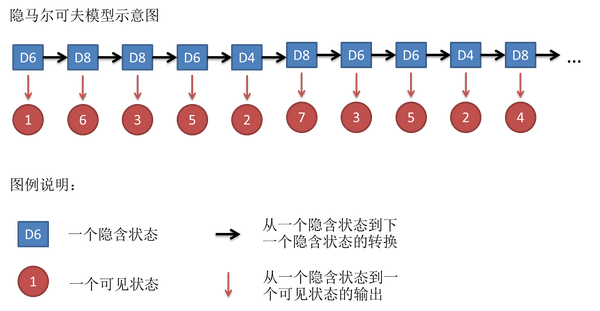
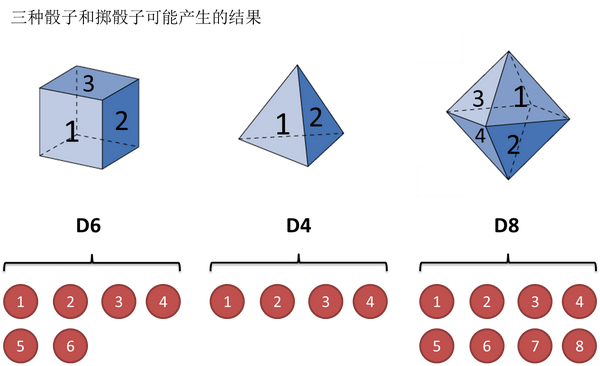假设我们开始掷骰子，我们先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。然后我们掷骰子，得到一个数字，1，2，3，4，5，6，7，8中的一个。不停的重复上述过程，我们会得到一串数字，每个数字都是1，2，3，4，5，6，7，8中的一个。例如我们可能得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4
这串数字叫做可见状态链。但是在隐马尔可夫模型中，我们不仅仅有这么一串可见状态链，还有一串隐含状态链。在这个例子里，这串隐含状态链就是你用的骰子的序列。比如，隐含状态链有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8
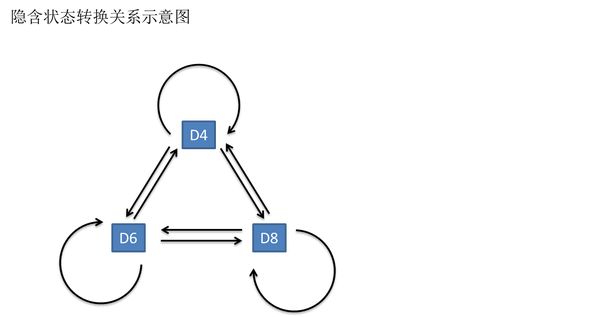
一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率（transition probability）。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。
同样的，尽管可见状态之间没有转换概率，但是隐含状态和可见状态之间有一个概率叫做输出概率（emission probability）。就我们的例子来说，六面骰（D6）产生1的输出概率是1/6。产生2，3，4，5，6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如，我有一个被赌场动过手脚的六面骰子，掷出来是1的概率更大，是1/2，掷出来是2，3，4，5，6的概率是1/10。
其实对于HMM来说，如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率，做模拟是相当容易的。但是应用HMM模型时候呢，往往是缺失了一部分信息的，有时候你知道骰子有几种，每种骰子是什么，但是不知道掷出来的骰子序列；有时候你只是看到了很多次掷骰子的结果，剩下的什么都不知道。如果应用算法去估计这些缺失的信息，就成了一个很重要的问题。这些算法我会在下面详细讲。
××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××× 如果你只想看一个简单易懂的例子，就不需要往下看了。 ××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××× 说两句废话，答主认为呢，要了解一个算法，要做到以下两点：会其意，知其形。答主回答的，其实主要是第一点。但是这一点呢，恰恰是最重要，而且很多书上不会讲的。正如你在追一个姑娘，姑娘对你说“你什么都没做错！”你要是只看姑娘的表达形式呢，认为自己什么都没做错，显然就理解错了。你要理会姑娘的意思，“你赶紧给我道歉！”这样当你看到对应的表达形式呢，赶紧认错，跪地求饶就对了。数学也是一样，你要是不理解意思，光看公式，往往一头雾水。不过呢，数学的表达顶多也就是晦涩了点，姑娘的表达呢，有的时候就完全和本意相反。所以答主一直认为理解姑娘比理解数学难多了。
回到正题，和HMM模型相关的算法主要分为三类，分别解决三种问题：
1）知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道每次掷出来的都是哪种骰子（隐含状态链）。 这个问题呢，在语音识别领域呢，叫做解码问题。这个问题其实有两种解法，会给出两个不同的答案。每个答案都对，只不过这些答案的意义不一样。第一种解法求最大似然状态路径，说通俗点呢，就是我求一串骰子序列，这串骰子序列产生观测结果的概率最大。第二种解法呢，就不是求一组骰子序列了，而是求每次掷出的骰子分别是某种骰子的概率。比如说我看到结果后，我可以求得第一次掷骰子是D4的概率是0.5，D6的概率是0.3，D8的概率是0.2.第一种解法我会在下面说到，但是第二种解法我就不写在这里了，如果大家有兴趣，我们另开一个问题继续写吧。
2）还是知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率），根据掷骰子掷出的结果（可见状态链），我想知道掷出这个结果的概率。 看似这个问题意义不大，因为你掷出来的结果很多时候都对应了一个比较大的概率。问这个问题的目的呢，其实是检测观察到的结果和已知的模型是否吻合。如果很多次结果都对应了比较小的概率，那么就说明我们已知的模型很有可能是错的，有人偷偷把我们的骰子給换了。
3）知道骰子有几种（隐含状态数量），不知道每种骰子是什么（转换概率），观测到很多次掷骰子的结果（可见状态链），我想反推出每种骰子是什么（转换概率）。 这个问题很重要，因为这是最常见的情况。很多时候我们只有可见结果，不知道HMM模型里的参数，我们需要从可见结果估计出这些参数，这是建模的一个必要步骤。
问题阐述完了，下面就开始说解法。（0号问题在上面没有提，只是作为解决上述问题的一个辅助）
0.一个简单问题 其实这个问题实用价值不高。由于对下面较难的问题有帮助，所以先在这里提一下。
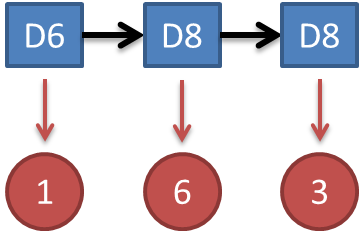
知道骰子有几种，每种骰子是什么，每次掷的都是什么骰子，根据掷骰子掷出的结果，求产生这个结果的概率。解法无非就是概率相乘：
1.看见不可见的，破解骰子序列 这里我说的是第一种解法，解最大似然路径问题。 举例来说，我知道我有三个骰子，六面骰，四面骰，八面骰。我也知道我掷了十次的结果（1 6 3 5 2 7 3 5 2 4），我不知道每次用了那种骰子，我想知道最有可能的骰子序列。
其实最简单而暴力的方法就是穷举所有可能的骰子序列，然后依照第零个问题的解法把每个序列对应的概率算出来。然后我们从里面把对应最大概率的序列挑出来就行了。如果马尔可夫链不长，当然可行。如果长的话，穷举的数量太大，就很难完成了。
另外一种很有名的算法叫做Viterbi algorithm. 要理解这个算法，我们先看几个简单的列子。
首先，如果我们只掷一次骰子： 看到结果为1.对应的最大概率骰子序列就是D4，因为D4产生1的概率是1/4，高于1/6和1/8.
把这个情况拓展，我们掷两次骰子： 结果为1，6.这时问题变得复杂起来，我们要计算三个值，分别是第二个骰子是D6，D4，D8的最大概率。显然，要取到最大概率，第一个骰子必须为D4。这时，第二个骰子取到D6的最大概率是 同样的，我们可以计算第二个骰子是D4或D8时的最大概率。我们发现，第二个骰子取到D6的概率最大。而使这个概率最大时，第一个骰子为D4。所以最大概率骰子序列就是D4 D6。
继续拓展，我们掷三次骰子： 同样，我们计算第三个骰子分别是D6，D4，D8的最大概率。我们再次发现，要取到最大概率，第二个骰子必须为D6。这时，第三个骰子取到D4的最大概率是 同上，我们可以计算第三个骰子是D6或D8时的最大概率。我们发现，第三个骰子取到D4的概率最大。而使这个概率最大时，第二个骰子为D6，第一个骰子为D4。所以最大概率骰子序列就是D4 D6 D4。
写到这里，大家应该看出点规律了。既然掷骰子一二三次可以算，掷多少次都可以以此类推。我们发现，我们要求最大概率骰子序列时要做这么几件事情。首先，不管序列多长，要从序列长度为1算起，算序列长度为1时取到每个骰子的最大概率。然后，逐渐增加长度，每增加一次长度，重新算一遍在这个长度下最后一个位置取到每个骰子的最大概率。因为上一个长度下的取到每个骰子的最大概率都算过了，重新计算的话其实不难。当我们算到最后一位时，就知道最后一位是哪个骰子的概率最大了。然后，我们要把对应这个最大概率的序列从后往前推出来。
2.谁动了我的骰子？ 比如说你怀疑自己的六面骰被赌场动过手脚了，有可能被换成另一种六面骰，这种六面骰掷出来是1的概率更大，是1/2，掷出来是2，3，4，5，6的概率是1/10。你怎么办么？答案很简单，算一算正常的三个骰子掷出一段序列的概率，再算一算不正常的六面骰和另外两个正常骰子掷出这段序列的概率。如果前者比后者小，你就要小心了。
比如说掷骰子的结果是： 要算用正常的三个骰子掷出这个结果的概率，其实就是将所有可能情况的概率进行加和计算。同样，简单而暴力的方法就是把穷举所有的骰子序列，还是计算每个骰子序列对应的概率，但是这回，我们不挑最大值了，而是把所有算出来的概率相加，得到的总概率就是我们要求的结果。这个方法依然不能应用于太长的骰子序列（马尔可夫链）。
我们会应用一个和前一个问题类似的解法，只不过前一个问题关心的是概率最大值，这个问题关心的是概率之和。解决这个问题的算法叫做前向算法（forward algorithm）。
首先，如果我们只掷一次骰子： 看到结果为1.产生这个结果的总概率可以按照如下计算，总概率为0.18： 把这个情况拓展，我们掷两次骰子： 看到结果为1，6.产生这个结果的总概率可以按照如下计算，总概率为0.05：
继续拓展，我们掷三次骰子： 看到结果为1，6，3.产生这个结果的总概率可以按照如下计算，总概率为0.03：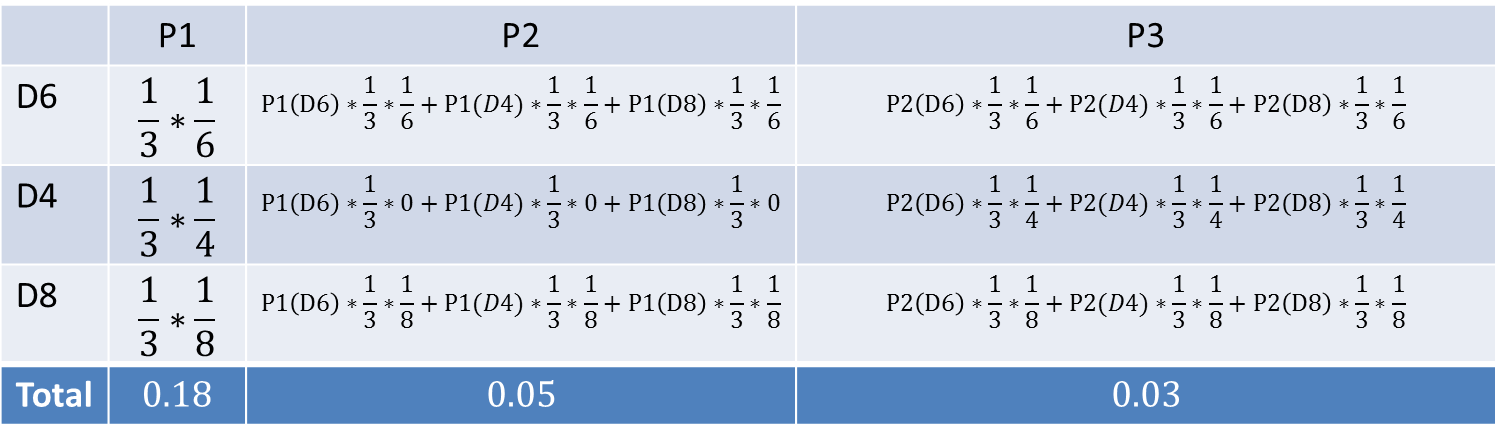
同样的，我们一步一步的算，有多长算多长，再长的马尔可夫链总能算出来的。用同样的方法，也可以算出不正常的六面骰和另外两个正常骰子掷出这段序列的概率，然后我们比较一下这两个概率大小，就能知道你的骰子是不是被人换了。
3.掷一串骰子出来，让我猜猜你是谁 （答主很懒，还没写，会写一下EM这个号称算法的方法） 上述算法呢，其实用到了递归，逆向推导，循环这些方法，我只不过用很直白的语言写出来了。如果你们去看专业书籍呢，会发现更加严谨和专业的描述。毕竟，我只做了会其意，要知其形，还是要看书的。