HDU 1828 Picture（线段树扫描线求周长）

Picture

Time Limit: 6000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4475    Accepted Submission(s): 2207

Problem Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

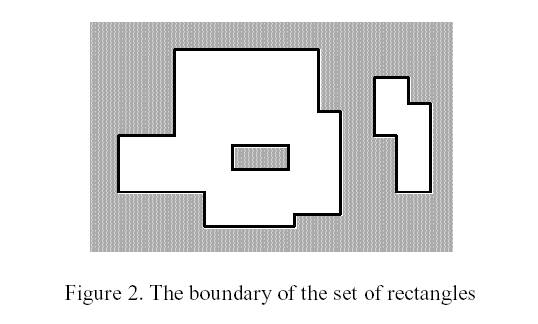
The vertices of all rectangles have integer coordinates.

 

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.

0 <= number of rectangles < 5000 
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Please process to the end of file.

 

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

 

Sample Input

7

-15 0 5 10

-5 8 20 25

15 -4 24 14

0 -6 16 4

2 15 10 22

30 10 36 20

34 0 40 16

 

Sample Output

228

题目链接：HDU 1828

扫描线第三道题目，都是整数点且范围较小不需要离散化，主要学习了如何求轮廓线的周长（内周长+外周长），有两种方法这里用的是比较好写但是速度慢的一种——横着竖着各做一次扫描线，统计横竖的周长再求和输出，过程和求面积并类似，但是每一次累加的是覆盖长度的改变量即$abs（这一次更新之后的长度-上一次的长度）$，另外要注意一点就是当高度相同时要优先更新底边。

比如这样一组数据：

2

0 0 1 1

0 1 1 2

若不这样做会得到错误答案8，但其实边长只有4+2=6，原因就是错误地把中间的边也当作影响更新长度的情况了，实际是重叠之后两条边会一起抵消掉，刚开始写完debug半天最后发现是建树时没考虑范围要可能是负数……

代码：

#include <stdio.h>
#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define CLR(arr,val) memset(arr,val,sizeof(arr))
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
typedef pair<int,int> pii;
typedef long long LL;
const double PI=acos(-1.0);
const int N=2e4+7;
struct seg
{
    int l,mid,r;
    int len,cnt;
};
struct Line
{
    int l,r,h,flag;
    inline bool operator<(const Line &t)const
    {
        if(h==t.h)//若高度相等，则底边优先
            return flag>t.flag;
        return h<t.h;
    }
};
seg T[N<<2];
Line xline[N],yline[N];

inline void pushup(int k)
{
    if(T[k].cnt)
        T[k].len=T[k].r-T[k].l+1;
    else
    {
        if(T[k].l==T[k].r)
            T[k].len=0;
        else
            T[k].len=T[LC(k)].len+T[RC(k)].len;
    }
}
void build(int k,int l,int r)
{
    T[k].l=l;
    T[k].r=r;
    T[k].mid=MID(l,r);
    T[k].cnt=0;
    T[k].len=0;
    if(l==r)
        return ;
    build(LC(k),l,T[k].mid);
    build(RC(k),T[k].mid+1,r);
}
void update(int k,int l,int r,int flag)
{
    if(l<=T[k].l&&T[k].r<=r)
    {
        T[k].cnt+=flag;
        pushup(k);
    }
    else
    {
        if(r<=T[k].mid)
            update(LC(k),l,r,flag);
        else if(l>T[k].mid)
            update(RC(k),l,r,flag);
        else
            update(LC(k),l,T[k].mid,flag),update(RC(k),T[k].mid+1,r,flag);
        pushup(k);
    }
}
int main(void)
{
    int n,i;
    int xa,xb,ya,yb;
    int ans,last;
    while (~scanf("%d",&n))
    {
        int cnt=0;
        int xR=-INF;
        int yR=-INF;
        int xL=INF;
        int yL=INF;
        for (i=0; i<n; ++i)
        {
            scanf("%d%d%d%d",&xa,&ya,&xb,&yb);
            xline[cnt]=(Line){xa,xb,ya,1};
            yline[cnt++]=(Line){ya,yb,xa,1};//
            xline[cnt]=(Line){xa,xb,yb,-1};
            yline[cnt++]=(Line){ya,yb,xb,-1};//
            if(xa>xR) xR=xa;
            if(xa<xL) xL=xa;
            if(xb>xR) xR=xb;
            if(xb<xL) xL=xb;

            if(ya>yR) yR=ya;
            if(ya<yL) yL=ya;
            if(yb>yR) yR=yb;
            if(yb<yL) yL=yb;
        }
        ans=0;
        sort(xline,xline+cnt);
        sort(yline,yline+cnt);

        last=0;
        build(1,xL,xR);
        for (i=0; i<cnt; ++i)
        {
            update(1,xline[i].l,xline[i].r-1,xline[i].flag);
            ans=ans+abs(T[1].len-last);
            last=T[1].len;
        }

        last=0;
        build(1,yL,yR);
        for (i=0; i<cnt; ++i)
        {
            update(1,yline[i].l,yline[i].r-1,yline[i].flag);
            ans=ans+abs(T[1].len-last);
            last=T[1].len;
        }

        printf("%d\n",ans);
    }
    return 0;
}