NLP复习之N元文法

N元文法的统计

二元概率方程：

\[P(w_n|w_{n-1}) = \frac{C(w_{n-1}w_n)}{C(w_{n-1})}
\]

三元概率估计方程：

\[P(w_n|w_{n-2},w_{n-1}) = \frac{C(w_{n-2;n-1}w_n)}{C(w_{n-2;n-1})}
\]

例题1

给出以下一个小型语料库，在最大似然一元模型和二元模型之间使用加一平滑法进行平滑, 请计算P(Sam|am)。注意要将tokens 和与其他单词一样看待。

<s> I am Sam </s>

<s> Sam I am </s>

<s> I am Sam </s>

<s> I do not like green eggs and Sam </s>

解

\(P(Sam|am) = \frac{C(am;Sam)}{C(am)} = \frac{2}{3}\)

\(P_{Laplace}(Sam|am) = \frac{C(am;Sam)+1}{C(am)+|V|} = \frac{2+1}{3+11} = \frac{3}{14}\)

注意：V是不同单词的种类！！是词汇表的大小

例题2

在1的条件下，请使用线性插值法，其中假设 λ1 = 1/2， λ2 =1/2，请计算P(Sam|am)。注意要将tokens 和与其他单词一样看待。

解

\(P(Sam) = \frac{C(Sam)}{S} =\frac{4}{25}\)

注意：S是单词出现的总次数！！

\(P(am) = \frac{3}{25}\)

统计\(bigram\)数量，\(P(Sam|am) = \frac{2}{3}\)

根据线性插值法，

\[\begin{aligned}
P(Sam|am) &= \lambda_2 \times P(Sam|am) + \lambda_1 \times P(Sam)\\
&= 0.5 \times \frac{2}{3} + 0.5 \times \frac{3}{25} \\
&= \frac{31}{75}
\end{aligned}
\]

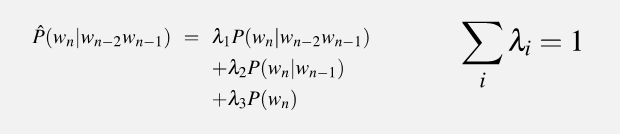
例题3

给定一个包含 100 个数字的训练集，其中包含 91 个0和 1-9 其他数字中的每个数字。 有以下的测试集：0 0 0 0 0 3 0 0 0 0。计算该问题的一元困惑度 unigram perplexity。

困惑度

\[PP(W) = P(w_1w_2 \dots w_N)^{-\frac{1}{N}}
\]

困惑度越小，概率越大。

解

\(P(0) = 91 / 100 = 0.91;\)

\(P(1;9) = 1 / 100 = 0.01;\)

\(PP(W) = (P(0)p(0)p(0)p(0)p(0)p(3)p(0)p(0)p(0)p(0))^{-0.1} = 1.725\)