NCTF2022-Crypto WP

superecc

题目

from Crypto.Util.number import *
from secrets import INF, flag

assert flag[:5] == b'nctf{'

class super_ecc:
    def __init__(self):
        self.a = 73101304688827564515346974949973801514688319206271902046500036921488731301311
        self.c = 78293161515104296317366169782119919020288033620228629011270781387408756505563
        self.d = 37207943854782934242920295594440274620695938273948375125575487686242348905415
        self.p = 101194790049284589034264952247851014979689350430642214419992564316981817280629

    def add(self, P, Q):
        (x1, y1) = P
        (x2, y2) = Q
        x3 = (x1 * y2 + y1 * x2) * inverse(self.c * (1 + self.d * x1 * x2 * y1 * y2), self.p) % self.p
        y3 = (y1 * y2 - self.a * x1 * x2) * inverse(self.c * (1 - self.d * x1 * x2 * y1 * y2), self.p) % self.p
        return (x3, y3)

    def mul(self, x, P):
        Q = INF
        x = x % self.p
        while x > 0:
            if x % 2 == 1:
                Q = self.add(Q, P)
            P = self.add(P, P)
            x = x >> 1
        return Q

flag = bytes_to_long(flag[5:-1])
ecc = super_ecc()
G = (30539694658216287049186009602647603628954716157157860526895528661673536165645,
     64972626416868540980868991814580825204126662282378873382506584276702563849986)
S = ecc.mul(flag, G)
print(S)
# (98194560294138607903211673286210561363390596541458961277934545796708736630623,
# 58504021112693314176230785309962217759011765879155504422231569879170659690008)

本题主要考察对于扭曲爱德华曲线方程到 Weierstrass 曲线的转换。

首先我们知道，本题使用的曲线方程为

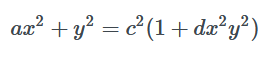
这是一个一般性的扭曲爱德华曲线方程，我们对其变形，让其成为我们熟知的扭曲爱德华曲线形式

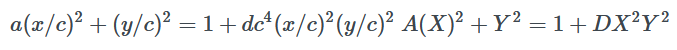
然后，我们需要把扭曲爱德华曲线映射为蒙哥马利曲线，再用蒙哥马利曲线映射到 Weierstrass 曲线。

映射后，我们分析曲线的阶和点的阶，会发现符合Pohlig-Hellman的攻击方式。

exp：

#sage
import gmpy2
from Crypto.Util.number import *

p = 101194790049284589034264952247851014979689350430642214419992564316981817280629
a = 73101304688827564515346974949973801514688319206271902046500036921488731301311
c = 78293161515104296317366169782119919020288033620228629011270781387408756505563
d = 37207943854782934242920295594440274620695938273948375125575487686242348905415
P.<z> = PolynomialRing(Zmod(p))

aa = a
dd = (d*c^4)%p
J = (2*(aa+dd)*gmpy2.invert(aa-dd,p))%p
K = (4*gmpy2.invert(aa-dd,p))%p
A = ((3-J^2)*gmpy2.invert(3*K^2,p))%p
B = ((2*J^3-9*J)*gmpy2.invert(27*K^3,p))%p

for i in  P(z^3+A*z+B).roots():
    alpha = int(i[0])
    print(kronecker(3*alpha^2+A,p))
    for j in P(z^2-(3*alpha^2+A)).roots():
        s = int(j[0])
        s = inverse_mod(s, p)
        if J==alpha*3*s%p:
            Alpha = alpha
            S = s

def twist_to_weier(x,y):
    v = x*gmpy2.invert(c,p)%p
    w = y*gmpy2.invert(c,p)%p
    assert (aa*v^2+w^2)%p==(1+dd*v^2*w^2)%p
    s = (1+w)*inverse_mod(1-w,p)%p
    t = s*gmpy2.invert(v,p)%p
    assert (K*t^2)%p==(s^3+J*s^2+s)%p
    xW = (3*s+J) * inverse_mod(3*K, p) % p
    yW = t * inverse_mod(K, p) % p
    assert yW^2 % p == (xW^3+A*xW+B) % p
    return (xW,yW)

def weier_to_twist(x,y):
    xM=S*(x-Alpha)%p
    yM=S*y%p
    assert (K*yM^2)%p==(xM^3+J*xM^2+xM)%p
    xe = xM*inverse_mod(yM,p)%p
    ye = (xM-1)*inverse_mod(xM+1,p)%p
    assert (aa*xe^2+ye^2)%p==(1+dd*xe^2*ye^2)%p
    xq = xe*c%p
    yq = ye*c%p
    assert (a*xq^2+yq^2)%p==c^2*(1+d*xq^2*yq^2)
    return (xq,yq)

E = EllipticCurve(GF(p), [A, B])
G = twist_to_weier(30539694658216287049186009602647603628954716157157860526895528661673536165645,64972626416868540980868991814580825204126662282378873382506584276702563849986)
Q = twist_to_weier(98194560294138607903211673286210561363390596541458961277934545796708736630623,58504021112693314176230785309962217759011765879155504422231569879170659690008)
P = E(G)
Q = E(Q)
factors, exponents = zip(*factor(E.order()))
primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-2]
print(primes)
dlogs = []
for fac in primes:
    t = int(int(P.order()) // int(fac))
    dlog = discrete_log(t*Q,t*P,operation="+")
    dlogs += [dlog]
    print("factor: "+str(fac)+", Discrete Log: "+str(dlog)) #calculates discrete logarithm for each prime order
flag=crt(dlogs,primes)
print(long_to_bytes(flag))
#Tw1stzzzz

dp_promax

from Crypto.Util.number import *
from random import *

nbits = 2200
beta = 0.4090
p, q = getPrime(int((1. - beta) * nbits)), getPrime(int(beta * nbits))
dp = getrandbits(50) | 1
while True:
    d = (p - 1) * getrandbits(2800) + dp
    if GCD((p - 1) * (q - 1), d) == 1:
        break
e = inverse(d, (p - 1) * (q - 1))
N = p * q
flag = bytes_to_long(open('flag.txt', 'rb').read())

c = pow(flag, e, N)
print(N)
print(e)
print(c)

"""
46460689902575048279161539093139053273250982188789759171230908555090160106327807756487900897740490796014969642060056990508471087779067462081114448719679327369541067729981885255300592872671988346475325995092962738965896736368697583900712284371907712064418651214952734758901159623911897535752629528660173915950061002261166886570439532126725549551049553283657572371862952889353720425849620358298698866457175871272471601283362171894621323579951733131854384743239593412466073072503584984921309839753877025782543099455341475959367025872013881148312157566181277676442222870964055594445667126205022956832633966895316347447629237589431514145252979687902346011013570026217
13434798417717858802026218632686207646223656240227697459980291922185309256011429515560448846041054116798365376951158576013804627995117567639828607945684892331883636455939205318959165789619155365126516341843169010302438723082730550475978469762351865223932725867052322338651961040599801535197295746795446117201188049551816781609022917473182830824520936213586449114671331226615141179790307404380127774877066477999810164841181390305630968947277581725499758683351449811465832169178971151480364901867866015038054230812376656325631746825977860786943183283933736859324046135782895247486993035483349299820810262347942996232311978102312075736176752844163698997988956692449
28467178002707221164289324881980114394388495952610702835708089048786417144811911352052409078910656133947993308408503719003695295117416819193221069292199686731316826935595732683131084358071773123683334547655644422131844255145301597465782740484383872480344422108506521999023734887311848231938878644071391794681783746739256810803148574808119264335234153882563855891931676015967053672390419297049063566989773843180697022505093259968691066079705679011419363983756691565059184987670900243038196495478822756959846024573175127669523145115742132400975058579601219402887597108650628746511582873363307517512442800070071452415355053077719833249765357356701902679805027579294
"""

直接分解n

from Crypto.Util.number import *
import gmpy2 

p=3628978044425516256252147348112819551863749940058657194357489608704171827031473111609089635738827298682760802716155197142949509565102167059366421892847010862457650295837231017990389942425249509044223464186611269388650172307612888367710149054996350799445205007925937223059
q=12802692475349485610473781287027553390253771106432654573503896144916729600503566568750388778199186889792482907407718147190530044920232683163941552482789952714283570754056433670735303357508451647073211371989388879428065367142825533019883798121260838408498282273223302509241229258595176130544371781524298142815099491753819782913040582455136982147010841337850805642005577584947943848348285516563
n=46460689902575048279161539093139053273250982188789759171230908555090160106327807756487900897740490796014969642060056990508471087779067462081114448719679327369541067729981885255300592872671988346475325995092962738965896736368697583900712284371907712064418651214952734758901159623911897535752629528660173915950061002261166886570439532126725549551049553283657572371862952889353720425849620358298698866457175871272471601283362171894621323579951733131854384743239593412466073072503584984921309839753877025782543099455341475959367025872013881148312157566181277676442222870964055594445667126205022956832633966895316347447629237589431514145252979687902346011013570026217
e=13434798417717858802026218632686207646223656240227697459980291922185309256011429515560448846041054116798365376951158576013804627995117567639828607945684892331883636455939205318959165789619155365126516341843169010302438723082730550475978469762351865223932725867052322338651961040599801535197295746795446117201188049551816781609022917473182830824520936213586449114671331226615141179790307404380127774877066477999810164841181390305630968947277581725499758683351449811465832169178971151480364901867866015038054230812376656325631746825977860786943183283933736859324046135782895247486993035483349299820810262347942996232311978102312075736176752844163698997988956692449
c=28467178002707221164289324881980114394388495952610702835708089048786417144811911352052409078910656133947993308408503719003695295117416819193221069292199686731316826935595732683131084358071773123683334547655644422131844255145301597465782740484383872480344422108506521999023734887311848231938878644071391794681783746739256810803148574808119264335234153882563855891931676015967053672390419297049063566989773843180697022505093259968691066079705679011419363983756691565059184987670900243038196495478822756959846024573175127669523145115742132400975058579601219402887597108650628746511582873363307517512442800070071452415355053077719833249765357356701902679805027579294

phi = (p-1)*(q-1)
d=gmpy2.invert(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))
#nctf{Th1s_N_May_n0t_s0@o0@@_secur3}

coloratura

from Crypto.Util.number import long_to_bytes
from PIL import Image, ImageDraw
from random import getrandbits

width = 208
height = 208
flag = open('flag.txt').read()

def makeSourceImg():
    colors = long_to_bytes(getrandbits(width * height * 24))[::-1]
    img = Image.new('RGB', (width, height))
    x = 0
    for i in range(height):
        for j in range(width):
            img.putpixel((j, i), (colors[x], colors[x + 1], colors[x + 2]))
            x += 3
    return img

def makeFlagImg():
    img = Image.new("RGB", (width, height))
    draw = ImageDraw.Draw(img)
    draw.text((5, 5), flag, fill=(255, 255, 255))
    return img

if __name__ == '__main__':
    img1 = makeSourceImg()
    img2 = makeFlagImg()
    img3 = Image.new("RGB", (width, height))
    for i in range(height):
        for j in range(width):
            p1, p2 = img1.getpixel((j, i)), img2.getpixel((j, i))
            img3.putpixel((j, i), tuple([(p1[k] ^ p2[k]) for k in range(3)]))
    img3.save('attach.png')

这是一道经典的MT19937题。

看到本题取随机数的函数为 colors = long_to_bytes(getrandbits(width * height * 24))[::-1]，通过测试我们可以知道，getrandbits函数在收到超出32比特的参数，会把已生成的state放在低位，高位放置新生成的state。这里倒序则是把state0放在了最开始。

注意到draw.text((5, 5), flag, fill=(255, 255, 255))，flag填充的位置在5,5。所以我们有4行未经过异或的原值，其比特数为208∗4∗24=32∗624  ，刚好有624组state，然后我们就可以依次生成后续的内容得到原图，异或之后得到flag图像。

exp:

from PIL import Image
import random
from Crypto.Util.number import *

def invert_right(m, l, val=''):
    length = 32
    mx = 0xffffffff
    if val == '':
        val = mx
    i, res = 0, 0
    while i * l < length:
        mask = (mx << (length - l) & mx) >> i * l
        tmp = m & mask
        m = m ^ tmp >> l & val
        res += tmp
        i += 1
    return res

def invert_left(m, l, val):
    length = 32
    mx = 0xffffffff
    i, res = 0, 0
    while i * l < length:
        mask = (mx >> (length - l) & mx) << i * l
        tmp = m & mask
        m ^= tmp << l & val
        res |= tmp
        i += 1
    return res

def invert_temper(m):
    m = invert_right(m, 18)
    m = invert_left(m, 15, 4022730752)
    m = invert_left(m, 7, 2636928640)
    m = invert_right(m, 11)
    return m

def clone_mt(record):
    state = [invert_temper(i) for i in record]
    gen = random.Random()
    gen.setstate((3, tuple(state + [0]), None))
    return gen

def makeSourceImg():
    colors = long_to_bytes(g.getrandbits(width * height * 24))[::-1]
    img = Image.new('RGB', (width, height))
    x = 0
    for i in range(height):
        for j in range(width):
            img.putpixel((j, i), (colors[x], colors[x + 1], colors[x + 2]))
            x += 3
    return img

height, width = 208, 208

img = Image.open('attach.png')
a = []
for i in range(4):
    for j in range(208):
        p = img.getpixel((j, i))
        for pi in p:
            a.append(pi)
M = []
for i in range(len(a) // 4):
    px = (a[4 * i + 3] << 24) + (a[4 * i + 2] << 16) + (a[4 * i + 1] << 8) + a[4 * i + 0]
    M.append(px)

g = clone_mt(M)

img1 = makeSourceImg()
img2 = Image.open('attach.png')
img3 = Image.new("RGB", (width, height))
for i in range(height):
    for j in range(width):
        p1, p2 = img1.getpixel((j, i)), img2.getpixel((j, i))
        img3.putpixel((j, i), tuple([(p1[k] ^ p2[k]) for k in range(3)]))
img3.save('flag.png')