codeforce 626E(二分）

E. Simple Skewness

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Define the simple skewness of a collection of numbers to be the collection's mean minus its median. You are given a list of n (not necessarily distinct) integers. Find the non-empty subset (with repetition) with the maximum simple skewness.

The mean of a collection is the average of its elements. The median of a collection is its middle element when all of its elements are sorted, or the average of its two middle elements if it has even size.

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 200 000) — the number of elements in the list.

The second line contains n integers x_i (0 ≤ x_i ≤ 1 000 000) — the ith element of the list.

Output

In the first line, print a single integer k — the size of the subset.

In the second line, print k integers — the elements of the subset in any order.

If there are multiple optimal subsets, print any.

Examples

Input

4

1 2 3 12

Output

3

1 2 12 

Input

4

1 1 2 2

Output

3

1 1 2 

Input

2

1 2

Output

2

1 2

Note

In the first case, the optimal subset is 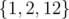, which has mean 5, median 2, and simple skewness of 5 - 2 = 3.

In the second case, the optimal subset is 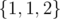. Note that repetition is allowed.

In the last case, any subset has the same median and mean, so all have simple skewness of 0.

题意：给你n个数，让你从里面任选若干个数，使得这些数的平均值 - 中位数 最大。

分析：

先将原序列从小到大排序，再枚举中位数，求每一个中位数的最大平均数

子序列的长度一定是奇数，当个数由奇数个变成偶数个时，中位数增加的比平均数增加的要多，（平均数-中位数）的值就会变小

针对每一个中位数，二分总长度的长度的一半len，找到最大的平均数。

中位数是arr[i]，长度的一半为len时，为了使平均数尽可能的大，找到的子序列一定是：arr[i-len]……arr[i] && arr[n-len+1]……arr[n]（arr[]从1开始）

当len+1时，子序列中将增加arr[i-len-1]和arr[n-len]，增加的数是减小的，所以随着len的增加，平均数总的来说应该是先增大再减小的，所以可以用二分求len

 #include <iostream>
 #include <algorithm>
 #include <cstdio>
 #include <cstring>
 using namespace std;
 typedef long long LL;
 const int Max =  + ;
 LL arr[Max],sum[Max];
 int main()
 {
     int n;
     scanf("%d", &n);
     sum[] = ;
     for(int i = ; i <= n; i++)
     {
         scanf("%I64d", &arr[i]);
         sum[i] = sum[i - ] + arr[i];
     }
     int res,pos = ,len = ;
     double maxRes = -;
     for(int i = ; i <= n; i++)
     {
         int l = , r = min(i - , n - i);
         res = ;
         while(r >= l)
         {
             int mid = (l + r) >> ;
             double mean1 = 1.0 * (sum[i] - sum[i - mid - ] + sum[n] - sum[n - mid]) / ( * mid + );
             double mean2 = 1.0 * (sum[i] - sum[i - mid] + sum[n] - sum[n - mid + ]) / (  * (mid - ) + );
             if(mean1 > mean2)  //与前一个进行比较，如果比前一个大左边就往前移，否则往右移，因为平均数是先变大后变小的通过与前面的比较找到最大的那个；
             {
                 res = mid;
                 l = mid + ;
             }
             else
             {
                 r = mid - ;
             }
         }
         double ans = 1.0 * (sum[i] - sum[i - res - ] + sum[n] - sum[n - res]) / ( * res + ) - arr[i];
         if(ans > maxRes)
         {
             maxRes = ans;
             pos = i;
             len = res;
         }
     }
     printf("%d\n",  * len + );
    //题目对输出要求不严格，相同的结果随便输出
     for(int i = pos - len; i < pos; i++)
         printf("%I64d ", arr[i]);
     for(int i = n - len + ; i <= n; i++)
         printf("%I64d ", arr[i]);
     printf("%I64d\n", arr[pos]);

     return ;
 }