ZOJ 2753 Min Cut (Destroy Trade Net)（无向图全局最小割）

题目大意

给一个无向图，包含 N 个点和 M 条边，问最少删掉多少条边使得图分为不连通的两个部分，图中有重边

数据范围：2<=N<=500, 0<=M<=N*(N-1)/2

做法分析

典型的无向图全局最小割，使用 Stoer-Wagner 算法

Stoer-Wagner 算法共执行 n-1 次 BFS，每次 BFS 得到一个当前图的最小 S-T 割，并且将最后 BFS 的两个点缩点，n-1 次 BFS 得到 n-1 个最小 S-T 割中的最小者就是整个无向图的全局最小割，为了讲述每次 BFS 执行的操作，先进行如下定义：

　　令 g[i][j] 表示边 (i, j) 的权值，对于无向图，我们有 g[i][j]=g[j][i]

　　令 w[u] 表示 u 和已经被 BFS 过的点的关联度，即 w[u]=∑g[v][u] 其中，v 是已经被 BFS 过的点，u 是未被 BFS 的点。初始时，所有点的 w 值全部为 0

　　令 vs[u] 表示 u 是否已经被 BFS 过，vs[u]=1 表示 u 已经被 BFS 过。初始时，所有点的 vs 值全部为 0

每次 BFS 按如下步骤执行：

　　1. 选出未被 BFS 过的点中，关联度（w 值）最大的点（如果有多个，任选一个），设为 u。如果所有的点都已经被 BFS 过，则退出当前 BFS 过程

　　2. 用 u 更新所有未被 BFS 的点的关联度，即： w[v]+=g[u][v]，其中 v 没有被 BFS 过

　　3. 将 u 设置为 BFS 过，即将 vs[u] 的值由 0 变为 1

　　设倒数第 2 个被 BFS 的点为 S，倒数第 1 个被 BFS 的点为 T，那么，w[T] 就是本次 BFS 得到的最小 S-T 割

每次 BFS 后，将最后 BFS 的两个点 S 和 T 缩成一个点 u，即：g[i][u]=g[i][S]+g[i][T]

每次 BFS 后，用得到的最小 S-T 割更新全局的最小割

n-1 次 BFS 后，全局最小割求出来了，图也被缩成了一个点

下面是一个例子

假设在进行 BFS 时有一个无向图如下：

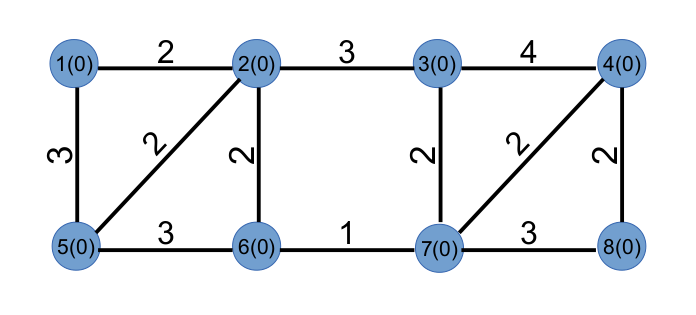
图中，括号中的数字表示每个点的 w 值，初始化为 0，边上的值表示边权。现在选择一个具有最大关联度（w 值最大）的点，有多种选择时随意选取一个点，假设选取的是第 2 个点，将它标记为已经访问过的点，并更新其他未被访问过的点的关联度：

现在，第 3 个点的关联度最大，选它作为下一个 BFS 的点，将它标记为已经访问过的点，并用它更新其他未被访问过的点的关联度：

第 4 个点的关联度最大，选其作为下一个 BFS 的点，将它标记为已经访问过的点，并更新其他未被访问过的点的关联度：

第 7 个点的关联度最大，选其作为下一个 BFS 的点，将它标记为已经访问过的点，并更新其他未被访问过的点的关联度：

第 8 个点的关联度最大，选其作为下一个 BFS 的点，将它标记为已经访问过的点，并更新其他未被访问过的点的关联度：

第 6 个点的关联度最大，选其作为下一个 BFS 的点，将它标记为已经访问过的点，并更新其他未被访问过的点的关联度：

第 5 个点的关联度最大，选其作为下一个 BFS 的点，将它标记为已经访问过的点，并更新其他未被访问过的点的关联度：

第 1 个点的关联度最大，选其作为下一个 BFS 的点，将它标记为已经访问过的点，并更新其他未被访问过的点的关联度：

至此，所有的点都被 BFS 了一遍，最后访问的点是 1，倒数第二访问的点是 5：

那么，我们这次 BFS 的 S 点是 5，T 点是 1，这次 BFS 得到的最小 S-T 割为 w[T]=5（上图中绿色的点）

将 S 点和 T 点合并：

得到新图：

将所有的标记（包括关联度，是否访问过）清空，进行下一次 BFS ，直至所有的点缩成一个点为止：

这样，经过 n-1 次 BFS 之后，整个无向图的全局最小割就求出来了

时间复杂度不难分析：o(n^3)

但是，我想，如果在每次 BFS 的时候，就像 Dijkstra 一样用堆优化，应该可以把复杂度降低到 o(n^2log₂(n))

详细证明，请看 A Simple Min-Cut Algorithm

参考代码

 #include <iostream>
 #include <cstdio>
 #include <cstring>

 using namespace std;

 struct Stoer_Wagner {
     static const int N=, INF=(<<);
     int G[N][N], W[N], Merge[N], S, T, minCut, n;
     bool vs[N];

     void init(int _n) {
         n=_n;
         memset(G, , sizeof G);
     }

     void BFS() {
         memset(vs, , sizeof vs);
         memset(W, , sizeof W);
         S=T=-;
         int Max, id;
         for(int cnt=; cnt<n; cnt++) {
             Max=-INF;
             for(int i=; i<n; i++)
                 if(!Merge[i] && !vs[i] && W[i]>Max)
                     Max=W[i], id=i;
             if(id==T) return;
             S=T, T=id;
             minCut=Max;
             vs[id]=;
             for(int i=; i<n; i++) {
                 if(Merge[i] || vs[i]) continue;
                 W[i]+=G[id][i];
             }
         }
     }

     int StoerWagner() {
         memset(Merge, , sizeof Merge);
         int ans=INF;
         for(int cnt=; cnt<n; cnt++) {
             BFS();
             if(minCut<ans) ans=minCut;
             if(ans==) return ans;
             Merge[T]=;
             for(int i=; i<n; i++) {
                 if(Merge[i]) continue;
                 G[S][i]+=G[T][i];
                 G[i][S]+=G[i][T];
             }
         }
         return ans;
     }
 };

 Stoer_Wagner fuck;
 int n, m;

 int main() {
     while(scanf("%d%d", &n, &m)!=EOF) {
         fuck.init(n);
         for(int i=, a, b, c; i<m; i++) {
             scanf("%d%d%d", &a, &b, &c);
             fuck.G[a][b]+=c;
             fuck.G[b][a]+=c;
         }
         printf("%d\n", fuck.StoerWagner());
     }
     return ;
 }

ZOJ 2753

题目链接 & AC 通道

ZOJ 2753 Min Cut (Destroy Trade Net)