Ceres 四重奏 之 入门简介

Ceres 翻译为谷神星，是太阳系中的一颗矮行星，于1801年被意大利神父 Piazzi 首次观测到，但随后 Piazzi 因为生病，跟丢了它的运行轨迹。

几个月后，德国数学家 Gauss，利用最小二乘法，仅仅依靠 Piazzi 之前观测到的12个数据，便成功的预测了谷神星的运行轨迹。

两百多年后，为了解决一些复杂的最优化问题 (如：带边界约束的非线性最小二乘、一般的无约束最优化等)，谷歌开发了一个 C++ 库 Ceres Solver

之所以取名 Ceres Solver，是为了纪念 Gauss 利用最小二乘法，成功的预测了谷神星轨迹，这个在最优化、统计学、天文学历史上，都具有重要意义的事件

1  Ceres 简介

1.1  特点

1) 模型接口简洁

- 求导简单；鲁棒的损失函数；局部参数化

2) 求解方法多

- 信赖域法：Lenberg-Marquardt, Powell’s Dogleg, Subspace dogleg

- 线搜索法：Non-linear Conjugate Gradients, BFGS, LBFGS

3) 求解质量高

- 在 NIST 数据集下，按照 Mondragon 和 Borchers 的测试标准，Ceres 的准确度最高

1.2  应用

在谷歌内部，Ceres 已经被应用于多个产品中，如：谷歌街景中汽车、飞行器的位姿估计；PhotoTours 中 3D 模型的建立；SLAM 算法 Cartographer 等

此外，一些公司和研究所也在使用 Ceres，像是 Southwest Research Institute 的机器人视觉系统标定，OpenMVG 的光束平差 (BA) 问题，Willow Garage 的 SLAM 问题等

1.3  非线性最小二乘

带边界约束的非线性最小二乘形式，如下：

$\quad \begin{split} \min_x &\quad \frac{1}{2}\sum_{i} \rho_i\left(\left\|f_i\left(x_{i_1}, x_{i_2}, ... ,x_{i_k}\right)\right\|^2\right) \\\text{s.t.} &\quad l_j \le x_j \le u_j \end{split}$

其中，1) s.t. = "subject to"，限定了 $x_j$ 的取值范围

2) $ \rho_i\left(\left\|f_i\left(x_{i_1},x_{i_2},...,x_{i_k}\right)\right\|^2\right) $ 为残差块

3) $f_i(\cdot)$ 为代价函数，取决于参数块 $\left[x_{i_1},x_{i_2},... , x_{i_k}\right]$

4) $\rho_i$ 为损失函数，是一个标量函数，主要用来消除异常点对求解过程的影响

如果令损失函数 $\rho_i = x$ 为恒等函数，且放宽边界约束条件为 $[-\infty, \infty]$

则非线性最小二乘问题，可简化为如下形式：

$\quad \begin{split}\frac{1}{2}\sum_{i} \left\|f_i\left(x_{i_1}, ... ,x_{i_k}\right)\right\|^2 \end{split}$

上面的最小二乘形式，在科学和工程领域有着广泛的应用，例如，统计学中的曲线拟合，计算机视觉的三维重建等

2  编译配置

Win10  64-bit ；VS 2019 社区版，下载地址 ；CMake 解压版，下载地址

2.1  源文件

- Ceres Solver 源文件，下载地址，从 2.0 开始，需要支持 C++14 的编译器

- eigen 源文件，必须，>=3.3，下载地址

- glog 源文件，推荐，>=0.3.1，下载地址，及其依赖库 gflags，下载地址

2.2  配置生成

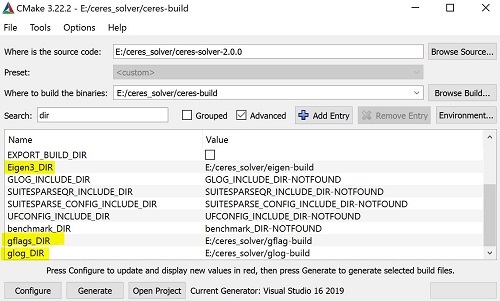
1)  将源文件 ceres、eigen、glog 和 gflags 解压，运行 cmake-gui.exe，配置生成 eigen (先点 "Configure"，再点 "Generate" 即可)

2)  编译 gflags，先点 "Configure"，再点 "Generate"，然后点 "Open Project"，在 VS 中打开工程，最后在 debug 和 release 模式下分别编译

3)  编译 glog，操作同 3)，其中 cmake 配置不再赘述，如：CMAKE_CONFGURATION_TYPES 只保留 Debug 和 Release，gflags_DIR 指向含 gflags-config.cmake 的目录等

4)  编译 ceres，操作同 3)，注意配置 eigen、glog 和 gflags 的 _DIR 目录，并勾上 BUILD_SHARED_LIBS 以便生成 dll 库

2.3  VS 配置

将生成的 .lib 和 .dll 文件放在特定目录下，并新建 include 文件夹，汇总对应的 .h 文件

  1）环境变量

计算机 -> 属性 -> 高级系统设置 -> 环境变量，编辑系统变量里的 path 变量

D:\3rdparty\gflags\bin\Debug
D:\3rdparty\glog\bin\Debug
D:\3rdparty\ceres\bin\Debug　　

  2)  头文件和库文件

在 VS 中配置 ceres, eigen, glog 和 gflags 的 头文件目录，以及 库文件目录

注：在编译时，若出现头文件缺失，则在源文件中找到对应的 .h，拷贝到 include 目录中即可

  3)  依赖库

添加对应的 .lib 依赖库，如下：

ceres-debug.lib
gflags_debug.lib
glogd.lib

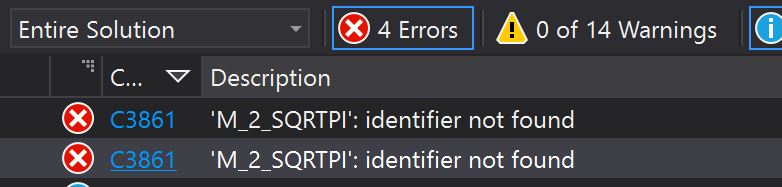
  4)  错误处理

运行程序，如出现如下错误，则在 "项目属性 - 预处理器定义" 中，定义 _USE_MATH_DEFINES 宏可解决

3  代码实例

给定一个目标函数 $\begin{split} \frac{1}{2}(10 -x)^2 \end{split}$，求其取最小值时，对应的 $x$ 为多少

3.1  求解步骤

    1)  构建代价函数

Ceres 中利用仿函数，通过重载 operator() 运算符，来实现代价函数的定义，本例中的代价函数为 $f(x) = 10 -x $

// A templated cost functor that implements the residual r = x - 10
struct CostFunctor {
    template <typename T> bool operator()(const T* const x, T* residual) const {
        residual[0] = x[0] - 10.0;
        return true;
    }
};　　

    2)  构建残差块

   // Build the problem
    Problem problem;
    // Set up the cost function (also known as residual)
    CostFunction* cost_function = new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
    problem.AddResidualBlock(cost_function, NULL, &x);　　

    3)  配置求解器

    // The options structure, which controls how the solver operates
    Solver::Options options;
    options.linear_solver_type = ceres::DENSE_QR;
    options.minimizer_progress_to_stdout = true;　　

    4)  求解

    // Run the solver
    Solver::Summary summary;
    Solve(options, &problem, &summary);

3.2  完整代码    　　

#include "ceres/ceres.h"

using ceres::AutoDiffCostFunction;
using ceres::CostFunction;
using ceres::Problem;
using ceres::Solver;
using ceres::Solve;

// A templated cost functor that implements the residual r = x - 10.
struct CostFunctor {
    template <typename T> bool operator()(const T* const x, T* residual) const {
        residual[0] = 10.0 - x[0];
        return true;
    }
};

int main()
{
    // The variable to solve for with its initial value
    double x = 0.5;
    const double initial_x = x;

    // Build the problem.
    Problem problem;
    // Set up the cost function (also known as residual)
    CostFunction* cost_function = new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
    problem.AddResidualBlock(cost_function, NULL, &x);

    // The options structure, which controls how the solver operates
    Solver::Options options;
    options.linear_solver_type = ceres::DENSE_QR;
    options.minimizer_progress_to_stdout = true;

    // Run solver
    Solver::Summary summary;
    Solve(options, &problem, &summary);

    std::cout << summary.BriefReport() << "\n";
    std::cout << "x : " << initial_x << " -> " << x << "\n";
}　　

运行结果如下：

参考资料

Ceres Solver 在 Windows 下的安装

Mondragon 和 Borchers 标准对比测试