额外空间复杂度O(1) 的二叉树遍历 → Morris Traversal,你造吗?
开心一刻
一天,有个粉丝遇到感情方面的问题,找我出出主意
粉丝:我女朋友吧,就是先天有点病,听不到人说话,也说不了话,现在我家里人又给我介绍了一个,我该怎么办
我:这个问题很难去解释,我觉得一个人活着,他要对身边的人负责,对家人负责,对自己负责
从语音中我能感受得到粉丝很难受,我继续补充
我:我不是说让你放弃掉你的女朋友,你们一定是有一定的感情基础才在一起的,但你还是需要衡量衡量你的未来
我能明显感觉到粉丝已经在抽泣,继续说道
我:当然,这个时候离开肯定是不合适的,对吧?
粉丝:是的
我:这种感情的问题,我很难说让你怎么样,这个只有你自己去衡量,找到一个最合适的解决办法
粉丝哭泣到:我真的不知道怎么办
我最不忍心看别人哭,安慰道:你先别哭,问题总有办法解决的,哭不是解决问题的办法,你先平复下
过了一会,粉丝说道:我知道了,我还是遵从家里的意见吧,给我现在的女朋友气放了
我:女朋友气... 我放你个大乌龟

前情回顾
二叉树的遍历 → 不用递归,还能遍历吗中讲到了二叉树的深度遍历的实现方式:递归、栈+迭代
不管采用何种方式,额外空间复杂度都是 O(N)
那有没有额外空间复杂度 O(1) 的遍历方式了?
很早之前就被人给专研出来了,也就是本文的主角:Morris Traversal
Morris Traversal
因为它由 Joseph Morris 发明的,所以叫 Morris Traversal
递归、栈+迭代的遍历,本质都是使用了栈结构进行辅助,所以在处理完某个节点后能回到上层去
二叉树的结构决定了它从上层到下层(根到叶子)很容易,但从下层到上层却很难,因为只有父节点指向子节点的指针,而没有子节点指向父节点的指针
Morris 遍历的实质就是避免使用栈结构,而是让下层到上层有指针,通过底层节点指向 null 的空闲指针指向上层的某个节点,从而实现下层到上层的移动
空闲指针从哪来?二叉树的叶子节点,或者只有单个孩子的节点(左指针空闲或右指针空闲)
具体实现,我们往下看
移动规则
也就是遍历过程;设当前节点为 cur ,初始 cur = root ,则 cur 的移动规则如下
1、如果 cur 没有左子树,则让 cur 向右移动,即 cur = cur.right
2、如果 cur 有左子树,则找到 cur 左子树最右的节点,记作 mostRight
2.1、如果 mostRight 的右指针指向 null ,让其指向 cur ,然后 cur 向左移动

2.2、如果 mostRight 的右指针指向 cur ,让其指向 null ,然后 cur 向右移动

3、当 cur 为 null 时,遍历停止
这描述还是有点抽象,我们结合具体的二叉树,利用移动规则把二叉树遍历一遍
初始二叉树如下

1)初始 cur 在节点 a,此时 cur 有左子树,找到其左子树的最右节点,即节点 k,k 的右指针指向 null ,让其指向 cur ,然后 cur 左移
此时二叉树结构如下, cur 第一次来到节点 b
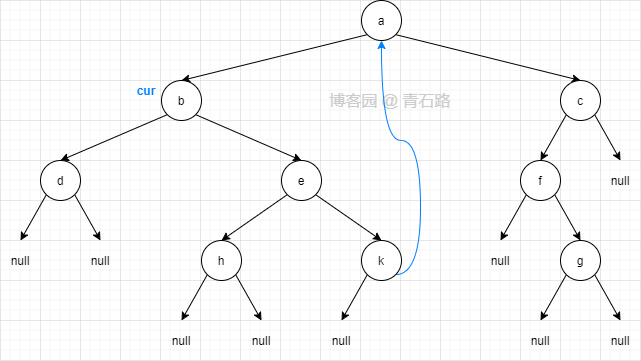
2)此时 cur 在节点 b, cur 有左子树,找到其左子树的最右节点,即节点 d,d 的右指针指向 null ,让其指向 cur ,然后 cur 左移
此时二叉树结构如下, cur 第一次来到节点 d
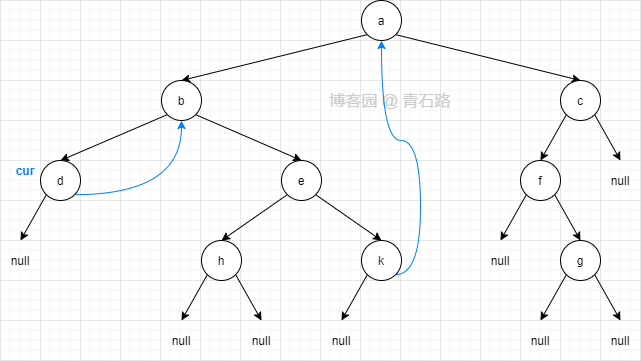
3)此时 cur 在节点 d,cur 没有左子树, cur 右移
此时二叉树结构如下, cur 第二次来到节点 b
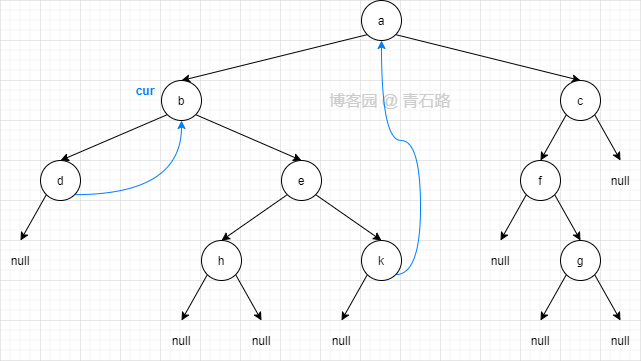
4)此时 cur 在节点 b, cur 有左子树,找到其左子树的最右节点,即节点 d,d 的右指针指向 cur ,让其指向 null ,然后 cur 右移
此时二叉树结构如下, cur 第一次来到节点 e
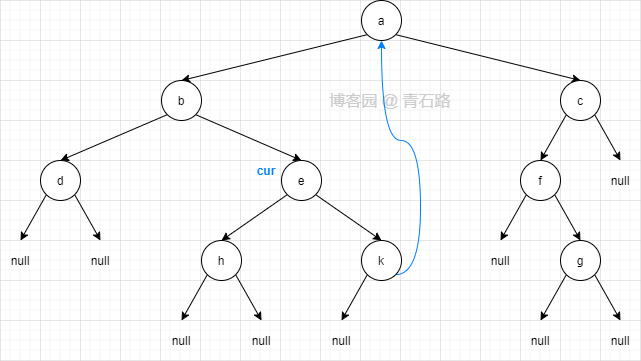
这里大家可能会有疑问:找 cur 的左子树的最右节点时,找到的不应该是节点 c 吗?
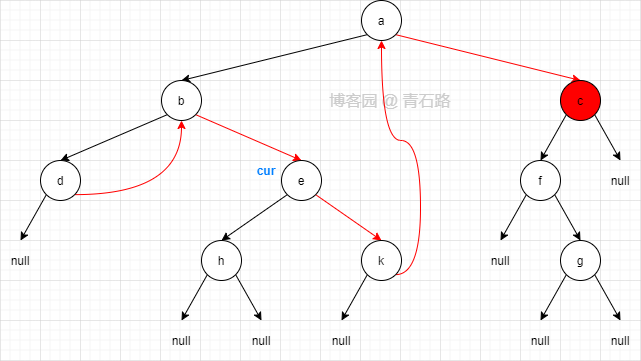
所以这里有细节要处理,找左子树最右节点的时候,遇到两种情况(右指针指向 null 或右指针指向 cur )都需要停止寻找,用代码描述就是:

5)此时 cur 在节点 e, cur 有左子树,找到其左子树的最右节点,即节点 h,h 的右指针指向 null ,让其指向 cur ,然后 cur 左移
此时二叉树结构如下, cur 第一次来到节点 h
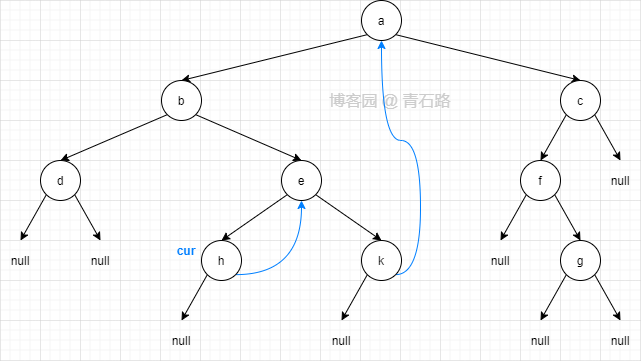
6)此时 cur 在节点 h, cur 没有左子树, cur 右移
此时二叉树结构如下, cur 第二次来到节点 e
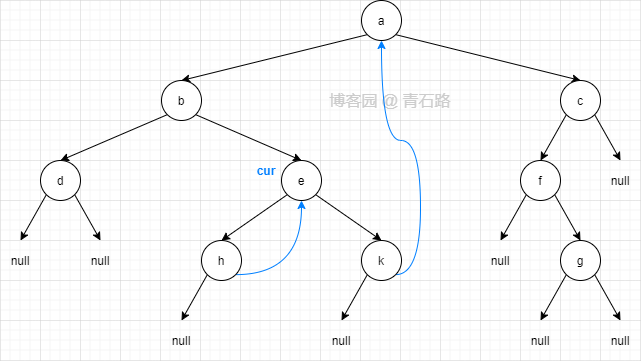
7)此时 cur 在节点 e, cur 有左子树,找到其左子树的最右节点,即节点 h,h 的右指针指向 cur ,让其指向 null ,然后 cur 右移
此时二叉树结构如下, cur 第一次来到节点 k
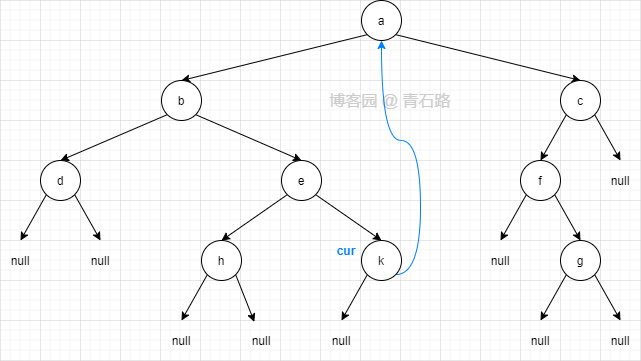
8)此时 cur 在节点 k, cur 没有左子树, cur 右移
此时二叉树结构如下, cur 第二次来到节点 a(为什么是第二次?因为最初从 a 开始的)
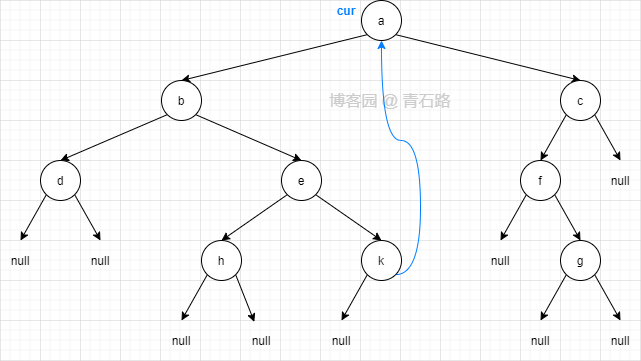
9)此时 cur 在节点 a, cur 有左子树,找到其左子树的最右节点,即节点 k,k 的右指针指向 cur ,让其指向 null ,然后 cur 右移
此时二叉树结构如下, cur 第一次来到节点 c

10)此时 cur 在节点 c, cur 有左子树,找到其左子树的最右节点,即节点 g,g 的右指针指向 null ,让其指向 cur ,然后 cur 左移
此时二叉树结构如下, cur 第一次来到节点 f

11)此时 cur 在节点 f, cur 没有左子树, cur 右移
此时二叉树结构如下, cur 第一次来到节点 g

12)此时 cur 在节点 g, cur 没有左子树, cur 右移
此时二叉树结构如下, cur 第二次来到节点 c

13)此时 cur 在节点 c, cur 有左子树,找到其左子树的最右节点,即节点 g,g 的右指针指向 cur ,让其指向 null , cur 右移
此时二叉树结构如下, cur = null

14)此时 cur 为 null ,遍历停止
可以看到,二叉树回到了最初的状态,最终结构与最初一致
前面步骤有点长,看的可能不够直观,我们来看个完整版的
上述的遍历就是 Morris Traversal , cur 所经历的节点 a -> b -> d -> b -> e -> h -> e -> k -> a -> c -> f -> g -> c 组成了 Morris 序
在遍历的过程中,相信大家已经得出一个规律:有左子树的节点(b、e、a、c)会到达两次,没有左子树的节点(d、h、k、f、g)则只会到达一次
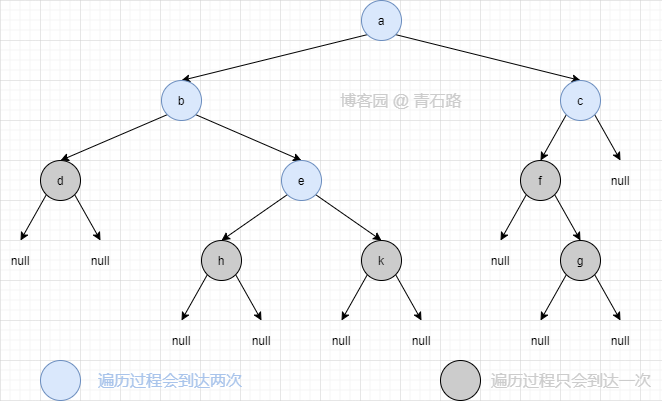
这绝对不是巧合啊!这是 Morris Traversal 移动规所产生的必然结果
对于那些能达到两次的节点,我们如何区分是第一次到达,还是第二次到达?
在上述的遍历过程中,相信大家已经找到答案了
1、如果其左子树的最右节点指向 null ,即 mostRight.right = null ,则该节点是第一次到达
2、如果其左子树的最右节点指向自身,即 mostRight.right = cur ,则该节点是第二次到达
经过了上述诸多的准备, Morris Traversal 代码实现就非常简单了
代码实现

相信大家都能看懂这个代码,没看懂的再去把前面的遍历过程再看看
Morris Traversal 一定要看懂,不然后面的深度遍历就玩不动了
先序遍历

我们对比下 先序序列 和 Morris 序列
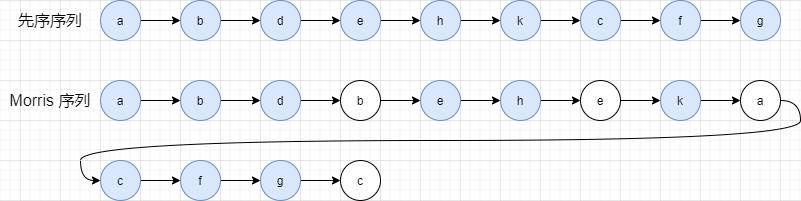
发现了什么? Morris Traversal 第二次到达的节点不打印,就是 先序序列 了
代码也就手到擒来了

中序遍历

我们对比下 中序序列 和 Morris 序列
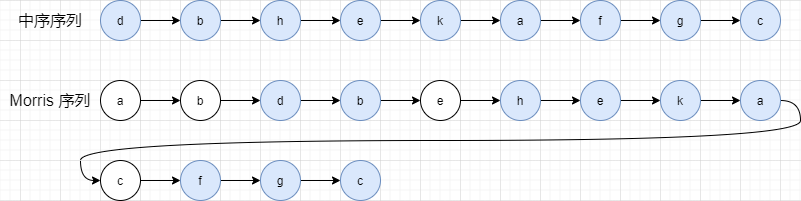
只会遍历一次的节点,直接打印;会遍历两次的节点,第一次的时候不打印,第二次打印,就得到了 中序序列
代码很容易撸出来了

后序遍历

对比 后序序列 和 Morris 序列
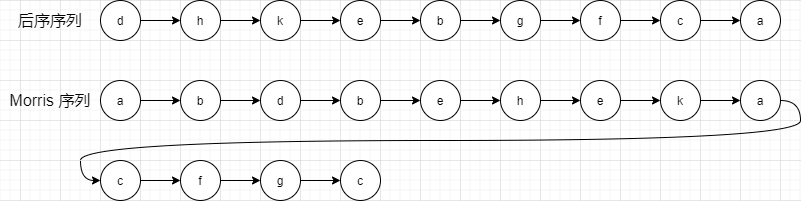
一眼看不出有什么关系
通过 Morris Traversal 得到 后续序列 确实不容易想到,我们直接看前辈们的经验

被遍历到两次的节点的先后顺序:b、e、a、c
1、b 节点的左子树的右边界:d,逆序打印它还是 d
2、e 节点的左子树的右边界:h,逆序打印它还是 h
3、a 节点的左子树的右边界:b -> e -> k,逆序打印就是:k -> e -> b
4、c 节点的左子树的右边界:f -> g,逆序打印就是:g -> f
5、整棵树的右边界:a -> c,逆序打印就是:c -> a
把逆序列串起来:d -> h -> k -> e -> b -> g -> f -> c -> a,这就是 后序序列
问题又来了,如何逆序打印右边界,并且额外空间复杂度 O(1) ;其实就是单向链表的逆序输出,不知道的可以查看:单向链表的花式玩法 → 还在玩反转?
我们来看代码

总结
额外空间复杂度
只用到了有限几个变量, Morris Traversal 额外空间复杂度 O(1)
时间复杂度
Morris Traversal 时间复杂度是不是 O(N) ?
我们先看个极端的案例
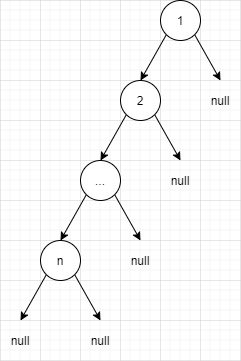
它的时间复杂度是 2 * O(N),这个没什么问题吧?
常数项可以拿掉,所以时间复杂度是 O(N)
注意点
Morris Traversal 遍历过程中会改变二叉树的结构,在一些并发的场景需要慎重使用
参考
《程序员代码面试指南:IT 名企算法与数据结构题目最优解》
额外空间复杂度O(1) 的二叉树遍历 → Morris Traversal,你造吗?的更多相关文章
- 二叉树遍历 Morris
二叉树的遍历,先根遍历,不适用递归,存储空间为 O(1) 转自:http://chuansongme.com/n/100461 MorrisInOrder(): while 没有结束 如果当前节点没有 ...
- 二叉树中序遍历,先序遍历,后序遍历(递归栈,非递归栈,Morris Traversal)
例题 中序遍历94. Binary Tree Inorder Traversal 先序遍历144. Binary Tree Preorder Traversal 后序遍历145. Binary Tre ...
- 二叉树遍历之三(Moriis traversal)
二叉树的Morris traversal是个很值得学习的算法,也是此系列重点想要记叙的一个算法.Morris traversal的一个亮点在于它是O(1)空间复杂度的.前面的递归和迭代都是需要O(n ...
- 二叉树的遍历——Morris
在之前的博客中,博主讨论过二叉树的经典遍历算法,包括递归和常规非递归算法,其时间复杂度和空间复杂度均为O(n).Morris算法巧妙地利用了二叉树的线索化思路,将二叉树的遍历算法的空间复杂度降低为O( ...
- [转载]Morris Traversal方法遍历二叉树(非递归,不用栈,O(1)空间)
本文主要解决一个问题,如何实现二叉树的前中后序遍历,有两个要求: 1. O(1)空间复杂度,即只能使用常数空间: 2. 二叉树的形状不能被破坏(中间过程允许改变其形状). 通常,实现二叉树的前序(pr ...
- 二叉树遍历,递归,栈,Morris
一篇质量非常高的关于二叉树遍历的帖子,转帖自http://noalgo.info/832.html 二叉树遍历(递归.非递归.Morris遍历) 2015年01月06日 | 分类:数据结构 | 标 ...
- Morris Traversal方法遍历二叉树(非递归,不用栈,O(1)空间)——无非是在传统遍历过程中修改叶子结点加入后继结点信息(传统是stack记录),然后再删除恢复
先看看线索二叉树 n个结点的二叉链表中含有n+1(2n-(n-1)=n+1)个空指针域.利用二叉链表中的空指针域,存放指向结点在某种遍历次序下的前驱和后继结点的指针(这种附加的指针称为"线索 ...
- 面试中很值得聊的二叉树遍历方法——Morris遍历
Morri遍历 通过利用空闲指针的方式,来节省空间.时间复杂度O(N),额外空间复杂度O(1).普通的非递归和递归方法的额外空间和树的高度有关,递归的过程涉及到系统压栈,非递归需要自己申请栈空间,都具 ...
- 【数据结构与算法】二叉树的 Morris 遍历(前序、中序、后序)
前置说明 不了解二叉树非递归遍历的可以看我之前的文章[数据结构与算法]二叉树模板及例题 Morris 遍历 概述 Morris 遍历是一种遍历二叉树的方式,并且时间复杂度O(N),额外空间复杂度O(1 ...
随机推荐
- 选择…Select…(Power Query 之 M 语言)
选择行: 筛选Table.SelectRows-文本与数值 筛选Table.SelectRows-日期与时间 保留错误行:= Table.SelectRowsWithErrors( 表, {" ...
- 通过一道简单的例题了解Linux内核PWN
写在前面 这篇文章目的在于简单介绍内核PWN题,揭开内核的神秘面纱.背后的知识点包含Linux驱动和内核源码,学习路线非常陡峭.也就是说,会一道Linux内核PWN需要非常多的铺垫知识,如果要学习可以 ...
- Vim使用简介
Vim操作 Vim真的很酷:D 编辑模式 正常模式:在文件中四处移动光标进行修改 插入模式:插入文本 替换模式:替换文本 可视化(一般,行,块)模式:选中文本块 命令模式:用于执行命令 在不同的操作模 ...
- JAVA遍历某个文件夹下所有文件listFiles() 实现按照名称升序排序
File[] files = file.listFiles(); List fileList = Arrays.asList(files); Collections.sort(fileList, ne ...
- Python obj与JSON相互转换
1 # _*_ coding:utf-8 _*_ 2 3 def showJson(self, pipefd): 4 overdict = args.__dict__ 5 # 此时就可以用json.d ...
- 【LeetCode】453. Minimum Moves to Equal Array Elements 解题报告(Java & Python & C++)
作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 目录 题目描述 题目大意 解题方法 方法一:模拟过程 方法二:求和-n*最小值 方法三: ...
- 【九度OJ】题目1467:二叉排序树 解题报告
[九度OJ]题目1467:二叉排序树 解题报告 标签(空格分隔): 九度OJ http://ac.jobdu.com/problem.php?pid=1467 题目描述: 二叉排序树,也称为二叉查找树 ...
- 【LeetCode】593. Valid Square 解题报告(Python)
[LeetCode]593. Valid Square 解题报告(Python) 作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 题目地 ...
- 晴天小猪历险记之Hill(Dijkstra优先队列优化)
描述 这一天,他来到了一座深山的山脚下,因为只有这座深山中的一位隐者才知道这种药草的所在.但是上山的路错综复杂,由于小小猪的病情,晴天小猪想找一条需时最少的路到达山顶,但现在它一头雾水,所以向你求助. ...
- [平台建设] HBase平台建设实践
背景 由于公司业务场景的需要,我们需要开发HBase平台,主要需要以下功能: 建表管理 授权管理 SDK实现 与公司内部系统打通 我们使用的HBase 版本: HBase 1.2.0-cdh5.16. ...
