图解最长回文子串「Manacher 算法」，基础思路感性上的解析

问题描述：

给你一个字符串 s，找到 s 中最长的回文子串。

链接：https://leetcode-cn.com/problems/longest-palindromic-substring

「Manacher 算法」的整体思路是：基于回文字符串的对称性，缓存前面字符的「臂长」信息，以便后面复用。

这里只以手绘小图片的方式简单讲解「Manacher 算法」

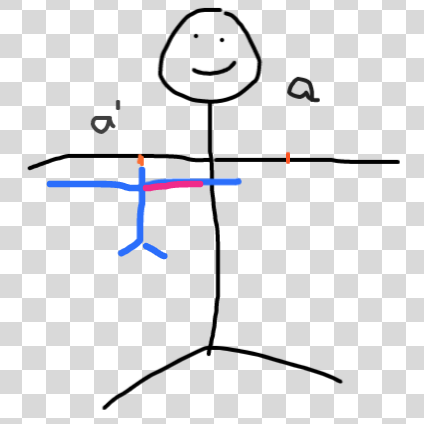
首先设想一个回文字符串，看下图

这个小人以身体为轴，左右对称，可以看作一个回文字符串（设想所有字符分布在其手臂和脖子上）。也就是以脖子为中心，左右对称。

脖子上的字符对应的臂长就是当前手臂的长度。

现在小人的左臂上有一个字符 a

思考如何利用回文串的对称性，快速得出 a 的最小臂长，也就是当 a 为脖子时，它的手臂至少是多长。

.......... 思考中 .........

如果已知右臂上所有字符的臂长，那么可以快速找到 a 的对称点 a'

a' 的臂长跟 a 的臂长之间的关系是什么？

在此图中的情况下，a 的臂长至少至少等于 a' 的臂长。只需要在这个臂长的基础上计算其臂长是否更大。

计算方法就是不断让自己的手臂延长，检查变成之后左右两手是否还相等

如果 a' 的臂长超过了原来的脖子呢

这个情况下，a 的基础臂长是 a' 到脖子的距离

其它边界情况请自行思考

图片是在 https://sketch.io/sketchpad/ 随手画的