Codeforces 986D - Perfect Encoding（FFT+爪巴卡常题）
题意：给出 \(n\)，构造出序列 \(b_1,b_2,\dots,b_m\) 使得 \(\prod\limits_{i=1}^mb_i\geq n\)，求 \(\sum\limits_{i=1}^mb_i\) 的最小值。\(\lg n\leq 1.5\times 10^6\)
被 hb 叫来写这题的题解
u1s1 这题实在是太恐怖了，以下是我的全部非 AC 提交：
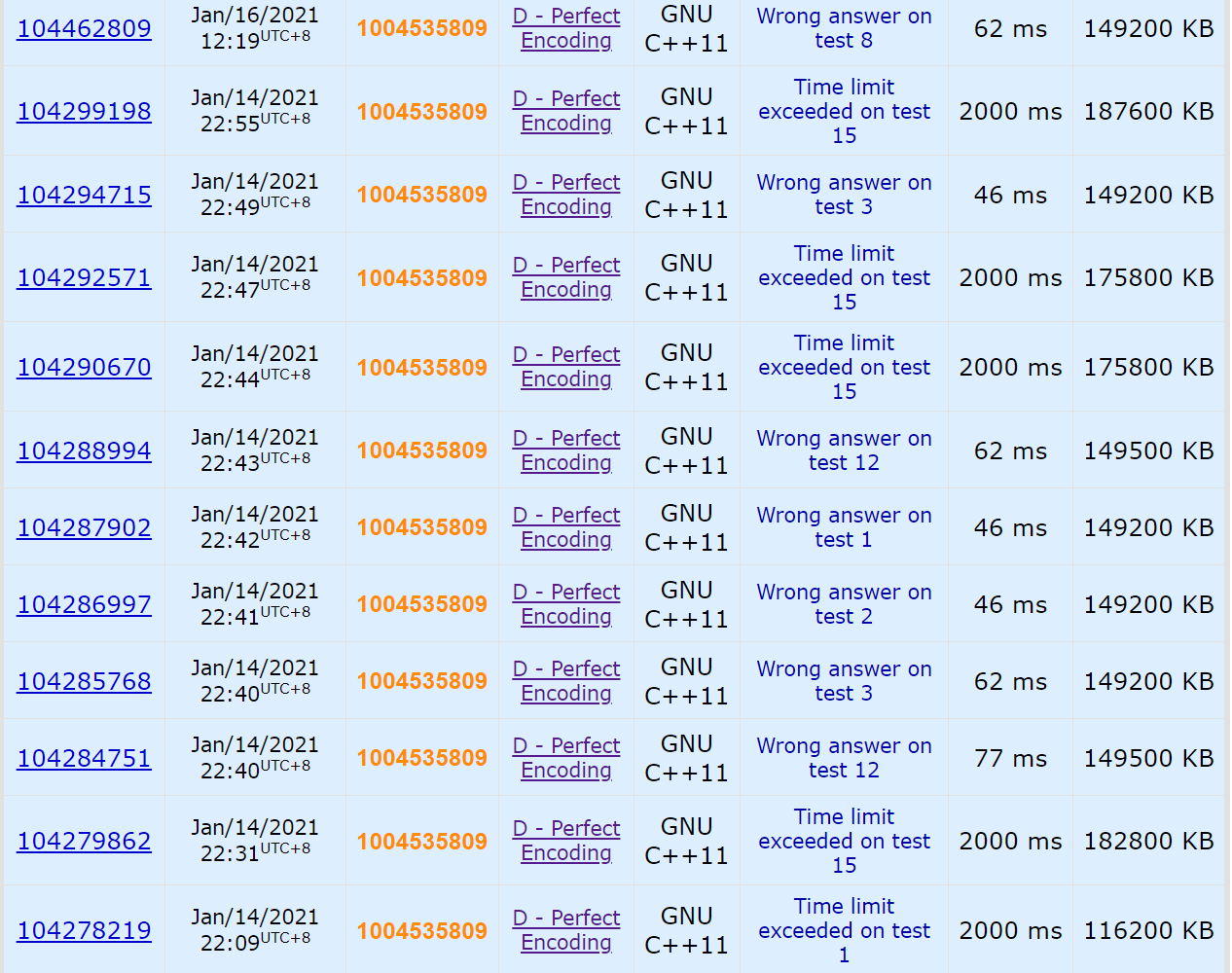
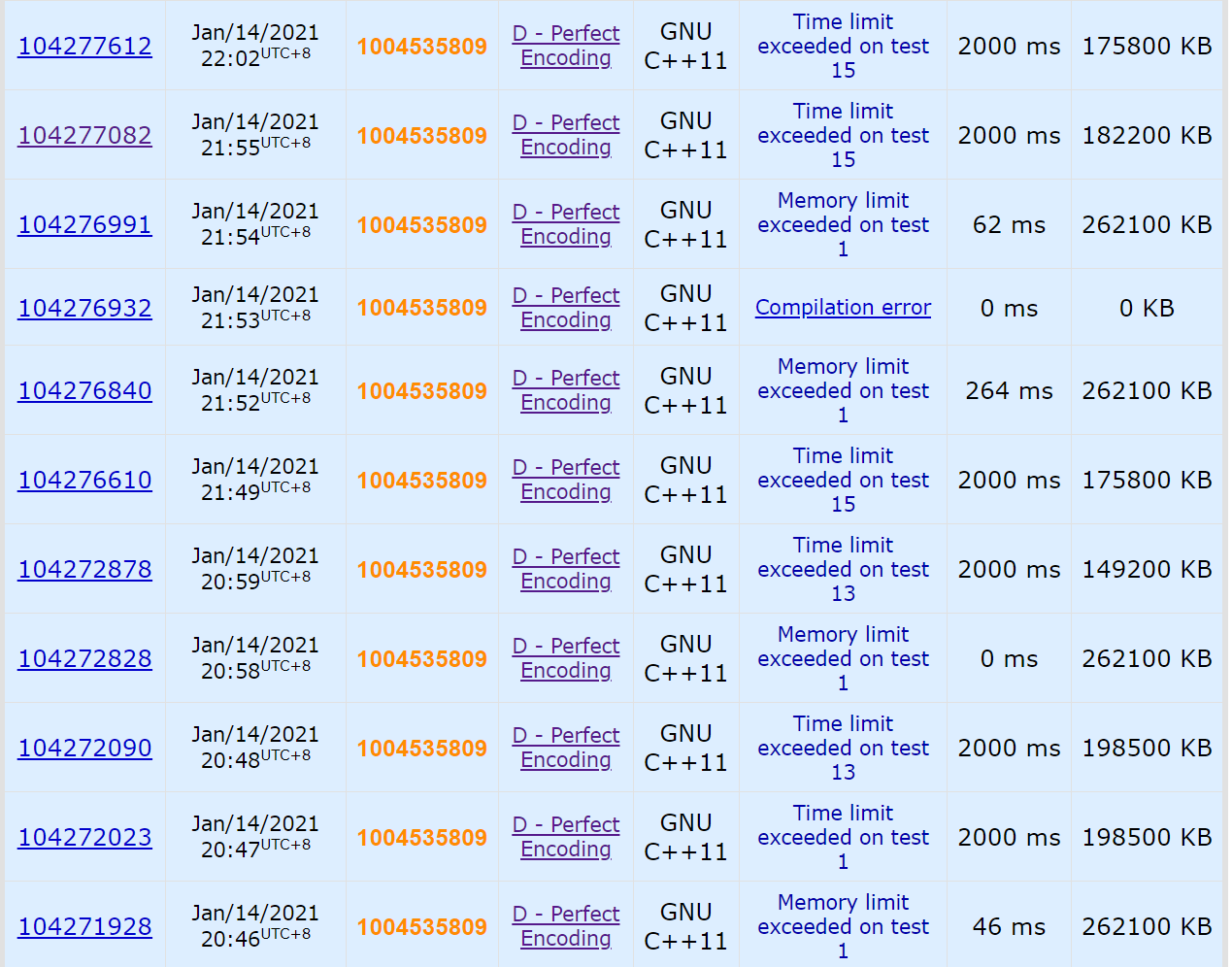
首先直接做肯定是不太容易的。
容易发现答案具有单调性，故可以二分答案，本题转化为一个判定性问题。
我们要求：和为 \(k\) 的若干个数的最大乘积 \(f(k)\) 是多少。
稍微手玩几个数就能发现，最优方案是拆出先若干个 \(3\)，后面零头部分根据 \(k\) 模 \(3\) 的情况拆 \(0\) 或 \(1\) 或 \(2\) 个 \(2\)。
具体来说：
- \(f(k)=3^{k/3}(k\equiv 0\pmod{3})\)
- \(f(k)=2\times 3^{(k-2)/3}(k\equiv 1\pmod{3})\)
- \(f(k)=4\times 3^{(k-4)/3}(k\equiv 2\pmod{3})\)
故我们只需计算出 \(f(k)\) 的值，与 \(n\) 相比较就行了。
注意到本题 \(\lg n\) 是 \(10^6\) 级别的，所以高精乘法要用 FFT 优化。
然后就到了愉快的卡常时间了，这题卡常的经历可谓是一波三折啊：
首先如果你直接上个二分，那么二分中 FFT 复杂度为 \(n\log n\)，外面二分还有个 \(\log\)，你就得到了 \(n\log^2n\) 的优秀复杂度，那肯定是必 T 无疑了。
考虑一个优化方案：注意到答案在 \(3\times\log_3n\) 附近，所以从 \(3\times\log_3n\) 开始暴力枚举答案。我试了一下，这样枚举次数大约在 \(6\) 次附近，这样复杂度就降了一个 \(\log\)。
但仅仅做这一个优化是远远不够的。我最一开始码了个定长的 FFT，也就是每次 FFT 的长度都是 \(> \lg n\) 的最小 \(2\) 的整数次幂，但显然这样没有必要。事实也的确如此，这个程序在 #13 就 TLE 了。
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int MAXN=1.5e6;
const int MAXP=1<<22;
const double LOG310=log(10)/log(3);
const double Pi=acos(-1);
int n,LEN=1,LOG=0;
struct comp{
double x,y;//(real,imag)
comp(){x=y=0;}
comp(double _x,double _y){x=_x;y=_y;}
friend comp operator +(comp lhs,comp rhs){return comp(lhs.x+rhs.x,lhs.y+rhs.y);}
friend comp operator -(comp lhs,comp rhs){return comp(lhs.x-rhs.x,lhs.y-rhs.y);}
friend comp operator *(comp lhs,comp rhs){return comp(lhs.x*rhs.x-lhs.y*rhs.y,lhs.x*rhs.y+lhs.y*rhs.x);}
} A[MAXP+5],B[MAXP+5];
char s[MAXN+5];int x[MAXP+5];
int rev[MAXP+5];
void FFT(comp *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
comp W=comp(cos(2*Pi/i),type*sin(2*Pi/i));
for(int j=0;j<len;j+=i){
comp w=comp(1,0);
for(int k=0;k<(i>>1);k++,w=w*W){
comp X=a[j+k],Y=a[(i>>1)+j+k]*w;
a[j+k]=X+Y;a[(i>>1)+j+k]=X-Y;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i].x=(int)(a[i].x/len+0.5);
}
void polymul(int *a,int *b,int *c){
for(int i=0;i<LEN;i++) A[i]=comp(a[i],0),B[i]=comp(b[i],0);
FFT(A,LEN,1);FFT(B,LEN,1);for(int i=0;i<LEN;i++) A[i]=A[i]*B[i];FFT(A,LEN,-1);
for(int i=0;i<LEN;i++) c[i]=0;
for(int i=0;i<LEN+10;i++){
c[i]+=(int)A[i].x;
if(c[i]>=10) c[i+1]+=c[i]/10,c[i]%=10;
}
}
int a[MAXP+15],b[MAXP+15];
void ksm3(int k){
for(int i=0;i<LEN;i++) a[i]=b[i]=0;
a[0]=1;b[0]=3;
for(;k;k>>=1,polymul(b,b,b)) if(k&1) polymul(a,b,a);
// for(int i=LEN;~i;i--) printf("%d",a[i]);printf("\n");
}
void mul2(int *a){
for(int i=0;i<LEN;i++) a[i]<<=1;
for(int i=0;i<LEN;i++) if(a[i]>=10) a[i]-=10,a[i+1]++;
}
bool check(int mid){
if(mid==0) return 0;
if(mid==1){return (n==1&&s[1]=='1');}
int m2=0;
if(mid%3==1) m2=2,mid-=4;
if(mid%3==2) m2=1,mid-=2;
ksm3(mid/3);for(int i=1;i<=m2;i++) mul2(a);
// for(int i=LEN;~i;i--) printf("%d",a[i]);printf("\n");
for(int i=LEN;~i;i--){
if(a[i]<x[i]) return 0;
if(a[i]>x[i]) return 1;
} return 1;
}
int main(){
scanf("%s",s+1);n=strlen(s+1);
for(int i=0;i<n;i++) x[i]=s[n-i]^48;
int mn=(int)(3.0*LOG310*(n-1));
while(LEN<=n+n) LEN<<=1,LOG++;
// printf("%d\n",mn);
for(int i=mn;;i++) if(check(i)){printf("%d\n",i);return 0;}
return 0;
}
于是我改用 vector 存储大数，在求两个大数 \(a,b\) 的乘积的时候，FFT 的长度取 \(>\lg a+\lg b\) 的最小 \(2\) 的整数次幂，这样可以省去不少无用的操作。
经过这个小小的改动，#13 倒是跑过去了，但 #15 又 T 了。
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int MAXN=1.5e6;
const int MAXP=1<<22;
const double LOG310=log(10)/log(3);
const double Pi=acos(-1);
int n,LEN=1,LOG=0;
struct comp{
double x,y;//(real,imag)
comp(){x=y=0;}
comp(double _x,double _y){x=_x;y=_y;}
friend comp operator +(comp lhs,comp rhs){return comp(lhs.x+rhs.x,lhs.y+rhs.y);}
friend comp operator -(comp lhs,comp rhs){return comp(lhs.x-rhs.x,lhs.y-rhs.y);}
friend comp operator *(comp lhs,comp rhs){return comp(lhs.x*rhs.x-lhs.y*rhs.y,lhs.x*rhs.y+lhs.y*rhs.x);}
} A[MAXP+5],B[MAXP+5];
char s[MAXN+5];vector<int> x;
int rev[MAXP+5];
void FFT(comp *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
comp W=comp(cos(2*Pi/i),type*sin(2*Pi/i));
for(int j=0;j<len;j+=i){
comp w=comp(1,0);
for(int k=0;k<(i>>1);k++,w=w*W){
comp X=a[j+k],Y=a[(i>>1)+j+k]*w;
a[j+k]=X+Y;a[(i>>1)+j+k]=X-Y;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i].x=(int)(a[i].x/len+0.5);
}
vector<int> polymul(vector<int> a,vector<int> b){
int len=1;
while(len<=a.size()+b.size()) len<<=1;
for(int i=0;i<len;i++) A[i]=B[i]=comp(0,0);
for(int i=0;i<a.size();i++) A[i]=comp(a[i],0);
for(int i=0;i<b.size();i++) B[i]=comp(b[i],0);
FFT(A,len,1);FFT(B,len,1);
for(int i=0;i<len;i++) A[i]=A[i]*B[i];
FFT(A,len,-1);
vector<int> c(a.size()+b.size(),0);
for(int i=0;i<c.size();i++){
c[i]+=(int)A[i].x;
if(c[i]>=10) c[i+1]+=c[i]/10,c[i]%=10;
} if(c.back()==0) c.pop_back();
return c;
}
vector<int> ksm3(int k){
vector<int> a,b;a.pb(1);b.pb(3);
for(;k;k>>=1,b=polymul(b,b)) if(k&1) a=polymul(a,b);
// for(int i=LEN;~i;i--) printf("%d",a[i]);printf("\n");
return a;
}
vector<int> mul2(vector<int> a){
for(int i=0;i<a.size();i++) a[i]<<=1;
for(int i=0;i<(int)(a.size()-1);i++) if(a[i]>=10) a[i]-=10,a[i+1]++;
if(a[a.size()-1]>=10) a[a.size()-1]-=10,a.pb(1);
return a;
}
bool check(int mid){
if(mid==0) return 0;
if(mid==1){return (n==1&&s[1]=='1');}
int m2=0;
if(mid%3==1) m2=2,mid-=4;
if(mid%3==2) m2=1,mid-=2;
vector<int> a=ksm3(mid/3);for(int i=1;i<=m2;i++) a=mul2(a);
// for(int i=(int)(a.size()-1);~i;i--) printf("%d",a[i]);printf("\n");
if(a.size()<x.size()) return 0;
if(a.size()>x.size()) return 1;
for(int i=(int)(a.size()-1);~i;i--){
if(a[i]<x[i]) return 0;
if(a[i]>x[i]) return 1;
} return 1;
}
int main(){
scanf("%s",s+1);n=strlen(s+1);
for(int i=n;i;i--) x.pb(s[i]^48);
int mn=(int)(3.0*LOG310*(n-1));
// printf("%d\n",mn);
for(int i=mn;;i++) if(check(i)){printf("%d\n",i);return 0;}
return 0;
}
继续卡，在快速幂过程中，我们要对 \(x\) 进行自乘。在这种情况下并不用做 2 次 DFT+1 次 IDFT，可以 1 次 DFT+1 次 IDFT 搞定（事实上，普通的多项式乘法 1 次 DFT+1 次 IDFT 也可以搞定，不过我还不会），有一定效果，不过还是没能摆脱 TLE 的命运。
很明显，每次求 \(f(k)\) 的过程中指数上那个东西相差都不太大，都在 \(\log_3n\) 左右，这意味着你并不用每次求 \(f(k)\) 都跑一遍快速幂，可以在枚举答案前先预处理 \(p=3^{\lfloor\log_3n\rfloor}\)，每次求 \(f(k)\) 都在 \(p\) 的基础上乘几个 \(3\) 或乘几个 \(2\)。一个长度为 \(n\) 的大数乘一个一位数是 \(\mathcal O(n)\) 级别的，于是每次求 \(f(k)\) 的复杂度也降了下来，达到了 \(\mathcal O(\lg n)\) 。
跑得快了亿点点，#14 从原来 717ms 降到了 140ms。不过手造了组 \(1.5\times 10^6\) 的数据本地跑了 4s。
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int MAXN=1.5e6;
const int MAXP=1<<22;
const double LOG310=log(10)/log(3);
const double Pi=acos(-1);
int n,LEN=1,LOG=0;
struct comp{
double x,y;//(real,imag)
comp(){x=y=0;}
comp(double _x,double _y){x=_x;y=_y;}
friend comp operator +(comp lhs,comp rhs){return comp(lhs.x+rhs.x,lhs.y+rhs.y);}
friend comp operator -(comp lhs,comp rhs){return comp(lhs.x-rhs.x,lhs.y-rhs.y);}
friend comp operator *(comp lhs,comp rhs){return comp(lhs.x*rhs.x-lhs.y*rhs.y,lhs.x*rhs.y+lhs.y*rhs.x);}
} A[MAXP+5],B[MAXP+5];
char s[MAXN+5];vector<int> x;
int rev[MAXP+5];
vector<int> pp;int lv;
void FFT(comp *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
comp W=comp(cos(2*Pi/i),type*sin(2*Pi/i));
for(int j=0;j<len;j+=i){
comp w=comp(1,0);
for(int k=0;k<(i>>1);k++,w=w*W){
comp X=a[j+k],Y=a[(i>>1)+j+k]*w;
a[j+k]=X+Y;a[(i>>1)+j+k]=X-Y;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i].x=(int)(a[i].x/len+0.5);
}
vector<int> polymul(vector<int> a,vector<int> b){
int len=1;
while(len<=a.size()+b.size()) len<<=1;
if(len>MAXP) return a;
for(int i=0;i<len;i++) A[i]=B[i]=comp(0,0);
for(int i=0;i<a.size();i++) A[i]=comp(a[i],0);
for(int i=0;i<b.size();i++) B[i]=comp(b[i],0);
FFT(A,len,1);FFT(B,len,1);
for(int i=0;i<len;i++) A[i]=A[i]*B[i];
FFT(A,len,-1);
vector<int> c(a.size()+b.size(),0);
for(int i=0;i<c.size();i++){
c[i]+=(int)A[i].x;
if(c[i]>=10) c[i+1]+=c[i]/10,c[i]%=10;
} if(c.back()==0) c.pop_back();
return c;
}
vector<int> ksm3(int k){
vector<int> a,b;a.pb(1);b.pb(3);
for(;k;k>>=1,b=polymul(b,b)) if(k&1) a=polymul(a,b);
// for(int i=LEN;~i;i--) printf("%d",a[i]);printf("\n");
return a;
}
vector<int> mul(vector<int> a,int t){
for(int i=0;i<a.size();i++) a[i]*=t;
for(int i=0;i<(int)(a.size()-1);i++) if(a[i]>=10) a[i+1]+=a[i]/10,a[i]%=10;
if(a[a.size()-1]>=10) a.pb(a[a.size()-1]/10),a[a.size()-2]%=10;
return a;
}
bool check(int mid){
if(mid==0) return 0;
if(mid==1){return (n==1&&s[1]=='1');}
int m2=0;
if(mid%3==1) m2=2,mid-=4;
if(mid%3==2) m2=1,mid-=2;
vector<int> a=pp;
for(int i=1;i<=mid/3-lv;i++) a=mul(a,3);
for(int i=1;i<=m2;i++) a=mul(a,2);
// for(int i=(int)(a.size()-1);~i;i--) printf("%d",a[i]);printf("\n");
if(a.size()<x.size()) return 0;
if(a.size()>x.size()) return 1;
for(int i=(int)(a.size()-1);~i;i--){
if(a[i]<x[i]) return 0;
if(a[i]>x[i]) return 1;
} return 1;
}
int main(){
// freopen("in.txt","r",stdin);
scanf("%s",s+1);n=strlen(s+1);
for(int i=n;i;i--) x.pb(s[i]^48);
int mn=(int)(3.0*LOG310*(n-1));
lv=max(mn/3-3,0);pp=ksm3(lv);
// printf("%d\n",mn);
for(int i=mn;;i++) if(check(i)){printf("%d\n",i);return 0;}
return 0;
}
于是我开始搜各种 FFT 卡常技巧，感觉博客里所谓的“卡常技巧”，大多数都没啥用，唯独一条感觉有点用，那就是：
comp operator +(const comp rhs){return comp(x+rhs.x,y+rhs.y);}
在参数里面加个传引用：
comp operator +(const comp &rhs){return comp(x+rhs.x,y+rhs.y);}
原因未知，不过的确快了一点点，140ms 变成了 109ms，手造的数据也变成了 3.3s。
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int MAXN=1.5e6;
const int MAXP=1<<22;
const double LOG310=log(10)/log(3);
const double Pi=acos(-1);
int n,LEN=1,LOG=0;
struct comp{
double x,y;//(real,imag)
comp(){x=y=0;}
comp(double _x,double _y){x=_x;y=_y;}
comp operator +(const comp &rhs){return comp(x+rhs.x,y+rhs.y);}
comp operator -(const comp &rhs){return comp(x-rhs.x,y-rhs.y);}
comp operator *(const comp &rhs){return comp(x*rhs.x-y*rhs.y,x*rhs.y+y*rhs.x);}
} A[MAXP+5],B[MAXP+5];
char s[MAXN+5];vector<int> x;
int rev[MAXP+5];
vector<int> pp;int lv;
void FFT(comp *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
comp W=comp(cos(2*Pi/i),type*sin(2*Pi/i));
for(int j=0;j<len;j+=i){
comp w=comp(1,0);
for(int k=0;k<(i>>1);k++,w=w*W){
comp X=a[j+k],Y=a[(i>>1)+j+k]*w;
a[j+k]=X+Y;a[(i>>1)+j+k]=X-Y;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i].x=(int)(a[i].x/len+0.5);
}
vector<int> polymul(vector<int> a,vector<int> b){
int len=1;
while(len<=a.size()+b.size()) len<<=1;
for(int i=0;i<len;i++) A[i]=B[i]=comp(0,0);
for(int i=0;i<a.size();i++) A[i]=comp(a[i],0);
for(int i=0;i<b.size();i++) B[i]=comp(b[i],0);
FFT(A,len,1);FFT(B,len,1);
for(int i=0;i<len;i++) A[i]=A[i]*B[i];
FFT(A,len,-1);
vector<int> c(a.size()+b.size());
for(int i=0;i<c.size();i++){
c[i]+=(int)A[i].x;
if(c[i]>=10) c[i+1]+=c[i]/10,c[i]%=10;
} if(c.back()==0) c.pop_back();
return c;
}
vector<int> ksm3(int k){
vector<int> a,b;a.pb(1);b.pb(3);
for(;k;k>>=1){
if(k&1) a=polymul(a,b);
int len=1;
while(len<=b.size()*2) len<<=1;
if(len>MAXP) break;
for(int i=0;i<len;i++) A[i]=comp(0,0);
for(int i=0;i<b.size();i++) A[i]=comp(b[i],0);
FFT(A,len,1);
for(int i=0;i<len;i++) A[i]=A[i]*A[i];
FFT(A,len,-1);
vector<int> c(b.size()*2,0);
for(int i=0;i<c.size();i++){
c[i]+=(int)A[i].x;
if(c[i]>=10) c[i+1]+=c[i]/10,c[i]%=10;
} if(c.back()==0) c.pop_back();b=c;
}
// for(int i=LEN;~i;i--) printf("%d",a[i]);printf("\n");
return a;
}
vector<int> mul(vector<int> a,int t){
for(int i=0;i<a.size();i++) a[i]*=t;
for(int i=0;i<(int)(a.size()-1);i++) if(a[i]>=10) a[i+1]+=a[i]/10,a[i]%=10;
if(a[a.size()-1]>=10) a.pb(a[a.size()-1]/10),a[a.size()-2]%=10;
return a;
}
bool check(int mid){
if(mid==0) return 0;
if(mid==1){return (n==1&&s[1]=='1');}
int m2=0;
if(mid%3==1) m2=2,mid-=4;
if(mid%3==2) m2=1,mid-=2;
vector<int> a=pp;
for(int i=1;i<=mid/3-lv;i++) a=mul(a,3);
for(int i=1;i<=m2;i++) a=mul(a,2);
// for(int i=(int)(a.size()-1);~i;i--) printf("%d",a[i]);printf("\n");
if(a.size()<x.size()) return 0;
if(a.size()>x.size()) return 1;
for(int i=(int)(a.size()-1);~i;i--){
if(a[i]<x[i]) return 0;
if(a[i]>x[i]) return 1;
} return 1;
}
int main(){
// freopen("in.txt","r",stdin);
scanf("%s",s+1);n=strlen(s+1);
for(int i=n;i;i--) x.pb(s[i]^48);
int mn=(int)(3.0*LOG310*(n-1));
lv=max(mn/3-2,0);pp=ksm3(lv);
// printf("%d\n",mn);
for(int i=mn;;i++) if(check(i)){printf("%d\n",i);return 0;}
return 0;
}
感觉没什么地方可卡了。然后就彻底自闭了，开始绞劲脑汁想如何进一步卡常。想了好久终于想出了一种方法，那就是对高精进行压位，两位压成一位，这样 FFT 的时候数组长度可以减少一半，常数也变成原来的一半了。
经过这样的改动，极限数据由 3.3s 变成了 2s，也就 AC 了这道题。
大功告成。
最后是 AC 代码：
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
x=0;char c=getchar();T neg=1;
while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
while(isdigit(c)) x=x*10+c-'0',c=getchar();
x*=neg;
}
const int MAXN=1.5e6;
const int MAXP=1<<21;
const int WIDTH=100;
const double LOG310=log(10)/log(3);
const double Pi=acos(-1);
int n,LEN=1,LOG=0;
struct comp{
double x,y;//(real,imag)
comp(){x=y=0;}
comp(double _x,double _y){x=_x;y=_y;}
comp operator +(const comp &rhs){return comp(x+rhs.x,y+rhs.y);}
comp operator -(const comp &rhs){return comp(x-rhs.x,y-rhs.y);}
comp operator *(const comp &rhs){return comp(x*rhs.x-y*rhs.y,x*rhs.y+y*rhs.x);}
} A[MAXP+5],B[MAXP+5];
char s[MAXN+5];vector<int> x;
int rev[MAXP+5];
vector<int> pp;int lv;
void FFT(comp *a,int len,int type){
int lg=log2(len);
for(int i=0;i<len;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
for(int i=2;i<=len;i<<=1){
comp W=comp(cos(2*Pi/i),type*sin(2*Pi/i));
for(int j=0;j<len;j+=i){
comp w=comp(1,0);
for(int k=0;k<(i>>1);k++,w=w*W){
comp X=a[j+k],Y=a[(i>>1)+j+k]*w;
a[j+k]=X+Y;a[(i>>1)+j+k]=X-Y;
}
}
}
if(type==-1) for(int i=0;i<len;i++) a[i].x=(int)(a[i].x/len+0.5);
}
vector<int> polymul(vector<int> a,vector<int> b){
int len=1;
while(len<=a.size()+b.size()) len<<=1;
for(int i=0;i<len;i++) A[i]=B[i]=comp(0,0);
for(int i=0;i<a.size();i++) A[i]=comp(a[i],0);
for(int i=0;i<b.size();i++) B[i]=comp(b[i],0);
FFT(A,len,1);FFT(B,len,1);
for(int i=0;i<len;i++) A[i]=A[i]*B[i];
FFT(A,len,-1);
vector<int> c(a.size()+b.size());
for(int i=0;i<c.size();i++){
c[i]+=(int)A[i].x;
if(c[i]>=WIDTH) c[i+1]+=c[i]/WIDTH,c[i]%=WIDTH;
} if(c.back()==0) c.pop_back();
return c;
}
vector<int> ksm3(int k){
vector<int> a,b;a.pb(1);b.pb(3);
for(;k;k>>=1){
if(k&1) a=polymul(a,b);
int len=1;
while(len<=b.size()*2) len<<=1;
if(len>MAXP) break;
for(int i=0;i<len;i++) A[i]=comp(0,0);
for(int i=0;i<b.size();i++) A[i]=comp(b[i],0);
FFT(A,len,1);
for(int i=0;i<len;i++) A[i]=A[i]*A[i];
FFT(A,len,-1);
vector<int> c(b.size()*2,0);
for(int i=0;i<c.size();i++){
c[i]+=(int)A[i].x;
if(c[i]>=WIDTH) c[i+1]+=c[i]/WIDTH,c[i]%=WIDTH;
} if(c.back()==0) c.pop_back();b=c;
}
// for(int i=LEN;~i;i--) printf("%d",a[i]);printf("\n");
return a;
}
vector<int> mul(vector<int> a,int t){
for(int i=0;i<a.size();i++) a[i]*=t;
for(int i=0;i<(int)(a.size()-1);i++) if(a[i]>=WIDTH) a[i+1]+=a[i]/WIDTH,a[i]%=WIDTH;
if(a[a.size()-1]>=WIDTH) a.pb(a[a.size()-1]/WIDTH),a[a.size()-2]%=WIDTH;
return a;
}
bool check(int mid){
if(mid==0) return 0;
if(mid==1){return (n==1&&s[1]=='1');}
int m2=0;
if(mid%3==1) m2=2,mid-=4;
if(mid%3==2) m2=1,mid-=2;
vector<int> a=pp;
for(int i=1;i<=mid/3-lv;i++) a=mul(a,3);
for(int i=1;i<=m2;i++) a=mul(a,2);
vector<int> b;
for(int i=0;i<a.size();i++){b.pb(a[i]%10);b.pb(a[i]/10);}
if(b.back()==0) b.pop_back();
// for(int i=(int)(a.size()-1);~i;i--) printf("%d",a[i]);printf("\n");
if(b.size()<x.size()) return 0;
if(b.size()>x.size()) return 1;
for(int i=(int)(b.size()-1);~i;i--){
if(b[i]<x[i]) return 0;
if(b[i]>x[i]) return 1;
} return 1;
}
int main(){
// freopen("in.txt","r",stdin);
scanf("%s",s+1);n=strlen(s+1);
for(int i=n;i;i--) x.pb(s[i]^48);
int mn=(int)(3.0*LOG310*(n-1));
lv=max(mn/3-2,0);pp=ksm3(lv);
// printf("%d\n",mn);
for(int i=mn;;i++) if(check(i)){printf("%d\n",i);return 0;}
return 0;
}
你可能会说，NTT 不是比 FFT 快吗？如果改成 NTT 会怎么样呢？
那我要告诉你：不开 O2 NTT 比 FFT 快，开 O2 FFT 比 NTT 快
翻了下前几名的代码，发现他们也都是用 vector 存储大数，并预处理 \(p=3^{\lfloor\log_3n\rfloor}\)，然后从 \(3\log_3n\) 处暴力枚举答案的。除此之外，他们还用了一些别的卡常技巧，如 tourist 用了 1 次 DFT+1 次 IDFT的多项式乘法，dyh 也在参数里面加了个传引用，LHiC 也是在自乘那个地方手写了一个函数 mult2 等等，这一类的卡常技巧在碰到 dl 卡常题的时候也都是能派上用场的。
话说这场的 E 我是不是做过啊，当年我也卡了一天的常来着的？
Codeforces 986D - Perfect Encoding（FFT+爪巴卡常题）的更多相关文章
- Codeforces 986D Perfect Encoding FFT 分治 高精度
原文链接https://www.cnblogs.com/zhouzhendong/p/9161557.html 题目传送门 - Codeforces 986D 题意 给定一个数 $n(n\leq 10 ...
- Codeforces 986D Perfect Encoding FFT
题意: 给定一个数n,选出m个数使得 $\Pi_{i=1}^m a_i\ge n$,求$\sum_{i=1}^m a_i$的最小值 ,其中$m$的大小不限 $n$的长度$\le 10^6$ 简单的计算 ...
- NOIP模拟测试39,思维禁锢专场「工业题·玄学题·卡常题」
工业题 题解 抱歉,题解没时间写了 代码 #include<bits/stdc++.h> using namespace std; #define ll long long #define ...
- [CSP-S模拟测试]:卡常题/b（基环树+DP）
题目描述 $ρ$有一个二分连通无向图,$X$方点.$Y$方点均为$n$个(编号为$1\sim n$).这个二分图比较特殊,每一个$Y$方点的度为$2$,一条黑色边,一条白色边.所有黑色边权值均为$a$ ...
- BZOJ4836: [Lydsy1704月赛]二元运算【分治FFT】【卡常（没卡过）】
Description 定义二元运算 opt 满足 现在给定一个长为 n 的数列 a 和一个长为 m 的数列 b ,接下来有 q 次询问.每次询问给定一个数字 c 你需要求出有多少对 (i, j) 使 ...
- CodeForces 327E Axis Walking(状压DP+卡常技巧)
Iahub wants to meet his girlfriend Iahubina. They both live in Ox axis (the horizontal axis). Iahub ...
- NOIP 模拟 $13\; \text{卡常题}$
题解 一道环套树的最小点覆盖题目,所谓环套树就是有在 \(n\) 个点 \(n\) 条边的无向联通图中存在一个环 我们可以发现其去掉一条环上的边后就是一棵树 那么对于此题,我们把所有 \(x\) 方点 ...
- NOIP模拟13「工业题·卡常题·玄学题」
T1:工业题 基本思路 这题有一个重要的小转化: 我们将原来的函数看作一个矩阵,\(f(i,j-1)*a\)相当于从\(j-1\)向右走一步并贡献a,\(f(i-1,j)*b\)相当于从\(i-1 ...
- 洛谷 P5046 [Ynoi2019 模拟赛] Yuno loves sqrt technology I（分块+卡常）
洛谷题面传送门 zszz,lxl 出的 DS 都是卡常题( 首先由于此题强制在线,因此考虑分块,我们那么待查询区间 \([l,r]\) 可以很自然地被分为三个部分: 左散块 中间的整块 右散块 那么这 ...
随机推荐
- Golang通脉之数组
数组是同一种数据类型元素的集合.数组在内存中都是连续存放的. 在Go语言中,数组从声明时就确定,使用时可以修改数组成员,但是数组大小不可变化. 基本语法: // 定义一个长度为3元素类型为int的数组 ...
- 最详细的Android SDK下载安装及配置教程-------全文均为引用
<https://www.cnblogs.com/gufengchen/p/11038029.html>
- 【Java虚拟机5】Java内存模型（硬件层面的并发优化基础知识--指令乱序问题）
前言 其实之前大家都了解过volatile,它的第一个作用是保证内存可见,第二个作用是禁止指令重排序.今天系统学习下为什么CPU会指令重排. 存储器的层次结构图 1.CPU乱序执行指令的根源 CPU读 ...
- 防止SQL注入总结
1.预编译(占位符)可以很大程度上防止SQL注入 预编译的原理是数据库厂商提供的JAR包中,对参数进行了转义 2.mybatis中,能用# 的地方,不用$,因为#是预编译占位符形式,可以防止SQL注入 ...
- [对对子队]会议记录4.16(Scrum Meeting7)
今天已完成的工作 何瑞 工作内容:完成成本和分数系统 相关issue:实现成本和分数系统的逻辑 相关签入:4.16签入1 吴昭邦 工作内容:对接流水线和成本和分数系统 相关issu ...
- 【行人惯性导航】关于行人导航中IMU位姿推导的知识点及相关代码
IMU姿态惯性推导 最近从事行人惯性导航的研究,本人也是一个小白,其中看了很多文献,有很多个人思考很费时间的地方,撰写此随笔的目的不仅是给自己做一个笔记,也是给各位有需要的仁兄一点个人理解. 本文只关 ...
- C++实现红黑树
红黑树的应用: 利用key_value对,快速查找,O(logn) socket与客户端id之间,形成映射关系(socket, id) 内存分配管理 一整块内存,不断分配小块 每分配一次,就加入到红黑 ...
- spring-cloud-square源码速读(spring-cloud-square-okhttp篇)
欢迎访问我的GitHub https://github.com/zq2599/blog_demos 内容:所有原创文章分类汇总及配套源码,涉及Java.Docker.Kubernetes.DevOPS ...
- pycharm基本使用python的注释语法
pychram基本使用 1.主题选择 file settings Editor color Scheme 2.pycharm切换解释器 file settings Project Python Int ...
- notepad++ 替换回车换行
以" | "为分隔符,换行 结果如下图: