ACM数论之旅17---反演定理 第一回 二项式反演（神说要有光 于是就有了光(´・ω・`)）

终于讲到反演定理了，反演定理这种东西记一下公式就好了，反正我是证明不出来的~(～o￣▽￣)～o

首先，著名的反演公式

我先简单的写一下o(￣ヘ￣*o)

比如下面这个公式

f(n) = g(1) + g(2) + g(3) + ... + g(n)

如果你知道g(x)，蓝后你就可以知道f(n)了

如果我知道f(x)，我想求g(n)怎么办

这个时候，就有反演定理了

反演定理可以轻松的把上面的公式变为

g(n) = f(1) + f(2) + f(3) + ... + f(n)

当然，我写的只是个形式，怎么可能这么简单｡◕‿◕｡

其实每一项再乘一个未知的函数就对了，但是这个函数我们不知道（不用担心，数学家已经帮我们解决了，我们直接用就可以了）

反演公式登场( ＞ω＜)

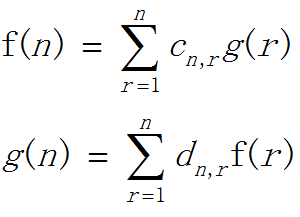
c和d是两个跟n和r有关的函数

根据用法不同，c和d是不同的

一般数学家会先随便弄c函数

然后经过复杂的计算和证明，得到d函数

然后公式就可以套用了

正片开始

二项式反演公式

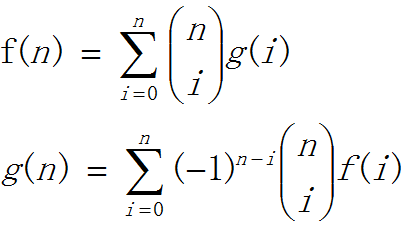
那个括号起来的就是组合数，我记得组合数那章我有说过

二项式反演也就是记住这个公式就算结束了

然后我们开始实战(/ω＼)

容斥那章讲过的全错排（装错信封问题）

hdu 1465

http://acm.hdu.edu.cn/showproblem.php?pid=1465

设g(i)表示正好有i封信装错信封

那么全部的C(n, i)*g(i)加起来正好就是所有装信的情况，总共n!种情况

n! = Σ C(n, i)*g(i) (i从0到n)

那么f(n) = n!，所以f(x) = x!

那么我们要求g(n)

根据公式

g(n) = Σ (-1)^(n-i) * C(n, i) * f(i)  (i从0到n)

那么就可以计算啦~\(≧▽≦)/~

AC代码：

 #include<cstdio>
 typedef long long LL;
 int n, flag;
 LL fac[];
 LL ans;
 void init(){
     fac[] = ;
     for(int i = ; i <= ; i ++) fac[i] = fac[i-] * i;
 }
 int main(){
     init();
     while(~scanf("%d", &n)){
         ans = ;
         flag = n &  ? - : ;//起始符号
         for(int i = ; i <= n; i ++){
             ans += flag * fac[n] / fac[n-i];
             flag = -flag;
         }
         printf("%I64d\n", ans);
     }
 }

是不是很好用但是不容易想到T_T

这也没有办法

再来一题吧

还是容斥那一章讲过的题目的

UVALive 7040

https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=5052

题意：给n盆花涂色，从m种颜色中选取k种颜色涂，保证正好用上k种颜色，你必须用上这k种颜色去涂满n个相邻的花，并且要求相邻花的颜色不同，求方案数。

(1 ≤ n, m ≤ 1e9 , 1 ≤ k ≤ 1e6 , k ≤ n, m)

首先，用k种颜色涂花，假如不考虑全部用上，那么总的方案数是多少

第一盆花有k种颜色选择，之后的花因为不能跟前一盆花的颜色相同，所以有k-1种选择

于是总方案数为k*(k-1)^(n-1)

我们设必须用 i 种颜色两两不相邻的涂花的方案数为 g(i)

那么

k*(k-1)^(n-1) = Σ C(k, i)*g(i) (i从1到k)

令f(k) = k*(k-1)^(n-1)，那么f(x) = x*(x-1)^(n-1)

二项式反演公式出现了

所以g(k) = Σ (-1)^(k-i) * C(k, i) * f(i)  (i从1到k)

最终的答案就是C(m, k) * g(k)

（这里m有1e9，C(m, k)直接用for循环算，直接for循环从m*(m-1)*...*(m-k+1)再乘k的阶乘的逆元）

AC代码：

 #include<cstdio>
 typedef long long LL;
 const int N =  + ;
 const int MOD = (int)1e9 + ;
 int F[N], Finv[N], inv[N];
 LL pow_mod(LL a, LL b, LL p){
     LL ret = ;
     while(b){
         if(b & ) ret = (ret * a) % p;
         a = (a * a) % p;
         b >>= ;
     }
     return ret;
 }
 void init(){
     inv[] = ;
     for(int i = ; i < N; i ++){
         inv[i] = (MOD - MOD / i) * 1ll * inv[MOD % i] % MOD;
     }
     F[] = Finv[] = ;
     for(int i = ; i < N; i ++){
         F[i] = F[i-] * 1ll * i % MOD;
         Finv[i] = Finv[i-] * 1ll * inv[i] % MOD;
     }
 }
 int comb(int n, int m){
     if(m <  || m > n) return ;
     return F[n] * 1ll * Finv[n - m] % MOD * Finv[m] % MOD;
 }
 int main(){
     init();
     int T, n, m, k, ans, flag, temp;
     scanf("%d", &T);
     for(int cas = ; cas <= T; cas ++){
         scanf("%d%d%d", &n, &m, &k);
         ans = ;
         flag = (k & ) ?  : -;
         //计算g(k)
         for(int i = ; i <= k; i ++){
             ans = (ans + 1ll * flag * comb(k, i) * i % MOD * pow_mod(i-, n-, MOD) % MOD) % MOD;
             flag = -flag;
         }
         //接下来计算C(m, k)
         temp = Finv[k];
         for(int i = ; i <= k; i ++){
             temp = 1ll * temp * (m-k+i) % MOD;
         }
         ans = ((1ll * ans * temp) % MOD + MOD) % MOD;
         printf("Case #%d: %d\n", cas, ans);
     }
 }

做完两题之后就感觉二项式反演变得容易了，遇到题目还是要多想(￣▽￣")

等等。。。做完两题的我突然发现二项式反演和容斥推倒出来的公式总是一样的。。。。。。（为什么有种被骗的感觉T_T）