洛谷 P3373：【模板】线段树 2（区间更新）

题目描述

如题，已知一个数列，你需要进行下面三种操作：

1.将某区间每一个数乘上x

2.将某区间每一个数加上x

3.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

输出格式：

输出包含若干行整数，即为所有操作3的结果。

输入输出样例

输入样例#1： 复制

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

输出样例#1： 复制

17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

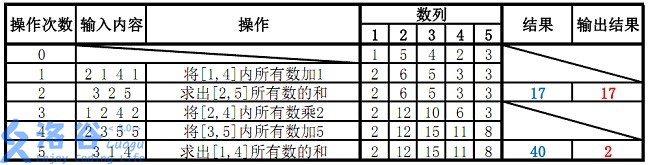
故输出应为17、2（40 mod 38=2）

AC代码

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <math.h>
#include <limits.h>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#include <set>
#include <string>
#define ll long long
#define ull unsigned long long
#define ms(a) memset(a,0,sizeof(a))
#define pi acos(-1.0)
#define INF 0x7f7f7f7f
#define lson o<<1
#define rson o<<1|1
const double E=exp(1);
const ll maxn=1e6+10;
using namespace std;
ll n,m,mod;
struct wzy
{
	ll left,right,len;
	ll value;
	ll lazy;//加法
	ll lazy1;//乘法
}p[maxn];
void push_up(ll o)
{
	p[o].value=(p[lson].value+p[rson].value)%mod;
}
void push_down(ll o)
{
	if(p[o].lazy||p[o].lazy1!=1)
	{
		p[lson].lazy=(p[lson].lazy*p[o].lazy1+p[o].lazy)%mod;
		p[rson].lazy=(p[rson].lazy*p[o].lazy1+p[o].lazy)%mod;
		p[lson].lazy1=(p[o].lazy1*p[lson].lazy1)%mod;
		p[rson].lazy1=(p[o].lazy1*p[rson].lazy1)%mod;
		p[lson].value=(p[lson].value*p[o].lazy1+p[o].lazy*p[lson].len)%mod;
		p[rson].value=(p[rson].value*p[o].lazy1+p[o].lazy*p[rson].len)%mod;
		p[o].lazy=0;
		p[o].lazy1=1;
	}
}
void build(ll o,ll l,ll r)
{
	p[o].left=l;p[o].right=r;
	p[o].len=r-l+1;
	p[o].lazy=0;
	p[o].lazy1=1;
	if(l==r)
	{
		ll x;
		scanf("%lld",&x);
		p[o].value=x;
		return ;
	}
	ll mid=(l+r)>>1;
	build(lson,l,mid);
	build(rson,mid+1,r);
	push_up(o);
}
void update(ll o,ll l,ll r,ll v)//相加
{
	if(p[o].left>=l&&p[o].right<=r)
	{
		p[o].lazy=(p[o].lazy+v)%mod;
		p[o].value=(p[o].value+v*p[o].len)%mod;
		return ;
	}
	push_down(o);
	ll mid=(p[o].left+p[o].right)>>1;
	if(r<=mid)
		update(lson,l,r,v);
	else if(l>mid)
		update(rson,l,r,v);
	else
	{
		update(lson,l,mid,v);
		update(rson,mid+1,r,v);
	}
	push_up(o);
}
void update1(ll o,ll l,ll r,ll v)//相乘
{
	if(p[o].left>=l&&p[o].right<=r)
	{
		p[o].value=(p[o].value*v)%mod;
		p[o].lazy=(p[o].lazy*v)%mod;
		p[o].lazy1=(p[o].lazy1*v)%mod;
		return ;
	}
	push_down(o);
	ll mid=(p[o].left+p[o].right)>>1;
	if(r<=mid)
		update1(lson,l,r,v);
	else if(l>mid)
		update1(rson,l,r,v);
	else
	{
		update1(lson,l,mid,v);
		update1(rson,mid+1,r,v);
	}
	push_up(o);
}
ll query(ll o,ll l,ll r)
{
	if(p[o].left>=l&&p[o].right<=r)
		return p[o].value;
	ll mid=(p[o].left+p[o].right)>>1;
	push_down(o);
	if(r<=mid)
		return query(lson,l,r);
	else if(l>mid)
		return query(rson,l,r);
	else
		return query(lson,l,mid)+query(rson,mid+1,r);
}
int main(int argc, char const *argv[])
{
	ios::sync_with_stdio(false);
	scanf("%d%d%d",&n,&m,&mod);
	build(1,1,n);
	int _;
	ll a,b,c;
	while(m--)
	{
		scanf("%d",&_);
		if(_==3)
		{
			scanf("%lld%lld",&a,&b);
			printf("%lld\n",query(1,a,b)%mod);
		}
		else if(_==2)
		{
			scanf("%lld%lld%lld",&a,&b,&c);
			update(1,a,b,c);
		}
		else if(_==1)
		{
			scanf("%lld%lld%lld",&a,&b,&c);
			update1(1,a,b,c);
		}
	}
	return 0;
}