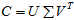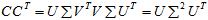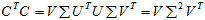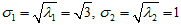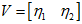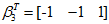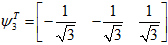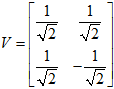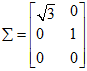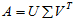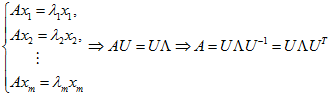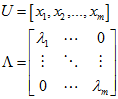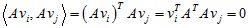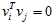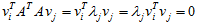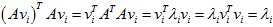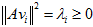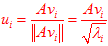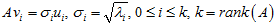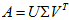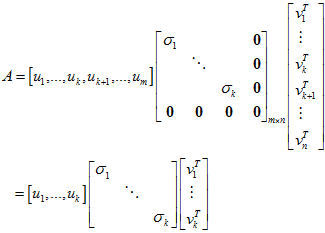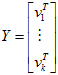奇异分解(SVD)
奇异分解
假设C是m×n矩阵,U是m×m矩阵,其中U的列为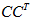
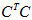
其中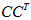
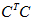
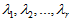
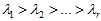
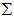
×n的矩阵,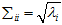
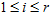
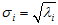
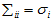
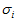
所以有了矩阵C,可以求得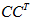
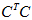
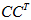
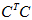
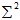
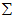
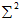
例题:
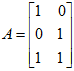
解:
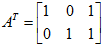
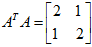
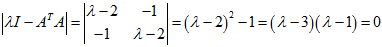
故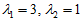
当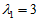
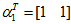
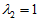
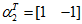
标准化后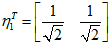
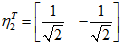
同理,先求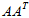
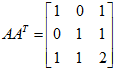
当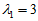
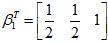
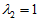
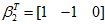
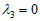
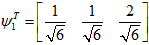
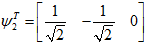
由此可知,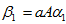
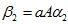
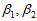
所以
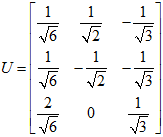
最后得
---------------------------------------------------------------------------------
特征值分解——EVD
在这里,选择一种特殊的矩阵——对称阵(酉空间中叫hermite矩阵即厄米阵)。对称阵有一个很优美的性质:它总能相似对角化,对称阵不同特征值对应的特征向量两两正交。一个矩阵能相似对角化即说明其特征子空间即为其列空间,若不能对角化则其特征子空间为列空间的子空间。现在假设存在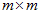
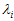
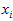
U为的列是两两正交向量,所以它的逆矩阵等于转置矩阵。
奇异值分解——SVD
假设存在一个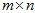
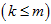
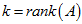
假设这组标准正交基为: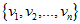
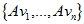
根据假设,也有以下关系:
所以如果选择v为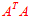
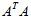
这样就找到了正交基使其映射后还是正交基了,现在,将映射后的正交基单位化:
所以
单位化:
由此得到关系:
从而得到
令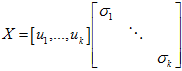
则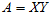
Reference
http://blog.csdn.net/zhongkejingwang/article/details/43053513
奇异分解(SVD)的更多相关文章
- 使用矩阵分解(SVD)实现推荐系统
http://ling0322.info/2013/05/07/recommander-system.html 这个学期Web智能与社会计算的大作业就是完成一个推荐系统参加百度电影推荐算法大赛,成绩按 ...
- 多维数组分解----SVD在推荐系统中的应用-
http://www.janscon.com/multiarray/rs_used_svd.html [声明]本文主要参考自论文<A SINGULAR VALUE DECOMPOSITION A ...
- SVD分解及线性最小二乘问题
这部分矩阵运算的知识是三维重建的数据基础. 矩阵分解 求解线性方程组:,其解可以表示为. 为了提高运算速度,节约存储空间,通常会采用矩阵分解的方案,常见的矩阵分解有LU分解.QR分解.Cholesky ...
- SVD神秘值分解
SVD分解 SVD分解是LSA的数学基础,本文是我的LSA学习笔记的一部分,之所以单独拿出来,是由于SVD能够说是LSA的基础,要理解LSA必须了解SVD,因此将LSA笔记的SVD一节单独作为一篇文章 ...
- SVD分解技术数学解释
SVD分解 SVD分解是LSA的数学基础,本文是我的LSA学习笔记的一部分,之所以单独拿出来,是因为SVD可以说是LSA的基础,要理解LSA必须了解SVD,因此将LSA笔记的SVD一节单独作为一篇文章 ...
- PCA本质和SVD
一.一些概念 线性相关:其中一个向量可以由其他向量线性表出. 线性无关:其中一个向量不可以由其他向量线性表出,或者另一种说法是找不到一个X不等于0,能够使得AX=0.如果对于一个矩阵A来说它的列是线性 ...
- 从矩阵(matrix)角度讨论PCA(Principal Component Analysis 主成分分析)、SVD(Singular Value Decomposition 奇异值分解)相关原理
0. 引言 本文主要的目的在于讨论PAC降维和SVD特征提取原理,围绕这一主题,在文章的开头从涉及的相关矩阵原理切入,逐步深入讨论,希望能够学习这一领域问题的读者朋友有帮助. 这里推荐Mit的Gilb ...
- SVD的概念以及应用
第十四章 利用SVD简化数据 一.引言 SVD的全称是奇异值分解,SVD的作用是它能够将高维的数据空间映射到低维的数据空间,实现数据约减和去除噪声的功能. SVD的特点主要有以下几个方面: 1.它的优 ...
- 推荐系统 SVD和SVD++算法
推荐系统 SVD和SVD++算法 SVD: SVD++: [Reference] 1.SVD在推荐系统中的应用详解以及算法推导 2.推荐系统——SVD/SVD++ 3.SVD++ 4.SVD++协 ...
随机推荐
- 【Alpha版本】冲刺阶段——Day3
[Alpha版本]冲刺阶段--Day3 阅读目录 今日进展 问题困难 明日任务 今日贡献量 TODOlist [今日进展] 密码算法方面: 参考了md5/sha1+salt和Bcrypt后,我们决定使 ...
- navicat 连接postgresql报错pg_hba.conf
PostgreSQ数据库为了安全,它不会监听除本地以外的所有连接请求,当用户通过JDBC访问是,会报一些如下的异常: org.postgresql.util.PSQLException: FATAL: ...
- httpclient get post
https://www.cnblogs.com/wutongin/p/7778996.html post请求方法和get请求方法 package com.xkeshi.paymentweb.contr ...
- QT -- plan
QT -- 跨平台的 C++ 图形用户界面 应用程序框架 GUI介绍框架项目文件 .pro第一个QT (hello QT)父窗口 和 子窗口的区别(控件,部件,构件)信号 和 槽(信号的处理 ...
- python URLError,HTTPError 的异常处理
URLError,HTTPError 的异常处理 1. URLErrorURLError产生的原因1). 网络无连接2). 连接不到特定的服务器3). 服务器不存在 # 例子 import urlli ...
- How to use Nissan consult 3 plus to check, make key and program?
How to use Nissan consult 3 plus to test Nissan? Firstly: get one particular Nissan consult 3 plus. ...
- 编写一个JavaWeb项目
基本流程:JSP文件显示页面,在前端页面输入赋值,使用form或href超链接传值到Servlet中方法,在Servlet方法中调用Dao层的类对象,将数据传到数据库中,并实现对数据库里的数据的增删改 ...
- (2018干货系列八)最新VR学习路线整合
怎么学VR 即虚拟现实技术,是一种可以创建和体验虚拟世界的计算机仿真系统,它利用计算机生成一种模拟环境,是一种多源信息融合的.交互式的三维动态视景和实体行为的系统仿真使用户沉浸到该环境中.VR/AR/ ...
- echo 换行与否
echo默认是有换行的, -n的时候, 是不换行的.
- Opencv改变图像亮度和对比度以及优化
https://blog.csdn.net/u013139259/article/details/52145377 版权声明:本文为博主原创文章,未经博主允许不得转载. https://blog.cs ...