【魔改】莫队算法+组合数公式 杭电多校赛4 Problem B. Harvest of Apples

http://acm.hdu.edu.cn/showproblem.php?pid=6333

莫队算法是一个离线区间分块瞎搞算法，只要满足：1.离线  2.可以O（1）从区间（L,R）更新到（L±1，R±1）就能直接套板子了

这道题不是区间算法，但是有递推式：

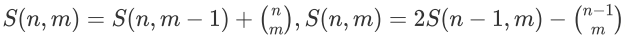
把它看成区间更新orz

所以可以莫队orz

#define _CRT_SECURE_NO_WARNINGS
#include    <cmath>
#include <iostream>
#include    <stdio.h>
#include<algorithm>
#include        <map>
#include     <cstring>
#include      <time.h>
using namespace std;
#define rep(i,t,n)  for(int i =(t);i<=(n);++i)
#define per(i,n,t)  for(int i =(n);i>=(t);--i)
#define mmm(a,b) memset(a,b,sizeof(a))
const int maxn = 1e5 + ;
const long long mod = 1e9 + ;
map<int, int> mmp;
typedef long long ll;
struct node {
    int l, r, id;
 
}Q[maxn];
ll fac[maxn], infac[maxn];
long long ans[maxn];
long long num[maxn];
int a[maxn], pos[maxn];
int n, m, k;
int L = , R = ;
long long Ans = ;
 
ll cal(ll x) {
    ll res = ;
    int k = mod - ;
    while (k) {
        if (k & ) {
            res *= x;
            res %= mod;
        }
        x *= x;
        x %= mod;
        k >>= ;
    }
    return res;//cal(x^ mod)
}
void init() {
    fac[] = ;
    rep(i, , maxn - )fac[i] = (fac[i-] * i)%mod;
    rep(i, , maxn - )infac[i] = cal(fac[i]);
}
ll C(ll a, ll b)
{
    return 1ll * fac[a] * infac[b] % mod * infac[a - b] % mod;
}
bool cmp(node a, node b) {
    if (pos[a.r] == pos[b.r])
        return a.l < b.l;
    return pos[a.r] < pos[b.r];
 
}
void add(int x) {
 
    //num[a[x]]++;
    //if (num[a[x] - 1] == 0 && num[a[x] + 1] == 0)Ans++;
    //else if (num[a[x] - 1] && num[a[x] + 1])Ans--;
    Ans += C(n, m);
 
}
void addl(int x) {
 
}
void del(int x) {
    //num[a[x]]--;
    //if (num[a[x] - 1] == 0 && num[a[x] + 1] == 0)Ans--;
    //else if (num[a[x] - 1] && num[a[x] + 1])Ans++;
    Ans -= C(n, m + );
}
 
int smain() {
    int t; scanf("%d", &t);
    init();
        Ans = ;
        mmm(num, );
        L = , R = ;
 
        int sz = sqrt(1e5);
        for (int i = ; i <= 1e5; i++) {
            pos[i] = i / sz;
        }
 
        rep(i,,t) {
            scanf("%d%d", &Q[i].l, &Q[i].r);
            Q[i].id = i;
        }
        sort(Q + , Q +  + t, cmp);
        Ans = ;//S(m,n
        L = Q[].l; R = -;
        rep(i,,t){
            while (L < Q[i].l) {
                //del(L);
                Ans = (2ll * Ans - C(L, R) + mod) % mod;
                ++L;
            }
 
            while (L > Q[i].l) {
                --L;
                //addl(L);
                Ans = ((Ans + C(L, R)) *infac[]%mod) % mod;
            }
 
            while (R < Q[i].r) {
                ++R;
                //add(R);
                Ans = (Ans+C(L, R))%mod;
            }
            while (R > Q[i].r) {
                //del(R);
                Ans = (Ans-C(L, R)+mod)%mod;
                --R;
 
            }
 
            ans[Q[i].id] = Ans;
        }
        rep(i,,t)printf("%lld\n", ans[i]);
    return ;
}
/*
 
6
60522 25373
36426 3283
48772 42553
33447 12441
3497 2182
7775 4025
 
*/
#define ONLINE_JUDGE
int main() {
    //ios::sync_with_stdio(false);
#ifndef ONLINE_JUDGE
    FILE *myfile;
    myfile = freopen("C:\\Users\\acm-14\\Desktop\\test\\b.in", "r", stdin);
    if (myfile == NULL)
        fprintf(stdout, "error on input freopen\n");
    FILE *outfile;
    outfile = freopen("C:\\Users\\acm-14\\Desktop\\test\\out.txt", "w", stdout);
    if (outfile == NULL)
        fprintf(stdout, "error on output freopen\n");
    long _begin_time = clock();
#endif
    smain();
#ifndef ONLINE_JUDGE
    long _end_time = clock();
    printf("time = %ld ms.", _end_time - _begin_time);
#endif
    cin >> n;
    return ;
}