基于GPS数据建立隐式马尔可夫模型预测目的地

　　《Trip destination prediction based on multi-day GPS data》是一篇在2019年，由吉林交通大学团队发表在elsevier期刊上的一篇论文。在论文中，他们基于GPS数据，使用不同的方法建立了多个预测目的地的模型，进行对比试验，最终提高了正确率，取得了很好的效果。

0. 概括

　　基于8周、10人的GPS数据，在隐式马尔可夫模型和习惯预测模型的基础上，作者建立了一个可以预测出行目的地的模型，该模型大大提高了预测的精度。最重要的他们发现，人们出行关于终点的选择不仅依赖于终点和起点的依赖关系，而是在连续多天、多周中出行的惯性。他们对于这一点做了实验，最后证明了惯性，在周末是决定两个相邻的位置是否是终点的最重要因素，在工作日是决定连续多天出行的重要因素。

1. 引言

第二部分对于相关工作进行了介绍；第三部分介绍了GPS数据的预处理工作和关于终点选择的基本特征；第四部分介绍了这个使用马尔可夫链和基于喜好的pre-trip终点预测模型；第五部分他们介绍了隐式的马尔可夫模型，用于建立during-trip终点预测模型；第六部分对于文章内容做了总结，并进行了展望。

在引言中提到了两类终点预测模型，pre-trip和during-trip，也就是在旅途前和在旅途中进行重点预测。前者可以用于拥挤位置预测与分析（crowded location forecasting and analyzing），后者可以用于GPS导航，可以自动为用户推荐一些地点。

2. 研究现状

Ashbrook and Starner’s study [2]第一次提出使用马尔可夫模型基于GPS数据预测终点；Ashbrook et al.[3]提出了使用隐式的马尔可夫模型预测终点，结果大幅提高了精度。但是这篇文章中的精度并不稳定，从70%~94%都有。作者认为可能是由于没有考虑周末和工作日；Alvarez-Garcia et al.[1]也提出了一种基于隐式的马尔可夫链的预测模型，这个模型考虑进去了更多的特征例如支持点、访问频率等。Huang et al.[4]除了使用gps数据，还考虑了其他的因素例如地理、社会经济信息等，他建立了一Mixed-effects logit模型；还有一些研究者使用贝叶斯推理、使用相邻的道路推理、使用行程的特征推理等等。

根据统计的结果，作者将惯性定义为由以下三个与以往习惯相关的因素：相邻终点之间的惯性，相邻天之间的惯性，以及相邻周之间的惯性（主要是指，比如，每周一都要去超市买菜，每周日都要去教堂做礼拜之类的情景）。他利用这三个因素作为预测模型的三个变量，改善了pre-trip模型，除此之外，他利用支持点（the support points）用于during-trip预测，用于保存和继续调整模型。最后他将时间分为周末和工作日再次训练预测模型。

3. 数据处理

数据来源：数据集来自2017年长春10位志愿者提供的连续8周的GPS数据。前六周的数据用于训练，后两周的模型用于测试结果。除此之外，还让10位志愿者填写了调查问卷，用于测试和训练结果。

数据处理：首先，根据时间长度、速度、区域范围，对于GPS数据进行筛选；之后，确定经常访问的区域；最后将数据集根据工作日和周末再分开。

分析区域的访问频率：这是数据处理的一个步骤，作者对于这一部分进行了详细说明。区域的访问频率，作者分为了三类：同一天内、一周内、多周内。对于同一天内的访问频率统计，作者将一天划分成了5个时段进行统计；对于同一周内的访问频率统计，作者将一周划分成工作日和周末两中情况，分别对这两种情况的每一天的相同时段的次数进行统计；对于多周之间的统计，统计不同周的相同星期的相同时间的访问次数。

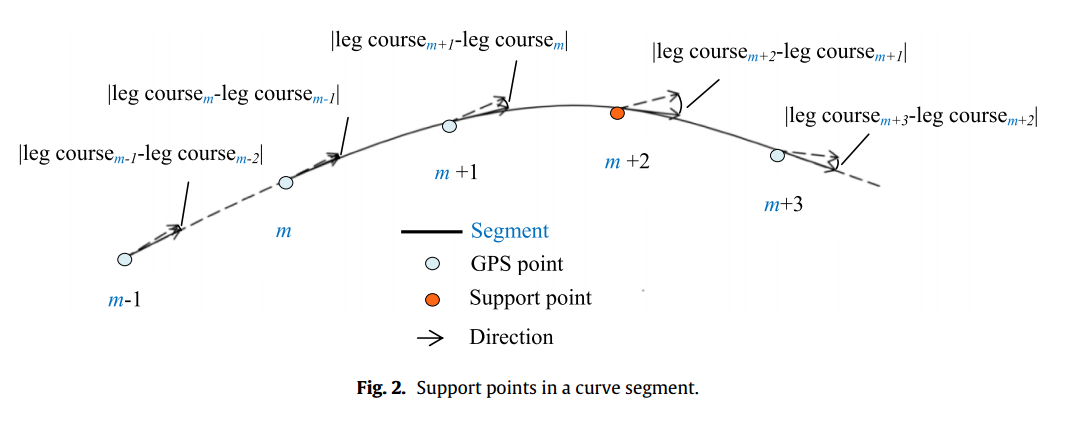
确定支持点（the support points）：支持点是具有特殊的特征的GPS点，用于GPS数据处理，可以代表某一路线。某一直路线含有一到两个支持点，每条曲路线只有一个支持点。文章中给出了一种求支持点的方法。根据引用的文献[19,20]，由于道路网络中相邻交叉点的距离是500m，所以选择500m作为阈值。在计算直路线的支持点时，如果路线L(m,n)长度小于500米时，选择第(m+n)/2个点作为L(m,n)的支持点，如果长度大于500米，那么选择第m+3个点和第n-3个点作为这段路线的支持点。如果GPS数据点中超过连续四个点的步长小于30，那么说明这是一条曲路线。对于曲路线，选择相对于最后一个点，步长变化最大的一个点作为支持点。Fig.1 和Fig.2给出了两种求支持点路线的示意图。

4. pre-trip终点预测

通过之前的工作，得到了不同地区的访问频率，这样就可以检验作者上文中定义的惯性——相邻终点之间的惯性，相邻天之间的惯性，以及相邻周之间的惯性。在相邻终点中间的惯性使用马尔可夫链进行调整；在相邻天和相邻周之间的惯性可以用之前得到的不同种类的访问频率表示。基于多项式逻辑模型，对三个习惯相关因素的影响进行定量比较。然后，将通过考虑所有三个因素来预测出行前目的地。

作者基于马尔可夫链和习惯模型（Habit-based model）完成了pre-trip终点预测。

马尔可夫链：使用访问频率矩阵，矩阵规模是N*N，N表示该用户访问的终点个数，以及初始状态矩阵，矩阵规模也是N*N。前六周的GPS数据用于调整马尔可夫链，根据初始状态矩阵和在之前得到的访问频率较高的终点矩阵S（具体内容见论文4.1节，这里只是大致说一下）可以得到最终的结果，转移概率矩阵A。然后使用后两周的数据进行测试，工作日和周末的预测正确率是74%和63%，作者推测原因是人们在工作日的出行更具有规律。

习惯模型：为了提高马尔可夫链的精度，加入用户之前的旅游习惯进行分析，不仅仅只考虑相邻区域之间的转移惯性，加入了相邻天和相邻周之间的惯性作为变量。使用多项式逻辑模型（MNL）完成上述工作。作者在MNL中加入马尔可夫转移概率和一周内、多周内的不同地点的访问频率作为参数进行训练。

5.during-trip重点预测

为了实现实时的预测，作者使用隐式的马尔可夫模型（HMM）进行训练，根据之前统计的不同地区的访问频率和支持点，设置初始状态和参数，（具体过程见论文5.1节）可以让我们得到GPS数据序列的隐藏状态，也就是实时的终点。根据HMM的估计结果，频繁访问的目的地具有最大的转移概率被确定为下一个目的地。最终结果显示在工作日和周末的重点预测中，正确率分别是91%和85%，相比马尔可夫链模型有了显著的提高，这说明了引入支持点对于正确率有很大的效果。但是想比习惯模型，在工作日的预测正确率却没有显著的提高，作者认为，这说明了在工作日引入支持点和使用惯性进行预测的效果相同。所以，实验证明了，在周末这种经常进行不是很有规律的出行的情况下，引入支持点的效果比使用惯性进行预测的效果更好。

6. 总结

作者将周末和工作日的数据分开，使用马尔可夫模型、MNL模型对于pre-trip终点预测进行了实现；使用隐式马尔可夫模型对于during-trip终点预测模型进行了实现。最终正确率相比之前的研究取得了很好的效果。

作者说，这篇论文的局限是没有考虑到可能影响出行目的地的因素选择，如交通状况和一些管理策略，如区域拥堵收费。实时交通状况和交通管理政策将是今后研究的重点之一。在除了预测出行目的地外，预测出行路线也非常重要，其中与习惯有关的因素也应该考虑。在未来的研究中，作者将尝试利用收集到的多日目的地选择数据在其他城市，对本文的结果进行验证。