java实现二叉树的前中后遍历（递归和非递归）

这里使用下图的二叉树作为例子：

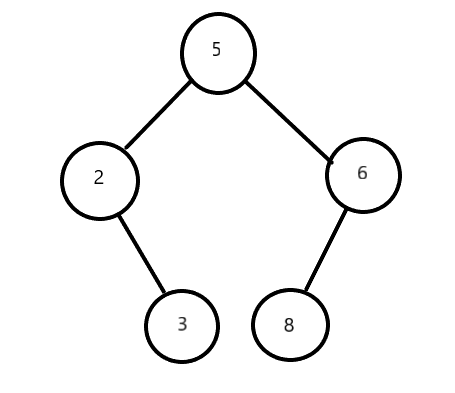
首先建立树这个类：

public class Node {
    private int data;
    private Node leftNode;
    private Node rightNode;

    public Node(int data, Node leftNode, Node rightNode) {
        this.data = data;
        this.leftNode = leftNode;
        this.rightNode = rightNode;
    }

    public int getData() {
        return data;
    }

    public void setData(int data) {
        this.data = data;
    }

    public Node getLeftNode() {
        return leftNode;
    }

    public void setLeftNode(Node leftNode) {
        this.leftNode = leftNode;
    }

    public Node getRightNode() {
        return rightNode;
    }

    public void setRightNode(Node rightNode) {
        this.rightNode = rightNode;
    }
}

使用递归的方式遍历二叉树，这种遍历虽然比较简单，但涉及到递归的算法都尽量慎用！

//递归遍历二叉树
public class RecursionBinaryTree {

    //先建立子节点，再建立父节点
    public Node init(){
        Node E = new Node(8,null,null);
        Node C = new Node(6,E,null);
        Node D = new Node(3,null,null);
        Node B = new Node(2,D,null);
        Node A = new Node(7, B, C);
        return A;   //返回根节点
    }

    public void printNode(Node node){
        System.out.print(node.getData());
    }
    //先序遍历:根左右的顺序遍历二叉树
    public void firstTraversal(Node root){
        printNode(root);    //输出根节点数据
        if(root.getLeftNode()!=null){
            firstTraversal(root.getLeftNode());
        }
        if(root.getRightNode()!=null){
            firstTraversal(root.getRightNode());
        }
    }
    //中序遍历：左根右
    public void inOrderTraversal(Node root){
        if(root.getLeftNode()!=null){
            inOrderTraversal(root.getLeftNode());
        }
        printNode(root);
        if(root.getRightNode()!=null){
            inOrderTraversal(root.getRightNode());
        }
    }

    //后序遍历：左右根
    public void postOrderTraversal(Node root){
        if(root.getLeftNode()!=null){
            postOrderTraversal(root.getLeftNode());
        }
        if(root.getRightNode()!=null){
            postOrderTraversal(root.getRightNode());
        }
        printNode(root);
    }

    public static void main(String[] args) {
        RecursionBinaryTree tree = new RecursionBinaryTree();
        Node root = tree.init();
        System.out.println("先序遍历：");
        tree.firstTraversal(root);
        System.out.println();
        System.out.println("中序遍历：");
        tree.inOrderTraversal(root);
        System.out.println();
        System.out.println("后序遍历：");
        tree.postOrderTraversal(root);
    }
}

再看看使用非递归的方式遍历二叉树，面试的时候会经常问到使用非递归的方式实现二叉树的中序遍历。

//堆栈遍历二叉树
public class StackBinaryTree {

    public Node init(){
        Node E = new Node(8,null,null);
        Node C = new Node(6,E,null);
        Node D = new Node(3,null,null);
        Node B = new Node(2,D,null);
        Node A = new Node(5, B, C);
        return A;   //返回根节点
    }

    public void printNode(Node node){
        System.out.print(node.getData());
    }
    //先序遍历：根左右
    public void firstTraversal(Node root){
        Stack<Node> stack = new Stack<>(); //定义一个栈
        while (root!=null||stack.size()>0){     //判断节点是否为空或者栈中是否为空，当均为空时，结束循环
            if(root!=null){
                printNode(root);
                stack.push(root);
                root = root.getLeftNode();
            }else {
                root = stack.pop();
                root = root.getRightNode();
            }
        }
    }

    //中序遍历：左根右
    public void inOrderTraversal(Node root){
        Stack<Node> stack = new Stack<>(); //定义一个栈
        while (root!=null||stack.size()>0){
            if(root!=null){
                stack.push(root);   //直接压入栈
                root = root.getLeftNode();
            }else {
                root = stack.pop(); //出栈时输出下
                printNode(root);
                root = root.getRightNode();
            }
        }
    }

    public void postOrderTraversal(Node root){
        Stack<Node> stack = new Stack<>();
        Stack<Node> output = new Stack<>();//构造一个中间栈存储后序遍历的结果
        while (root!=null||stack.size()>0){
            if(root!=null){
                output.push(root);
                stack.push(root);
                root = root.getRightNode();
            }else {
                root = stack.pop();
                root = root.getLeftNode();
            }
        }
        while (output.size()>0){
            printNode(output.pop());
        }
    }

    public static void main(String[] args) {
        StackBinaryTree tree = new StackBinaryTree();
        Node root = tree.init();
        System.out.println("先序遍历：");
        tree.firstTraversal(root);
        System.out.println("中序遍历：");
        tree.inOrderTraversal(root);
        System.out.println("后序遍历：");
        tree.postOrderTraversal(root);
    }
}