[ZJOI2006]物流运输 SPFA+DP

题目描述

物流公司要把一批货物从码头A运到码头B。由于货物量比较大，需要n天才能运完。货物运输过程中一般要转停好几个码头。物流公司通常会设计一条固定的运输路线，以便对整个运输过程实施严格的管理和跟踪。由于各种因素的存在，有的时候某个码头会无法装卸货物。这时候就必须修改运输路线，让货物能够按时到达目的地。但是修改路线是—件十分麻烦的事情，会带来额外的成本。因此物流公司希望能够订一个n天的运输计划，使得总成本尽可能地小。

输入输出格式

输入格式：

第一行是四个整数n(l≤n≤100)、m(l≤m≤20)、K和e。n表示货物运输所需天数，m表示码头总数，K表示每次修改运输路线所需成本。接下来e行每行是一条航线描述，包括了三个整数，依次表示航线连接的两个码头编号以及航线长度(>0)。其中码头A编号为1，码头B编号为m。单位长度的运输费用为1。航线是双向的。再接下来一行是一个整数d，后面的d行每行是三个整数P(1<P<m)，a，b(1≤a≤b≤n)。表示编号为P的码头从第a天到第b天无法装卸货物（含头尾）。同一个码头有可能在多个时间段内不可用。但任何时间都存在至少一条从码头A到码头B的运输路线。

输出格式：

包括了一个整数表示最小的总成本。总成本=n天运输路线长度之和+K*改变运输路线的次数。

输入输出样例

输入样例#1：

输出样例#1：

说明

【样例输入说明】

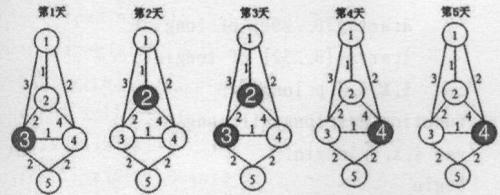
上图依次表示第1至第5天的情况，阴影表示不可用的码头。

【样例输出说明】

前三天走1-4-5，后两天走1-3-5，这样总成本为(2+2)*3+(3+2)*2+10=32。

题解：

我们先预处理出从[L,R]这几天中&&在满足某些点不能走的情况下的最短路，记为C[N][N];

于是可以进行DP：

设F[I]为前i天的最小总成本，可以得出： F[i]=min(F[i],F[j]+c[j+1][i]*(i-j)+k) k为改变线路所需的费用，（i-j）为这一段时间内的天数

具体看代码:

 #include<iostream>

 #include<cstdio>

 #include<cstring>

 #include<algorithm>

 #include<cmath>

 #include<cstdlib>

 #include<ctime>

 #include<queue>

 using namespace std;

 typedef long long ll;

 const int N=,M=;

 int n,m,k,day;

 int gi()

 {

     int str=;bool f=;char ch=getchar();

     while(ch>''||ch<''){if(ch=='-')f=-;ch=getchar();}

     while(ch>='' && ch<='')str=str*+ch-'',ch=getchar();

     return str*f;

 }

 const int INF=;

 struct Lin

 {

     int next,to,dis;

 }a[N*N*];

 bool vis[N];

 int head[N],num=;int c[N][N],f[N];

 bool nort[];

 bool d[][N];

 int F[N];

 void spfa(int from,int to)//表示从第from天到to天

 {

     int x,u;

     queue<int>q;

     q.push();

     for(int i=;i<=n;i++)f[i]=INF,vis[i]=false;

     vis[]=true;f[]=;

     while(!q.empty())

     {

         x=q.front();q.pop();

         for(int i=head[x];i;i=a[i].next){

             u=a[i].to;

             if(!nort[u]){//如果该点在from-to中不能通行则不能加入队列

                 if(f[x]+a[i].dis<f[u]){

                     f[u]=f[x]+a[i].dis;

                      if(!vis[u]){

                         vis[u]=true;q.push(u);

                     }

                 }

             }

         }

         vis[x]=false;

     }

     c[from][to]=f[n];

 }

 void init(int x,int y,int z)

 {

     a[++num].next=head[x];

     a[num].to=y;

     a[num].dis=z;

     head[x]=num;

 }

 int main()

 {

     int x,y,z;

     day=gi();n=gi();k=gi();m=gi();

     for(int i=;i<=m;i++){

         x=gi();y=gi();z=gi();

         init(x,y,z);init(y,x,z);

     }

     int ppap=gi(),ls,rs;

     for(int i=;i<=ppap;i++){

         x=gi();ls=gi();rs=gi();

         for(int j=ls;j<=rs;j++)d[x][j]=true;

     }

     for(int i=;i<=day;i++){//预处理

         memset(nort,,sizeof(nort));

         for(int j=i;j<=day;j++){

             for(int k=;k<=n;k++)nort[k]|=d[k][j];

             spfa(i,j);

         }

     }

     memset(F,/,sizeof(F));

     F[]=-k;

     for(int i=;i<=day;i++){

         for(int j=;j<=i-;j++)

         if(c[j+][i]!=INF)

         F[i]=min(F[i],F[j]+c[j+][i]*(i-j)+k);

     }

     printf("%d",F[day]);

     return ;

 }