Python函数学习——递归

递归函数

在函数内部，可以调用其他函数。如果一个函数在内部调用自身本身，这个函数就是递归函数。

函数实现过程

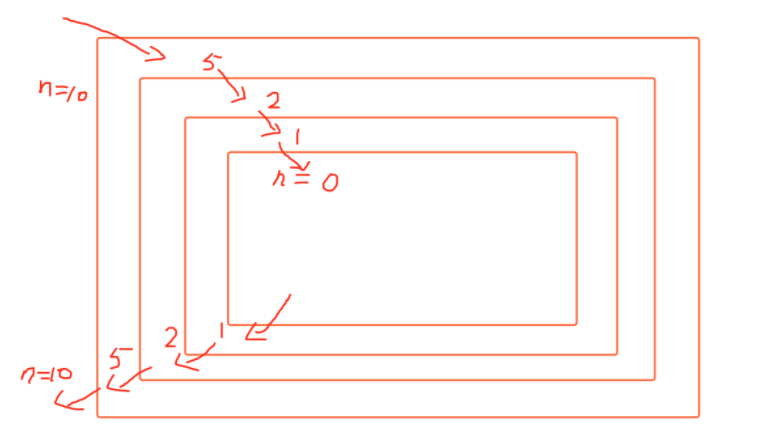
def calc(n):
    v = int(n//2)
    print(v)
    if v > 0:
        calc(v)
    print(n)

calc(10)

输出结果

5
2
1
0
1
2
5
10

为什么是这个结果

递归特性:

1. 必须有一个明确的结束条件
2. 每次进入更深一层递归时，问题规模相比上次递归都应有所减少
3. 一般通过return结束递归
4. 递归效率不高，递归层次过多会导致栈溢出（在计算机中，函数调用是通过栈（stack）这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，会导致栈溢出）
5. 堆栈扫盲http://www.cnblogs.com/lln7777/archive/2012/03/14/2396164.html

递归深度

python默认对最大递归层数做了一个限制：997，但是也可以自己限制

import sys
sys.setrecursionlimit(10000)#修改递归层数
n=0
def f():
    global n
    n+=1
    print(n)
    f()
f()

递归应用

1.下面我们来猜一下小明的年龄

小明是新来的同学，丽丽问他多少岁了。

他说：我不告诉你，但是我比滔滔大两岁。

滔滔说：我也不告诉你，我比晓晓大两岁

晓晓说：我也不告诉你，我比小星大两岁

小星也没有告诉他说：我比小华大两岁

最后小华说，我告诉你，我今年18岁了

这个怎么办呢？当然，有人会说，这个很简单啊，知道小华的，就会知道小星的，知道小星的就会知道晓晓的，以此类推，就会知道小明的年龄啦。这个过程已经非常接近递归的思想了。

用递归实现

"""
age(5) = age(4)+2
age(4) = age(3) + 2
age(3) = age(2) + 2
age(2) = age(1) + 2
age(1) = 18
"""

def calc_age(n):
    if n == 1:
        return 18
    else:
        return calc_age(n-1)+2

print(calc_age(5)) #

2.一个数，除2直到不能整除2

n = 100
def cal(n):
    if n == 0:
        return
    else:
        n = int(n // 2)
        print(n)
        cal(n)
        print("退出=", n)
cal(100)

3.一个数，除2直到次数等于5退出

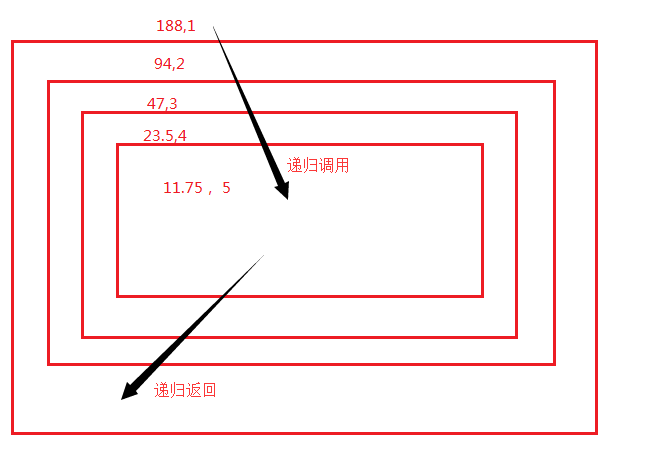
def calc(n,count):
    print(n, count)
    if count < 5:
        r = calc(n / 2, count + 1)
        return r  # 里层返回为上层,此处不加return 返回None
    else:
        return n # 最里层返回

res = calc(188, 1)
print('res ', res)

递归调用过程

4.深度查询

menus = [
    {
        'text': '北京',
        'children': [
            {'text': '朝阳', 'children': []},
            {'text': '昌平', 'children': [
                {'text': '沙河', 'children': []},
                {'text': '回龙观', 'children': []},
            ]},
        ]
    },
    {
        'text': '上海',
        'children': [
            {'text': '宝山', 'children': []},
            {'text': '金山', 'children': []},
        ]
    }
]
#  深度查询
#1. 打印所有的节点
#2. 输入一个节点名字，沙河， 你要遍历找，找到了，就打印它，并返回true,

实现

# 打印所有的节点
def recu_Menu(menu):
    for sub_menu in menu:
        menu_text = sub_menu['text']
        menu_children = sub_menu['children']
        print(menu_text)
        recu_Menu(menu_children)

recu_Menu(menus)

# 打印所有的节点,输入一个节点名字，沙河， 你要遍历找，找到了，就打印它，并返回true,
def recu_Menu_node(menu, node, layer):
    # if len(menu)>0:
    for sub_menu in menu:
        menu_text = sub_menu['text']
        menu_children = sub_menu['children']
        print("menu_text=", menu_text)
        if node == menu_text:
            print("找到%s在第%s层" % (node, layer)) #返回到外层
            return True
        else:
            if recu_Menu_node(menu_children, node, layer + 1) == True: #如果里层返回True，继续向上返回True
                return True
            else:
                recu_Menu_node(menu_children, node, layer + 1)
node_str = input("输入一个节点名字-> ")
print(recu_Menu_node(menus, node_str, 1))

-》回龙观

找到回龙观在第3层
True

5.猴子吃桃问题

# 题目：猴子吃桃问题：猴子第一天摘下若干个桃子，当即吃了一半，还不瘾，又多吃了一个
#  第二天早上又将剩下的桃子吃掉一半，又多吃了一个。
#  以后每天早上都吃了前一天剩下的一半零一个。
#  到第10天早上想再吃时，见只剩下一个桃子了。求第一天共摘了多少。

"""
下一天等于是前一天吃了一半还多一个剩下的。
所以f(n) = 2 * f(n - 1) + 2
"""
def peach(n):
    if n == 1:
        return 1
    else:
        return 2 * peach(n-1) + 2

print(peach(10))  #

6.二分查找算法

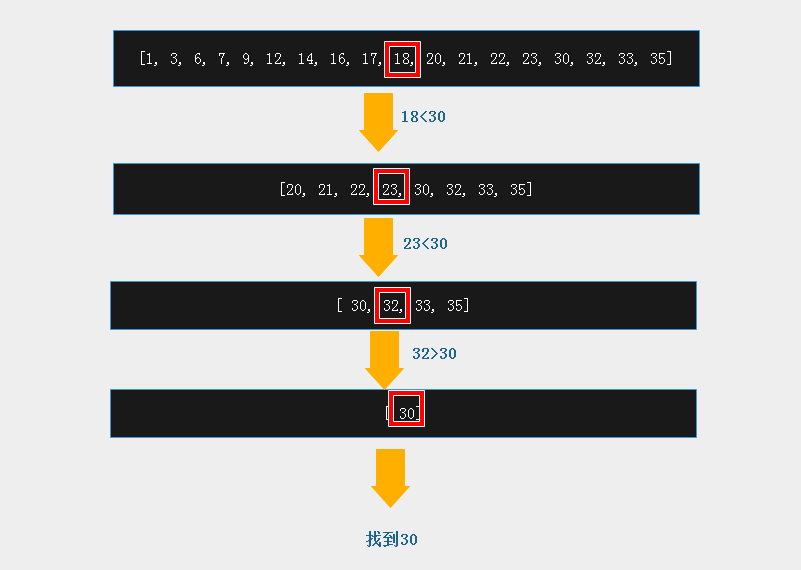
从[1, 3, 6, 7, 9, 12, 14, 16, 17, 18, 20, 21, 22, 23, 30, 32, 33, 35]序列中找到30的位置

代码实现

data = [1, 3, 6, 7, 9, 12, 14, 16, 17, 18, 20, 21, 22, 23, 30, 32, 33, 35]
print('start to find')

# 递归二分查找
def binary_search(dataset, start, end, val):
    mid = int((start + end)/ 2)  # 取中间数
    # print(dataset, mid, start, end)
    if start <= end:
        if dataset[mid] == val:  # 判断中间值和要找的那个值的大小关系
            print("find val", dataset[mid])
            return mid
        elif dataset[mid] > val:
            print('mid %s is bigger than %s, keep looking in left %s' % (dataset[mid], val, mid))
            return binary_search(dataset, start, mid-1, val)
        else:  # dataset[mid] < val:
            print('mid %s is smaller than %s, keep looking in right %s' % (dataset[mid], val, mid))
            return binary_search(dataset, mid+1, end, val)
    else:
        # if dataset[start] == val:
        #     print('finally find val:', dataset[start])
        #     return start
        # else:
            print("data %s doesn't exist in dataset " % val)
            return -1

print('start to find')
print(binary_search(data,0,len(data)-1, 30))

输出结果

start to find
mid 17 is smaller than 30, keep looking in right 8
mid 23 is smaller than 30, keep looking in right 13
mid 32 is bigger than 30, keep looking in left 15
find val 30
mid =14 #返回位置为14

另一种实现

data = [1, 3, 6, 7, 9, 12, 14, 16, 17, 18, 20, 21, 22, 23, 30, 32, 33, 35]
print('start to find')
def binary_search(dataset, val):
    mid = int(len(dataset)/ 2)  # 取中间数
    print(dataset)
    if mid > 0:
        if dataset[mid] == val:  # 判断中间值和要找的那个值的大小关系
            print("find n", dataset[mid])
        elif dataset[mid] > val:
            new_dataset = dataset[:mid]  # 顾头不顾尾
            print('mid %s is bigger than %s, keep looking in left %s' % (dataset[mid], val, mid))
            binary_search(new_dataset, val)
        else: # dataset[mid] < val:
            new_dataset = dataset[mid:]  # 顾头不顾尾
            print('mid %s is smaller than %s, keep looking in right %s' % (dataset[mid], val, mid))
            binary_search(new_dataset, val)
    else:
        if dataset[0] == val:
            print('finally find val:', dataset[0])
        else:
            print("data %s doesn't exist in dataset " % val)

binary_search(data,30)