uvalive 5834 Genghis Khan The Conqueror

题意：

给出一个图，边是有向的，现在给出一些边的变化的信息（权值大于原本的），问经过这些变换后，MST总权值的期望，假设每次变换的概率是相等的。

思路：

每次变换的概率相等，那么就是求算术平均。

首先求出最小生成树，若变换的边不在最小生成树上，那么就不用管；如果在，那么就需要求变换之后的MST的总权值，有两种情况，第一是继续使用变换后的边，还是MST，第二是放弃这条边，使用其它边构成MST。取两者中的最小值。

第二种情况需要较为深入的讨论，如何使得在较优的时间内找到一条边，使得这条边加入后还是MST。

放弃了一条边之后，MST就变成了两棵最小生成子树，那么要找的边实际就是两棵树之间的最短距离，就转化成了求两棵树之间的最短距离。

如何求两棵树的最短距离，树形dp，这个我也是看题解学习的Orz。具体的做法是每次用一个点作为根，在dfs的过程中，将每一条非树边对最短距离进行更新，这个最短距离对应的是去掉dfs中每一对点所连的边的形成的两棵子树。

看图

红色的是非树边，那么这条非树边就可以更新去掉点A与点B连的树边之后形成的两棵树的最小距离，也可以更新去掉点B与点C连的树边后形成的两棵树的最小距离。每次dfs访问n个点，n次dfs，所以复杂度为O(n^2)。

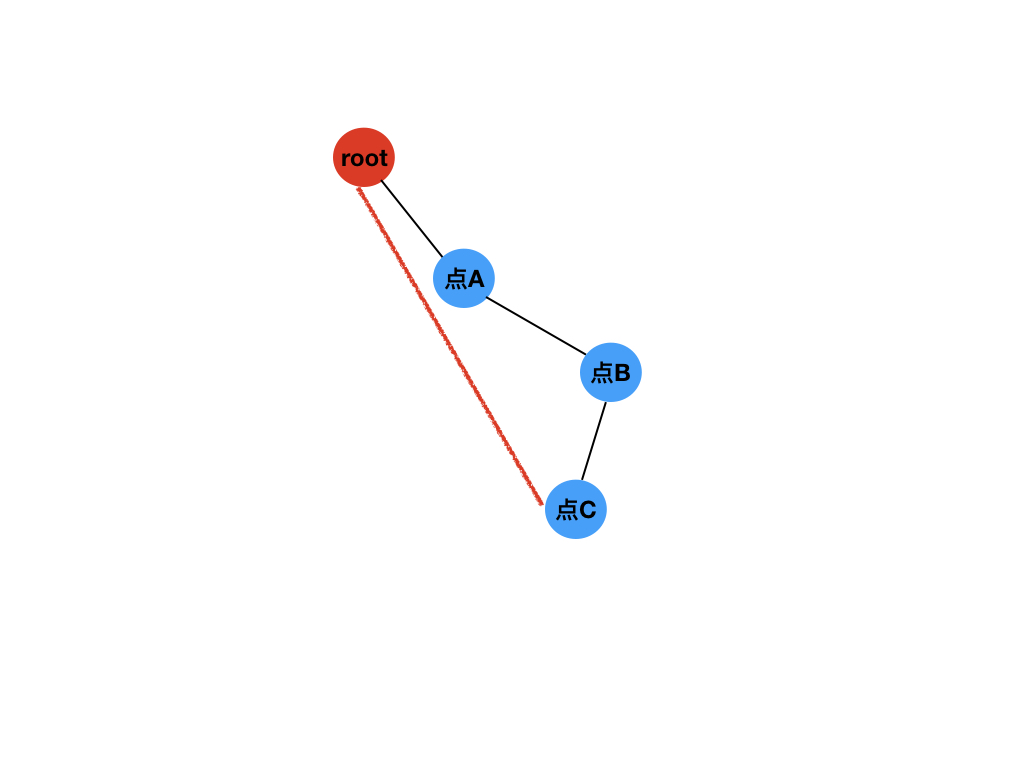
总复杂度为O(n^2)。

代码：

 #include <stdio.h>
 #include <string.h>
 #include <algorithm>
 #include <vector>
 using namespace std;

 const int N = ;
 const int inf = 0x3f3f3f3f;

 int mp[N][N],pre[N];
 bool used[N][N];
 int dp[N][N];
 int vis[N];
 int d[N];
 vector<int> g[N];

 struct edge
 {
     int to,cost;

     edge(int a,int b)
     {
         to = a;
         cost = b;
     }
 };

 long long prim(int n)
 {
     memset(vis,,sizeof(vis));
     memset(used,,sizeof(used));
     //memset(path,0,sizeof(path));

     for (int i = ;i < n;i++) g[i].clear();

     vis[] = ;
     d[] = ;

     for (int i = ;i < n;i++)
     {
         d[i] = mp[][i];
         pre[i] = ;
     }

     int ans = ;

     for (int i = ;i < n - ;i++)
     {
         int x;
         int dis = inf;

         for (int j = ;j < n;j++)
         {
             if (!vis[j] && d[j] < dis)
             {
                 x = j;
                 dis = d[j];
             }
         }

         vis[x] = ;

         used[x][pre[x]] = used[pre[x]][x] = ;

         g[x].push_back(pre[x]);
         g[pre[x]].push_back(x);

         ans = ans + dis;

         for (int j = ;j < n;j++)
         {
             //if (vis[j] && j != x) path[x][j] = path[j][x] = max(dis,path[j][pre[x]]);

             if (!vis[j] && mp[x][j] < d[j])
             {
                 d[j] = mp[x][j];
                 pre[j] = x;
             }
         }
     }

     return ans;
 }

 int dfs(int root,int u,int fa)
 {
     int s = inf;

     for (int i = ;i < g[u].size();i++)
     {
         int v = g[u][i];

         if (v == fa) continue;

         int tmp = dfs(root,v,u);

         s = min(tmp,s);

         dp[u][v] = dp[v][u] = min(dp[u][v],tmp);
     }

     if (root != fa)
         s = min(s,mp[root][u]);

     return s;
 }

 void solve(int n)
 {
     memset(dp,inf,sizeof(dp));

     for (int i = ;i < n;i++)
     {
         dfs(i,i,-);
     }
 }

 int main()
 {
     int n,m;

     while (scanf("%d%d",&n,&m) != EOF)
     {
         if (m ==  && n == ) break;

         memset(mp,inf,sizeof(mp));

         for (int i = ;i < n;i++)
         {
             g[i].clear();
         }

         for (int i = ;i < m;i++)
         {
             int a,b,c;

             scanf("%d%d%d",&a,&b,&c);

             mp[a][b] = mp[b][a] = c;

             //G[a].push_back(edge(b,c));
             //G[b].push_back(edge(a,c));
         }

         int ans = prim(n);

         solve(n);

         //printf("ans = %d\n",ans);

         int q;

         scanf("%d",&q);

         long long res = ;

         for (int i = ;i < q;i++)
         {
             int x,y,c;

             scanf("%d%d%d",&x,&y,&c);

             if (!used[x][y]) res += ans;
             else
             {
                 long long tmp = (long long)ans + c - mp[x][y];

                 //printf("%d **\n",dp[x][y]);

                 tmp = min(tmp,(long long)ans + dp[x][y] - mp[x][y]);

                 res += tmp;

                 //printf("%d %lld**\n",dp[x][y],tmp);
             }
         }

         printf("%.4f\n",(double) res / q);
     }

     return ;
 }