2019年华南理工大学软件学院ACM集训队选拔赛 Round1

TIps： 1.所有代码中博主使用了scanf和printf作为输入输出 

　　　 2.代码中使用了define LL long long 所以在声明变量的时候 LL其实就等价于long long

希望这两点不会成为读者看代码时候的障碍qwq 另外题目链接我会放在最后 如果需要请往下拖一拖

T1 

这道题其实就是单纯对数据进行排序，但是因为关键字不止一种（解题数m和罚时t） 并且输出的是队伍的名字（也就是序号）

而正常排序完之后我们就会发现 我们并不知道当前各个位置的数对应的队伍名是什么了（也就是其原本的位置信息已经在排序过程中丢失了）

这个时候我们发现 一个队伍有三种信息 解题数 罚时 以及队伍名 我们需要把这三种信息作为一个整体再将这个整体按照内部的信息（解题数以及罚时）进行排序

这个时候我们就需要用到结构体了 也就是这个东西

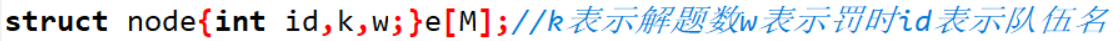
然后利用sort函数将结构体进行排序 但是这里我们需要自定义一个比较函数 按照自己的想法将结构体进行排序 这也就是代码中的cmp函数的作用

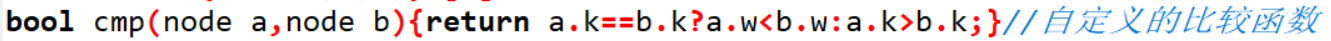
这里用到了三目运算符 不了解的同学可以百度一下他的用法 这里的cmp可以理解为先比较a和b的解题数，解题数多的在前，解题数一样再比较罚时，罚时多的在后

这样之后通过sort函数进行排序再按顺序输出id就可以解决问题了！ 复杂度Ο（nlogn）

贴一下代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
#include<set>
#define LL long long
using namespace std;
const int M=1e5+;
int T,n;
struct node{int id,k,w;}e[M];//k表示解题数w表示罚时id表示队伍名
bool cmp(node a,node b){return a.k==b.k?a.w<b.w:a.k>b.k;}//自定义的比较函数
int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%d",&n);
        for(int i=;i<=n;i++){
            e[i].id=i;
            scanf("%d %d",&e[i].k,&e[i].w);
        }
        sort(e+,e++n,cmp);//排序
        for(int i=;i<=n;i++) printf("%d ",e[i].id); puts("");//puts("")作用只是换行
    }
    return ;
}

 T2

这道题的话 我的做法和题解中的做法一样qwq 师兄讲的也非常清楚 这里就直接引用了

复杂度 Ο（n^2）

贴一下代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
#include<set>
#define LL long long
using namespace std;
const int M=1e6+;
int T,n,l,r;
int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%d",&n);
        puts("YES");
        for(int i=;i<=n;i++){
            for(int j=;j<=n;j++){
                int now=(j-)*n+(i+j-<=n?i+j-:i+j--n);
                printf("%d ",now);
            }
            puts("");
        }
    }
    return ;
}

T3

这道题很明显贪心是不行的 （对于这一题来说，贪心是指我们只考虑是从i层利用电梯到第i+1层，或者单纯走楼梯上去，然后对于每一层把二者取最优解传递给上一层）

因为很显然我们可以一口气坐好几层的电梯QAQ

所以对于每一层i，我们还要记录我们是否还在电梯井内

其实这个问题是典型的动态规划（DP）不懂的同学可以了解一下 这里也给各位提供一下比较好的博客

入门的话一般会先看背包问题 https://blog.csdn.net/weixin_41162823/article/details/87878853

而与这道题类似的DP经典题目 如

导弹拦截 https://www.luogu.com.cn/problem/P1020

最长上升子序列 https://www.luogu.com.cn/problem/P3902

题解的话洛谷都有 不会可以康康

回到这道题本身 我们用ans[i][0],ans[i][1]分别表示到达第i层的最短时间

0表示上一层是坐电梯上来的 也就是这一层要坐电梯的话就不用等待了

1表示上一层是走路上来的 这一层如果要坐电梯就需要等待了

那么我们的转移方程就可以表示为

ans[i][0]=min(ans[i-1][0],ans[i-1][1])+b[i]

ans[i][1]=min(ans[i-1][0]+m,ans[i-1][1])+a[i]

最后输出min(ans[n][0],ans[n][1])问题就解决了qwq

复杂度 O（n）贴一下代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
#include<set>
#define LL long long
using namespace std;
const int M=1e6+;
int T,n,m;
LL a[M],b[M],ans[M][];//0不坐1坐
int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%d %d",&n,&m); n--;
        for(int i=;i<=n;i++) scanf("%lld",&a[i]);
        for(int i=;i<=n;i++) scanf("%lld",&b[i]);
        ans[][]=b[]; ans[][]=a[]+m;
        for(int i=;i<=n;i++){
            ans[i][]=min(ans[i-][],ans[i-][])+b[i];//这一层走路去下一层
            ans[i][]=min(ans[i-][]+m,ans[i-][])+a[i];//这一层坐电梯去下一层
        }
        printf("%lld\n",min(ans[n][],ans[n][]));
    }
    return ;
}

T4

这道题可以理解为利用容斥原理实现吧

首先我们要明确 CAT子序列虽然不用连续 但是相对顺序是不能变的 也就是形如”TAC“是不符合喵喵字符串的定义的

那么我们考虑维护 C[i],A[i],T[i],CA[i],AT[i],CAT[i]六个数组

C[i]表示从1到i一共有几个C字符 A[i],T[i]同理 也就是维护一下前缀和

CA[i]就是维护1到i位置一共有多少种CA的组合 例如一个字符串CCAA 那么CA[4]=4

AT[i],CAT[i]同理

这样之后 对于每一个询问l r

答案 ans=CAT[r]-CAT[l-1]-CA[l-1]*(T[r]-T[l-1])-C[l-1]*(AT[r]-AT[l-1]-A[l-1]*(T[r]-T[l-1]));

CAT[l-1]指的是1到l-1的CAT串 这种位置的串明显是不合法的

CA[l-1]*(T[r]-T[l-1])指的是用 1 到 l-1 的“CA”和 l 到 r 的T组合而成的“CAT” 这也是不合法的子序列

C[l-1]*(AT[r]-AT[l-1]-A[l-1]*(T[r]-T[l-1]))指的是用 1 到 l-1 的“C”和 l 到 r 的“AT”组合而成的CAT 这明显也是不合法的子序列

除去所有的不合法串后我们便可以得到答案了 算法复杂度O（n）

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
#define LL long long
using namespace std;
const int M=2e6+;
int len,m;
LL C[M],A[M],T[M],CA[M],AT[M],CAT[M];
char s[M];
int main(){
    scanf("%d %d",&len,&m);
    scanf("%s",s+);
    for(int i=;i<=len;i++){
        C[i]=C[i-]; A[i]=A[i-]; T[i]=T[i-];
        if(s[i]=='C') C[i]++;
        else if(s[i]=='A') A[i]++;
        else T[i]++;
    }
    for(int i=;i<=len;i++){
        CA[i]=CA[i-]; AT[i]=AT[i-];
        if(s[i]=='A') CA[i]+=C[i];
        if(s[i]=='T') AT[i]+=A[i];
    }
    for(int i=;i<=len;i++){
        CAT[i]=CAT[i-];
        if(s[i]=='T') CAT[i]+=CA[i];
    }
    int l,r;
    for(int i=;i<=m;i++){
        scanf("%d %d",&l,&r);
        LL ans=CAT[r]-CAT[l-]-CA[l-]*(T[r]-T[l-])-C[l-]*(AT[r]-AT[l-]-A[l-]*(T[r]-T[l-]));
        printf("%lld\n",ans);
    }
    return ;
}

T5

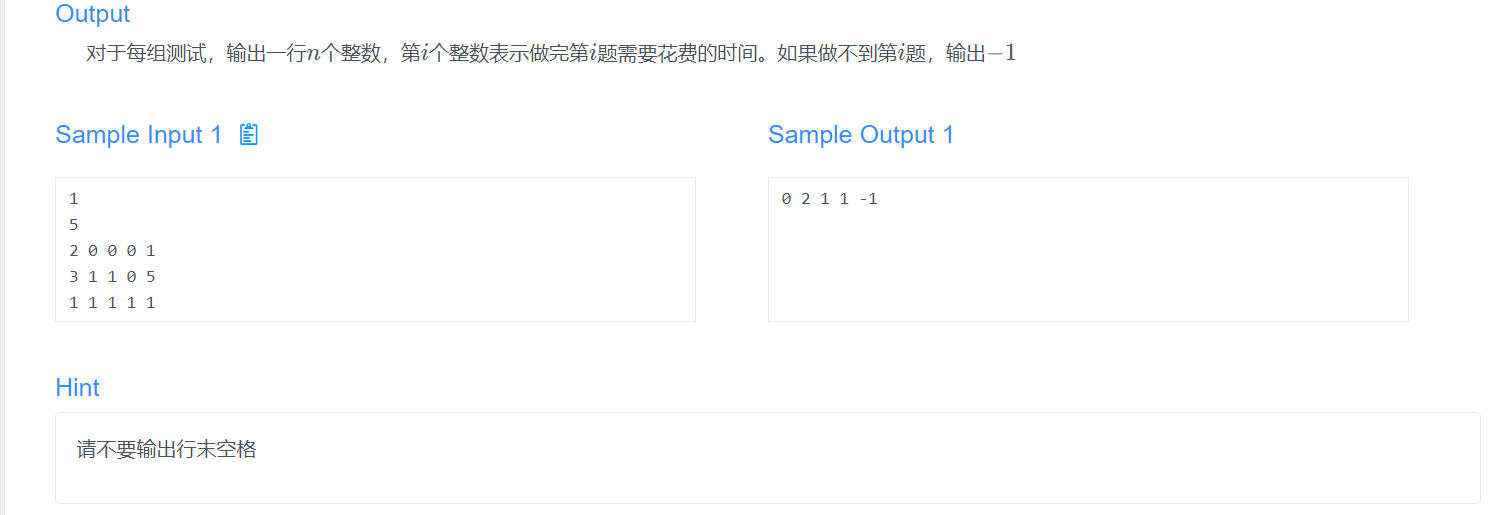
这道题确实算是最难的题目了 大部分同学暂时可以跳过 以后再回来写这道题会容易很多

所以继续往下看的同学我会理解为你是有一定图论基础的

这道题看起来是一道最短路问题 但是我们但我们发现只要每个 l[i] 足够小 r[i] 足够大，那么就可以成为一张完全图 这样无论是dijkstra还是spfa都会超时

我们先按照dijkstra的想法开始解决问题 但是我们发现 因为一点个去到其他任何一个他所能到达的点的距离都是一样的

那么我们将他丢进优先队列的时候 可以将他离1点的距离dis[i]加上他本身的c[i] 一起丢进优先队列中 那么每次从优先队列里拿出来的点就一定是当前所能更新的离1最近的点了

这样一来每个点只需要被更新一次就一定是最优解了 那么我们可以利用set维护当前未被更新的点 如果他被更新就将他从set中删除

这样就可以避免多次访问同一个点 复杂度就降下来了 因为每个点只会被访问到一次 所以复杂度是O（nlogn）

贴一下代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
#include<set>
#include<queue>
#define LL long long
using namespace std;
const int M=2e6+;
LL read(){
    LL ans=,f=,c=getchar();
    while(c<''||c>''){if(c=='-') f=-; c=getchar();}
    while(c>=''&&c<=''){ans=ans*+(c-''); c=getchar();}
    return ans*f;
}
LL T,n,w[M],ans[M],l[M],r[M];
struct node{
    LL id,d;
    bool operator <(const node&x)const{return x.d<d;}
};
priority_queue<node>q;
set<LL>S;
set<LL>::iterator L,R,C;
int main(){
    T=read();
    while(T--){
        while(!q.empty()) q.pop();
        S.clear();
        n=read();
        for(int i=;i<=n;i++) ans[i]=-,S.insert(i);
        for(int i=;i<=n;i++) l[i]=read();
        for(int i=;i<=n;i++) r[i]=read();
        for(int i=;i<=n;i++) w[i]=read();
        ans[]=; q.push((node){,w[]});
        while(!S.empty()&&!q.empty()){
            node x=q.top(); q.pop();
            if(l[x.id]>r[x.id]) continue;
            L=S.lower_bound(x.id+l[x.id]);
            R=S.upper_bound(x.id+r[x.id]);
            while(L!=R){
                ans[*L]=x.d;
                q.push((node){*L,x.d+w[*L]});
                C=S.upper_bound(*L);
                S.erase(L);
                L=C;
            }
            L=S.lower_bound(x.id-r[x.id]);
            R=S.upper_bound(x.id-l[x.id]);
            while(L!=R){
                ans[*L]=x.d;
                q.push((node){*L,x.d+w[*L]});
                C=S.upper_bound(*L);
                S.erase(L);
                L=C;
            }
        }
        for(int i=;i<n;i++) printf("%lld ",ans[i]); printf("%lld",ans[n]); puts("");
    }
    return ;
}

当然对于不会STL的同学 我们也可以考虑利用并查集代替set的作用 也就是每次更新完一个点就将他指向右边的点（与右边的点合并）这样下次再访问到他就可以

直接跳到离他最近的右边的第一个点 同样可以解决多次访问同一个点的问题 当然因为博主比较懒 代码过两天再补上吧qwq

T1 http://110.64.92.203/contest/30/problem/1001

T2 http://110.64.92.203/contest/30/problem/1002

T3 http://110.64.92.203/contest/30/problem/1003

T4 http://110.64.92.203/contest/30/problem/1004

T5 http://110.64.92.203/contest/30/problem/1005