手写BP（反向传播）算法

BP算法为深度学习中参数更新的重要角色，一般基于loss对参数的偏导进行更新。

一些根据均方误差，每层默认激活函数sigmoid（不同激活函数，则更新公式不一样）

假设网络如图所示：

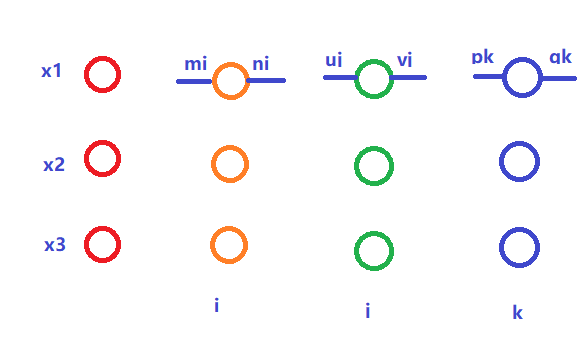
则更新公式为：

以上列举了最后2层的参数更新方式，第一层的更新公式类似，即上一层的误差来自于下一层所有的神经元，e的更新就是不断建立在旧的e上（这里g可以当做初始的e）

下面上代码：

1，BP算法

# 手写BP算法
import numpy as np

# 先更新参数，再继续传播
# layers：包括从输入层到输出层，每层参数为：连接权重w，阈值b，输出y。类型为np.array
# 对于输入层，w和b随便是啥，反正不用，只需y即原始输入
# 基于激活函数sigmoid
# loss为均方误差
def bp(layers,labels,lr=0.001):
#     翻转layers，反向传播
    reversed_layers=layers[::-1]
#     输出层
    output_w,output_b,output_y=reversed_layers[0]
    g=np.array([output_y[j]*(1-output_y[j])*(labels[j]-output_y[j]) for j in range(len(labels))])
#     最后一层更新较为特殊，先进行更新
    delta_w=np.empty(shape=(output_w.shape[0],output_w.shape[1]))
#     上一层输出y
    last_y=reversed_layers[1][2]
    for h in range(output_w.shape[0]):
        for j in range(output_w.shape[1]):
            delta_w[h,j]=lr*g[j]*last_y[h]
    delta_b=-lr*g
    new_w=output_w+delta_w
    new_b=output_b+delta_b
    reversed_layers[0][0]=new_w
    reversed_layers[0][1]=new_b

    #     从倒数第二层到第二层进行更新，每次取3层进行计算，由公式知，需用到上一层输出即下一层权重
    for i in range(1,len(reversed_layers)-1):
#         下一层w
        next_w=reversed_layers[i-1][0]
        out_w,out_b,out_y=reversed_layers[i]
#         上一层y
        last_y=reversed_layers[i+1][2]
#         更新辅助量，意思即上一层每个神经元的误差都由下一层所有神经元的误差反向传播，体现在这里内循环
        e=np.empty(shape=(len(out_b),1))
        for h in range(len(out_b)):
            temp=0
            for j in range(next_w.shape[1]):
                temp+=next_w[h,j]*g[j]
            e[h]=out_y[h]*(1-out_y[h])*temp
        delta_w=np.empty(shape=(out_w.shape[0],out_w.shape[1]))
        for h in range(out_w.shape[0]):
            for j in range(out_w.shape[1]):
                delta_w[h,j]=lr*e[j]*last_y[h]
        delta_b=-lr*e
        out_new_w=out_w+delta_w
        out_new_b=out_b+delta_b
        reversed_layers[i][0]=out_new_w
        reversed_layers[i][1]=out_new_b
        g=np.copy(e)
    return layers

以上假设每个神经元的输出为一个实数y值

2，构建测试

构建平面上的点（x,y），将y是否大于0作为划分，进行训练。只使用了一层网络，sigmoid激活

X=[]
Y=[]
for i in range(-100,100):
    for j in range(-100,100):
        X.append([[i],[j]])
        if j>=0:
            Y.append([1])
        else:
            Y.append([0])
X=np.array(X)
Y=np.array(Y)

3，划分训练，验证集

indexs=np.random.choice(range(40000),size=30000)

x_train=np.array([X[i] for i in indexs])
y_train=np.array([Y[i] for i in indexs])

x_val=np.array([X[i] for i in np.setdiff1d(range(40000),indexs))
y_val=np.array([Y[i] for i in np.setdiff1d(range(40000),indexs))

4，训练。这里只对所有样本训练了一轮。使用随机初始化的w和b，每个样本都会改变w和b

# 使用sigmoid激活函数
def output(input_x,w,b):
    res=0
    t=np.matmul(np.transpose(w),input_x)-b
    return 1./(1+np.power(np.e,-t))

w1=np.random.normal(size=(2,1))
b1=np.array([[0]])
for i in range(len(x_train)):
    y0=x_train[i]
    l=y_train[i]
    input_layers=[]
    w0,b0=(0,0)
    input_layers.append([w0,b0,y0])
    input_layers.append([w1,b1,output(y0,w1,b1)])
    input_layers=bp(input_layers,l)
    w1=input_layers[1][0]
    b1=input_layers[1][1]

# w:  [[0.11213777]
#  [1.67425498]]
# b:  [[0.0001581]]
print('w: ',w1)
print('b: ',b1)

5，验证。从分出的验证集选取部分验证即可

for xx in x_val[:50]:
    print(xx.reshape((2,)),output(xx,w1,b1).reshape((1,)))

验证结果如下：

[63 68] [1.]
[-100  -99] [1.39636722e-77]
[-100  -98] [7.44936654e-77]
[63 69] [1.]
[-100  -96] [2.12011171e-75]
[-100  -94] [6.03390049e-74]
[-100  -93] [3.21897678e-73]
[63 74] [1.]
[-100  -91] [9.16130293e-72]
[63 75] [1.]
[63 76] [1.]
[63 77] [1.]
[63 78] [1.]
[-100  -86] [3.95872874e-68]
[-100  -85] [2.11191018e-67]
[63 79] [1.]
[-100  -83] [6.01055872e-66]
[-100  -82] [3.20652436e-65]
[63 82] [1.]
[-100  -80] [9.12586299e-64]
[-100  -79] [4.86848285e-63]
[63 83] [1.]
[-100  -77] [1.38558459e-61]
[-100  -76] [7.39184317e-61]
[63 89] [1.]
[-100  -74] [2.10374039e-59]
[63 91] [1.]
[-100  -72] [5.98730724e-58]
[-100  -71] [3.19412012e-57]
[-100  -70] [1.70400531e-56]
[-100  -69] [9.09056014e-56]
[-100  -68] [4.84964942e-55]
[-100  -67] [2.58720025e-54]
[-100  -66] [1.38022454e-53]
[63 99] [1.]
[-100  -64] [3.92815978e-52]
[-100  -63] [2.09560219e-51]
[  64 -100] [2.53988133e-70]
[-100  -61] [5.9641457e-50]
[ 64 -97] [3.85631522e-68]
[ 64 -96] [2.05727442e-67]
[-100  -58] [9.05539386e-48]
[ 64 -90] [4.74253371e-63]
[ 64 -89] [2.53005596e-62]
[ 64 -87] [7.20061393e-61]
[-100  -52] [2.08749548e-43]
[ 64 -84] [1.09327301e-58]
[-100  -50] [5.94107377e-42]
[ 95 -13] [1.49260907e-05]
[-100  -45] [2.56722211e-38]

6，总结：可以看出，这50个验证样本上都没问题，虽然想到的测试方案有点low，但一时找不到啥好数据。由此验证BP算法的正确性。如有可疑或不足之处，敬请告知。