hdu_3483A Very Simple Problem(C(m,n)+快速幂矩阵)

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3483

A Very Simple Problem

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 945    Accepted Submission(s): 471

Problem Description

This is a very simple problem. Given three integers N, x, and M, your task is to calculate out the following value:

 

Input

There are several test cases. For each case, there is a line with three integers N, x, and M, where 1 ≤ N, M ≤ 2*10⁹, and 1 ≤ x ≤ 50.
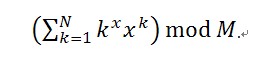
The input ends up with three negative numbers, which should not be processed as a case.

 

Output

For each test case, print a line with an integer indicating the result.

 

Sample Input

100 1 10000
3 4 1000
-1 -1 -1

 

Sample Output

5050
444

 

Source

2010 ACM-ICPC Multi-University Training Contest（5）——Host by BJTU

 

 //计算排列数（杨辉三角）
 //C(m,n) = C(m-1,n-1)+C(m-1,n)
 //快速幂
 /*
 *  [题意]
 *   输入n, x, m
 *   求(1^x)*(x^1)+(2^x)*(x^2)+(3^x)*(x^3)+...+(n^x)*(x^n)
 *  [解题方法]
 *   设f[n] = [x^n, n*(x^n), (n^2)*(x^n),..., (n^x)*(x^n)]
 *   则f[n][k] = (n^k)*(x^n)
 *   问题转化为求：( g[n] = f[1][x]+f[2][x]+...+f[n][x] )
 *   设C(i,j)为组合数，即i种元素取j种的方法数
 *   所以有：f[n+1][k] = ((n+1)^k)*(x^(n+1)) （二次多项式展开）
 *                     = x*( C(k,0)*(x^n)  +C(k,1)*n*(x^n)+...+C(k,k)*(n^k)*(x^n) )
 *                     = x*( C(k,0)*f[n][0]+C(k,1)*f[n][1]+...+C(k,k)*f[n][k] )
 *   所以得：
 *   |x*1 0................................0|        |f[n][0]|       |f[n+1][0]|
 *   |x*1 x*1 0............................0|        |f[n][1]|       |f[n+1][1]|
 *   |x*1 x*2 x*1 0........................0|    *   |f[n][2]|   =   |f[n+1][2]|
 *   |......................................|        |.......|       |.........|
 *   |x*1 x*C(k,1) x*C(k,2)...x*C(k,x) 0...0|        |f[n][k]|       |f[n+1][k]|
 *   |......................................|        |.......|       |.........|
 *   |x*1 x*C(x,1) x*C(x,2).......x*C(x,x) 0|        |f[n][x]|       |f[n+1][x]|
 *   |0................................0 1 1|        |g[n-1] |       | g[ n ]  |
 */
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 #define ll long long
 const ll maxn = ;
 ll c[maxn][maxn];
 ll n, mod, x, m;
 struct Mat{
     ll f[maxn][maxn];
 };
 void init()
 {
     ll i,j,k;
     c[][] = c[][] = c[][] = ;
     for(i = ; i < maxn; i++){
         c[i][] = c[i][i] = ;
         for(j = ; j < i; j++){
             c[i][j] = c[i-][j]+c[i-][j-];
         }
     }
 }
 Mat operator *(Mat a, Mat b)
 {
     ll i, j, k;
     Mat c;
     memset(c.f,,sizeof(c.f));
     for(k = ; k < m; k++){
         for(i = ; i < m; i++){
             for(j = ; j < m; j++){
                 if(!b.f[k][j]) continue;
                 c.f[i][j] = (c.f[i][j]+(a.f[i][k]*b.f[k][j])%mod)%mod;
             }
         }
     }
     return c;
 }
 Mat multi(Mat a,ll b)
 {
     Mat s;
     memset(s.f,,sizeof(s.f));
     for(int i = ; i < m; i++){
         s.f[i][i] = ;
     }
     while(b){
         if(b&) s = s*a;
         a = a*a;
         b>>=;
     }
     return s;
 }
 int main()
 {
     init();
     while(~scanf("%lld%lld%lld",&n,&x,&mod))
     {
         if(n<&&x<&&mod<) break;
         Mat e;
         ll i, j;
         ll ans = ;
         memset(e.f,,sizeof(e.f));
         for(i = ; i <= x; i++){
             for(j = i; j <= x; j++){
                 e.f[j][i] = c[x-i][j-i]*x%mod;
             }
         }
         e.f[][x+] = e.f[x+][x+] = ;
         m = x+;
         e = multi(e,n);
         for(i = ; i < m-; i++) ans = (ans+x*e.f[i][m-])%mod;
         printf("%lld\n",(ans+mod)%mod);
     }
     return ;
 }