堆优化dijstra
因为spfa没事就被卡一卡,所以堆优化dijstra就显得很重要,在最短路或者其模型里边,最少有一条边是没有被更新过的,也就是它是最短的,同理从这个点开始也有一条边最短,所以每次就找最短的然后松弛操作就可以的。
#include<iostream>
#include<cstdio>
#include<queue>
#include<algorithm>
#include<cmath>
#include<ctime>
#include<set>
#include<map>
#include<stack>
#include<cstring>
#define inf 2147483647
#define ls rt<<1
#define rs rt<<1|1
#define lson ls,nl,mid,l,r
#define rson rs,mid+1,nr,l,r
#define N 200010
#define For(i,a,b) for(register long long i=a;i<=b;i++)
#define p(a) putchar(a)
#define g() getchar() using namespace std;
long long n,m,s;
long long x,y,v;
bool vis[N]; struct node{
long long n;
long long v;
node *next;
}*e[N]; struct Node
{
long long i;
long long d;
bool operator < (const Node&temp)const{
return d>temp.d;
}
}a[N]; priority_queue<Node>q; void in(long long &x){
long long y=;
char c=g();x=;
while(c<''||c>''){
if(c=='-')y=-;
c=g();
}
while(c<=''&&c>=''){
x=(x<<)+(x<<)+c-'';c=g();
}
x*=y;
}
void o(long long x){
if(x<){
p('-');
x=-x;
}
if(x>)o(x/);
p(x%+'');
} void push(long long x,long long y,long long v){
node *p;
p=new node();
p->n=y;
p->v=v;
if(e[x]==NULL)
e[x]=p;
else{
p->next=e[x]->next;
e[x]->next=p;
}
} void hd(){
a[s].d=;
q.push(a[s]);
while(!q.empty()){
long long t=q.top().i;
q.pop();
if(vis[t])continue;
vis[t]=true;
for(register node *i=e[t];i;i=i->next){
if(a[t].d+i->v<a[i->n].d){
a[i->n].d=a[t].d+i->v;
q.push(a[i->n]);
}
}
}
} int main(){
in(n);in(m);in(s); For(i,,m){
in(x);in(y);in(v);
push(x,y,v);
} For(i,,n){
a[i].i=i;
a[i].d=inf;
}
hd();
For(i,,n){
o(a[i].d);
p(' ');
}
return ;
}
!!!!!
它不能处理有负权边,也不能处理最长路!!!!
要牢记啊233333
比如求这个1到2的最短路
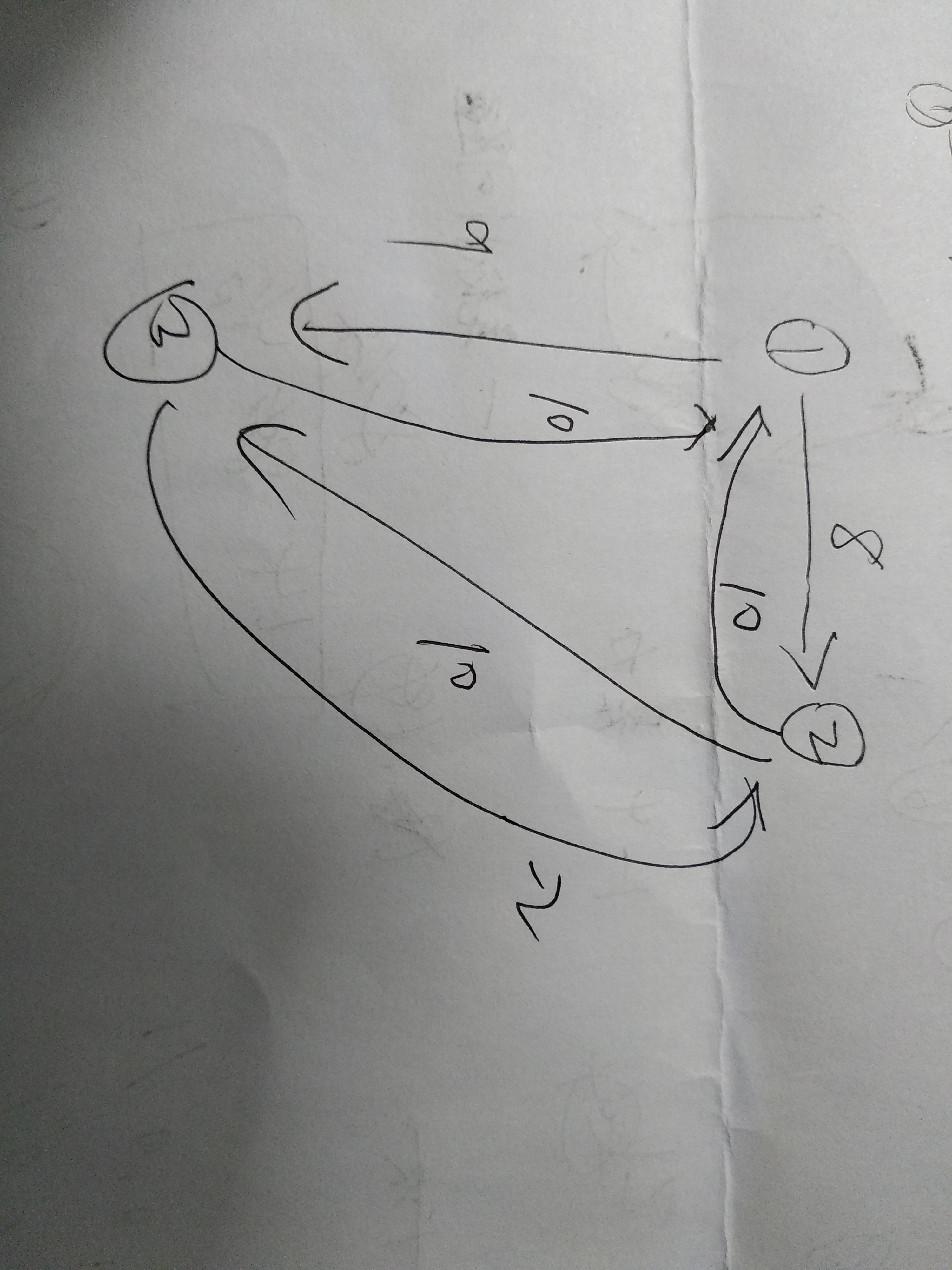
堆优化dijstra的更多相关文章
- HDU-6290_奢侈的旅行(Dijstra+堆优化)
奢侈的旅行 Time Limit: 14000/7000 MS (Java/Others) Memory Limit: 512000/512000 K (Java/Others) Problem De ...
- 【Dijstra堆优化】HDU 3986 Harry Potter and the Final Battle
http://acm.hdu.edu.cn/showproblem.php?pid=3986 [题意] 给定一个有重边的无向图,T=20,n<=1000,m<=5000 删去一条边,使得1 ...
- 最短路-朴素版Dijkstra算法&堆优化版的Dijkstra
朴素版Dijkstra 目标 找到从一个点到其他点的最短距离 思路 ①初始化距离dist数组,将起点dist距离设为0,其他点的距离设为无穷(就是很大的值) ②for循环遍历n次,每层循环里找出不在S ...
- Dijkstra和堆优化
Dijkstra算法 由于我之前一直记的迪杰斯特拉的翻译导致我把dijkstra写成了dijstra--所以下文#define dijstra dijkstra 我以后叫她迪杰克斯歘! Dijskra ...
- uva10986 堆优化单源最短路径(pas)
var n,m,s,t,v,i,a,b,c:longint;//这道题的代码不是这个,在下面 first,tr,p,q:..]of longint; next,eb,ew:..]of longint; ...
- 最短路模板(Dijkstra & Dijkstra算法+堆优化 & bellman_ford & 单源最短路SPFA)
关于几个的区别和联系:http://www.cnblogs.com/zswbky/p/5432353.html d.每组的第一行是三个整数T,S和D,表示有T条路,和草儿家相邻的城市的有S个(草儿家到 ...
- 堆优化的Dijkstra
SPFA在求最短路时不是万能的.在稠密图时用堆优化的dijkstra更加高效: typedef pair<int,int> pii; priority_queue<pii, vect ...
- codeforces 449B Jzzhu and Cities (Dij+堆优化)
输入一个无向图<V,E> V<=1e5, E<=3e5 现在另外给k条边(u=1,v=s[k],w=y[k]) 问在不影响从结点1出发到所有结点的最短路的前提下,最多可以 ...
- POJ 1511 - Invitation Cards 邻接表 Dijkstra堆优化
昨天的题太水了,堆优化跑的不爽,今天换了一个题,1000000个点,1000000条边= = 试一试邻接表 写的过程中遇到了一些问题,由于习惯于把数据结构封装在 struct 里,结果 int [10 ...
随机推荐
- NPOI写Excel,Microsoft.Office.Interop.excel.dll 转换Excel为PDF
首先要引用NPOI动态库和Microsoft.Office.Interop.excel.dll (Microsoft.Office.Interop.excel.dll 下载链接 ,下载以后解压文件,把 ...
- OCM 学习练习题目
1:数据安装操作练习:考试题目 1: Creating a database & Server Configuration --[101]-- #创建数据库 1. Create the dat ...
- 后RCNN时代的物体检测及实例分割进展
https://mp.weixin.qq.com/s?__biz=MzA3MzI4MjgzMw==&mid=2650736740&idx=3&sn=cdce446703e69b ...
- MYSQL查询系列 常考问题
表结构: `student`('id'.'name'.'code'.'age'.'sex')学生表 `teacher`('id'.'name')教师表 `course`('id'.'name'.'te ...
- ajax执行成功后,在success回调函数中把后台返回的list还原到html的table中
需求描述:前台通过onclick触发ajax,到后台返回一个list(json格式的),把list插入到html的table中. 思路简介: ̄□ ̄|| 刚开始的时候,是没有思路的,就卡在了,怎么把 a ...
- 高斯消元处理无解|多解情况 poj1830
高斯消元结束后,若存在系数为0,常数不为0的行,则方程无解 若系数不为0的行有k个,则说明主元有k个,自由元有n-k个,方程多解 /* 给定n个开关的初始状态si,要求将其变成目标状态di 规定: 每 ...
- Axure之全局变量
****全局变量*****1.定义:变量是一个数据的容器,是一个字符串,可设置默认值:2.功能:两个功能:读.写3.特点:随时随地可以对变量进行读和写,不限页面.也就是在不同的页面也可以访问同一个全局 ...
- delete web server(nginx)
#!/bin/bash conf_dir1="/usr/local/nginx/conf/vhost.d" #conf_dir2="/usr/local/apache2/ ...
- C# 不使用递归遍历目录树中的文件和文件夹
public class StackBasedIteration { static void Main(string[] args) { // Specify the starting folder ...
- requests禁止重定向
response = requests.get( 'http://weixin.sogou.com/weixin?query=%E9%A3%8E%E6%99%AF&type=2&pag ...
