p68理想的性质
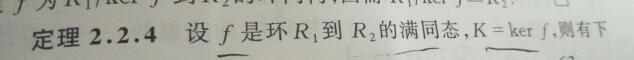
1.如何由2.2.4推出后面的结论?
2.为什么A可以等于R？
3.如何证明3？
- π：R->R/M套用定理2.2.4（2）和（1）
R2是R/M，I是R/M的理想也就是R2的理想，所以f^(-1)I 就能在R1找到一个理想，设为A。使得 I=π（a） I=A/M。M是极大理想，
2.没有真包含极大理想的真理想（不是R的理想），所以A只能是R或M，因为I=A/M,所以I等于或者R/M, R本身是自己的理想。
3.由2.2.4（2）推出2.3.5中的R的理想A对应的π（A）=A/M是R/M,的理想，
域的理想就是0和他自己，所以A/M等于0或者R/M
p68理想的性质的更多相关文章
- 复习交换代数——Noether正规化
目录 简介 初等启发 证明过程 几何意义 定理应用 参考资料 简介 在交换代数中有如下定理 Noether正规化引理 令$R$是一个有限生成$k$-代数整环,则存在$t_1,\ldots,t_n\in ...
- attention 汇总（持续）
Seq2seq Attention Normal Attention 1. 在decoder端,encoder state要进行一个线性变换,得到r1,可以用全连接,可以用conv,取决于自己,这里 ...
- 《A First Course in Probability》-chaper7-期望的性质-期望的性质-协方差
在实际的问题中,我们往往想要通过已有的数据来分析判断两个事件的发生是否有相关性.当然一个角度去寻找这两个事件内在的逻辑关系,这个角度需要深究两个事件的本质,而另外一个角度就是概率论提供的简单方法:基于 ...
- manifold 微分流形上可以定义可微函数、切向量、切向量场、各种张量场等对象并建立其上的分析学，并可以赋予更复杂的几何结构以研究它们的性质。
小结: 1.流形(英语:Manifolds)一般可以通过把许多平直的片折弯并粘连而成,是局部具有欧几里得空间性质的空间,是欧几里得空间中的曲线.曲面等概念的推广 2.描述一个流形往往需要不止一个“地图 ...
- 【黑金原创教程】【Modelsim】【第三章】理想就是美丽
声明:本文为黑金动力社区(http://www.heijin.org)原创教程,如需转载请注明出处,谢谢! 黑金动力社区2013年原创教程连载计划: http://www.cnblogs.com/al ...
- Solid Edge性质管理者 如何获取装配体的BOM表 物料清单
工具-性质管理者 在里面可以输入每个文件的文件号,版本号,作者等信息 右击点击显示性质,你还可以添加或删除文件属性 把需要的属性更改好了之后,可以输出装配体的所有零件信息到Excel中,点击工 ...
- B样条基函数的定义和性质
定义:令U={u0,u1,…,um}是一个单调不减的实数序列,即ui≤ui+1,i=0,1,…,m-1.其中,ui称为节点,U称为节点矢量,用Ni,p(u)表示第i个p次(p+1阶)B样条基函数,其定 ...
- Anders Hejlsberg 技术理想架构开发传奇
Anders Hejlsberg(安德斯-海森博格) 坐在自己的办公室,双眼直直的盯着前方.他要做一个决定,决定自己未来的命运和理想.这是1996年一个普通的下午,几个小时前,他刚与比尔-盖茨结束了 ...
- BZOJ1047: [HAOI2007]理想的正方形 [单调队列]
1047: [HAOI2007]理想的正方形 Time Limit: 10 Sec Memory Limit: 162 MBSubmit: 2857 Solved: 1560[Submit][St ...
随机推荐
- 深入理解C语言内存管理
之前在学Java的时候对于Java虚拟机中的内存分布有一定的了解,但是最近在看一些C,发现居然自己对于C语言的内存分配了解的太少. 问题不能拖,我这就来学习一下吧,争取一次搞定. 在任何程序设计环境及 ...
- Linux-Centos7系统下安装python2并与python3版本共存
问题描述: 最近有个需求是想在centos下安装python3.5 因为django这边用到是这个版本 1.查看系统版本和python版本 Centos7.6版本默认安装的是python2.7.5版本 ...
- LeetCode算法题-First Bad Version（Java实现-三种解法）
这是悦乐书的第200次更新,第210篇原创 01 看题和准备 今天介绍的是LeetCode算法题中Easy级别的第66题(顺位题号是278).您是产品经理,目前领导团队开发新产品.不幸的是,您产品的最 ...
- LeetCode算法题-Reverse Linked List（Java实现）
这是悦乐书的第192次更新,第195篇原创 01 看题和准备 今天介绍的是LeetCode算法题中Easy级别的第51题(顺位题号是206).反转单链表.例如: 输入:1-> 2-> 3- ...
- LeetCode算法题-Count Primes（Java实现）
这是悦乐书的第190次更新,第193篇原创 01 看题和准备 今天介绍的是LeetCode算法题中Easy级别的第49题(顺位题号是204).计算小于非负数n的素数的数量.例如: 输入:10 输出:4 ...
- CORS(跨域资源共享)详解及与JSONP的对比
上篇讲解的JSONP的跨域请求方式,但是在浏览器的支持及请求方式上有局限性,接下来将介绍一种新的跨域请求方式CORS. CORS是一个W3C标准,全称是"跨域资源共享"(Cross ...
- nodejs前后分离
proxy: { '/api': { target: 'http://localhost:3000/', pathRewrite: {'^/api' : ''}, changeOrigin: true ...
- centos7下安装docker（26如何配置Health Check）
Docker只能从容器启动进程的返回代码判断其状态,而对于容器内部应用的运行状况基本没有了解 执行docker run命令时,通常根据dockerfile中的CMD或ENTRYPOINT启动一个进程, ...
- 复制数据库的Shell命令
mysqldump -h$host db_old -uroot -p$pass | mysql -h$host db_new -uroot -p$pass 管道符号,是unix一个很强大的功能,符号为 ...
- 小a的轰炸游戏 （差分）
我是看题解的! 这道题还是有很多细节,当然,是一道差分的好题! 题意:有2种飞机,一种是只炸上半菱形,一种是炸整个菱形.问所有区域内的所有格子的异或和. 思路:用前缀和思路: 这样遍历过去就完成了一次 ...