HGOI 20190407 Typing Competition Round #1 出题记
/*
ljc20020730出的HGOI20190407的模拟赛。
考试结果比预期难的不少，可能是由于本来计划5h的比赛打了4h吧。
就当普及组模拟赛好了...
难度大概4紫吧(弱省省选难度)
出境 小F 命题ljc20020730
*/
杭高互测比赛，这次轮到我出题。
题目是Typing Competition Round #1
出题人是ljc20020730(捂脸)
这是第一次出题，就出了一些毒瘤题目，下次一定会改进的2333!!!
(虽说Task2会有一点点小锅...，但比起某Task3都没STD的模拟赛来说还是良心了不少)
下面将以出题人的角度评析这场比赛，如果有不足还请dalao多多指教。
题目概括：
求树上每个点的最长链$D_i$，m组询问，对于连续区间$[l,r]\subseteq [1,n]$
需满足$Max_{i=l}^{r} D_i - Max_{i=l}^{r} D_i \leq Q$
最大化$r-l+1$的值。
Sol ： 事实上，这道题目出在Task1并不合适，并不小清新。
首先需要特判第一个点，就是没有乡村的时候特判输出0否则会输出1
其次，对于$ O(n) $求全局最长链可以做Dp，设f[u][0]为子树最长链，f[u][1]为子树次长链
设f[u][2]为从父亲转移过来的最长链，考虑儿子更新父亲（显然f[u][0],f[u][1]可以dfs求出）
$ f[u][2]=Dist\{u,v\}+Max(f[u][1],f[u][2]) $[v 是 u最长链经过的点]
$ f[u][2]=Dist\{u,v\}+Max(f[u][0],f[u][2])$ [v 非 u最长链经过的点]
然后对于每个点$D_i = Max(f[i][2],f[i][0])$ 即可
对于部分链的点貌似需要手打栈，其实只需要把根换成$\frac{n}{2}$即可通过
通过计算时间复杂度发现对于区间Max值需要O(1)（由于有nm次询问） 所以打了ST表维护就行
使用类似于单调队列的方法可以做到询问复杂度$O(nm)$
总时间复杂度为$O(n +n log_2 n + nm)$，足以通过所有数据。
# include <cstring>
# include <cstdio>
# include <cmath>
# define fp(i,s,t) for(int i=s;i<=t;i++)
using namespace std;
const int N=+;
const int Bit=;
struct rec{
int pre,to,w;
}a[N<<];
int cmin[N][],cmax[N][],mark[N],g[N],f[N][],lg2[N];
bool vis[N];
int tot,head[N];
int n,m,root;
inline int max(int a,int b){return (a>b)?a:b;}
inline int min(int a,int b){return (a>b)?b:a;}
inline int read()
{
int X=,w=; char c=;
while(c<''||c>'') {w|=c=='-';c=getchar();}
while(c>=''&&c<='') X=(X<<)+(X<<)+(c^),c=getchar();
return w?-X:X;
}
inline void write(int x)
{
if (x>) write(x/);
putchar(''+x%);
}
inline void adde(int u,int v,int w)
{
a[++tot].pre=head[u];
a[tot].to=v;
a[tot].w=w;
head[u]=tot;
}
void dfs1(int u)
{
vis[u]=;
for (int i=head[u];i;i=a[i].pre){
int v=a[i].to; if (vis[v]) continue;
dfs1(v);
if (f[v][]+a[i].w>f[u][]) {
mark[u]=v;
f[u][]=f[u][];
f[u][]=f[v][]+a[i].w;
} else if (f[v][]+a[i].w>f[u][]) {
f[u][]=f[v][]+a[i].w;
}
}
}
void dfs2(int u)
{
vis[u]=;
for (int i=head[u];i;i=a[i].pre){
int v=a[i].to; if (vis[v]) continue;
if (mark[u]==v) f[v][]=a[i].w+max(f[u][],f[u][]);
else f[v][]=a[i].w+max(f[u][],f[u][]);
dfs2(v);
}
}
void buildRMQ()
{
memset(cmin,0x3f,sizeof(cmin));
for (int i=;i<=n;i++) cmax[i][]=cmin[i][]=g[i];
for (int i=;(<<i)<=n;i++) fp(j,,n)
cmax[j][i]=max(cmax[j][i-],cmax[j+(<<(i-))][i-]),
cmin[j][i]=min(cmin[j][i-],cmin[j+(<<(i-))][i-]);
}
int query(int l,int r)
{
int k=lg2[r-l+];
return max(cmax[l][k],cmax[r-(<<k)+][k])-min(cmin[l][k],cmin[r-(<<k)+][k]);
}
int main()
{
freopen("travel.in","r",stdin);
freopen("travel.out","w",stdout);
n=read();m=read(); root=n>>;
if (n==) {
fp(i,,m) printf("0\n");
return ;
}
fp(i,,n) lg2[i]=log2(i);
fp(i,,n-) {
int u=read(),v=read(),w=read();
adde(u,v,w); adde(v,u,w);
}
dfs1(root);
memset(vis,false,sizeof(vis));
dfs2(root);
fp(i,,n) g[i]=max(f[i][],f[i][]);
buildRMQ();
while (m--) {
int q=read(),l=,ans=;
for (int i=;i<=n;i++) {
while (l<i&&query(l,i)>q) l++;
ans=max(i-l+,ans);
}
write(ans); putchar('\n');
}
return ;
}
travel.cpp
考试时最高分96分原因是没有特判第一个点...
题目概括：
对于一个RP++语言要求支持
for i = p to q
a = b + c
if a = b then(所有格式严格只会出现$a,b,c$三个字母)
Sol ： 细节题目：只需要模拟就可以过75分。
事实上我们会发现多数for循环是没有意义的，分三类讨论即可
1. 赋值 a = b + c套循环
2.累加 a = a + b 套循环
3.乘2 a=a+a套循环
所以可以O(1)处理上面操作。
而对于if 套for 直接拆成if + for按照上面处理即可
而对于for 套 if的情况会发现要么处理对if条件没有影响，此时只需要把if 套在for 外面就行 按照上面处理
要么处理对if条件有影响，但由于a,b,c是大于等于1的所以必然只影响一次，所以直接把for拆掉做if 即可(此处需要判断for 的成立性)
注意处理for循环的时候的倒序循环不需要做处理就行，复杂度可以做到O(length)
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#define int unsigned long long
#define ull unsigned long long
using namespace std;
struct rec {
int opt;
string a1, a2, a3;
} t[];
ull a, b, c;
int n;
string s[];
bool pdc(char x) {
if (x == 'a' || x == 'b' || x == 'c')
return ;
else
return ;
}
ull val(char x) {
if (x == 'a')
return a;
else if (x == 'b')
return b;
else if (x == 'c')
return c;
}
ull pow(ull x, int n) {
ull ans = ;
while (n) {
if (n & )
ans = ans * x;
n >>= ;
x = x * x;
}
return ans;
}
inline void give(char ch1, char ch2, char ch3) {
if (ch1 == 'a' && ch2 == 'a' && ch3 == 'a')
a = a + a;
else if (ch1 == 'a' && ch2 == 'a' && ch3 == 'b')
a = a + b;
else if (ch1 == 'a' && ch2 == 'a' && ch3 == 'c')
a = a + c;
else if (ch1 == 'a' && ch2 == 'b' && ch3 == 'a')
a = b + a;
else if (ch1 == 'a' && ch2 == 'b' && ch3 == 'b')
a = b + b;
else if (ch1 == 'a' && ch2 == 'b' && ch3 == 'c')
a = b + c;
else if (ch1 == 'a' && ch2 == 'c' && ch3 == 'a')
a = c + a;
else if (ch1 == 'a' && ch2 == 'c' && ch3 == 'b')
a = c + b;
else if (ch1 == 'a' && ch2 == 'c' && ch3 == 'c')
a = c + c;
else if (ch1 == 'b' && ch2 == 'a' && ch3 == 'a')
b = a + a;
else if (ch1 == 'b' && ch2 == 'a' && ch3 == 'b')
b = a + b;
else if (ch1 == 'b' && ch2 == 'a' && ch3 == 'c')
b = a + c;
else if (ch1 == 'b' && ch2 == 'b' && ch3 == 'a')
b = b + a;
else if (ch1 == 'b' && ch2 == 'b' && ch3 == 'b')
b = b + b;
else if (ch1 == 'b' && ch2 == 'b' && ch3 == 'c')
b = b + c;
else if (ch1 == 'b' && ch2 == 'c' && ch3 == 'a')
b = c + a;
else if (ch1 == 'b' && ch2 == 'c' && ch3 == 'b')
b = c + b;
else if (ch1 == 'b' && ch2 == 'c' && ch3 == 'c')
b = c + c;
else if (ch1 == 'c' && ch2 == 'a' && ch3 == 'a')
c = a + a;
else if (ch1 == 'c' && ch2 == 'a' && ch3 == 'b')
c = a + b;
else if (ch1 == 'c' && ch2 == 'a' && ch3 == 'c')
c = a + c;
else if (ch1 == 'c' && ch2 == 'b' && ch3 == 'a')
c = b + a;
else if (ch1 == 'c' && ch2 == 'b' && ch3 == 'b')
c = b + b;
else if (ch1 == 'c' && ch2 == 'b' && ch3 == 'c')
c = b + c;
else if (ch1 == 'c' && ch2 == 'c' && ch3 == 'a')
c = c + a;
else if (ch1 == 'c' && ch2 == 'c' && ch3 == 'b')
c = c + b;
else if (ch1 == 'c' && ch2 == 'c' && ch3 == 'c')
c = c + c;
}
inline void workf(char ch1, char ch2, int k) {
if (ch1 == 'a' && ch2 == 'a')
a = a * pow(, k);
else if (ch1 == 'a' && ch2 == 'b')
a = a + k * b;
else if (ch1 == 'a' && ch2 == 'c')
a = a + k * c;
else if (ch1 == 'b' && ch2 == 'a')
b = b + k * a;
else if (ch1 == 'b' && ch2 == 'b')
b = b * pow(, k);
else if (ch1 == 'b' && ch2 == 'c')
b = b + k * c;
else if (ch1 == 'c' && ch2 == 'a')
c = c + k * a;
else if (ch1 == 'c' && ch2 == 'b')
c = c + k * b;
else if (ch1 == 'c' && ch2 == 'c')
c = c * pow(, k);
}
string aa1;
bool fun1() {
string a = aa1;
int i, len = a.length();
for (i = ; i < len; i++)
if (pdc(a[i]))
break;
char c1 = a[i];
for (i = i + ; i < len; i++)
if (pdc(a[i]))
break;
char c2 = a[i];
return val(c1) == val(c2);
}
string aa2;
int fun2() {
string a = aa2;
int l = , r = , i, len = a.length();
for (i = ; i < len; i++)
if (a[i] >= '' && a[i] <= '')
break;
for (; i < len; i++)
if (a[i] >= '' && a[i] <= '')
l = (int)l * + a[i] - '';
else
break;
for (i = i + ; i < len; i++)
if (a[i] >= '' && a[i] <= '')
break;
for (; i < len; i++)
if (a[i] >= '' && a[i] <= '')
r = (int)r * + a[i] - '';
else
break;
int zero = ;
if (l < r)
return r - l + ;
else
return ;
}
bool relation() {
int i, len = aa1.length();
for (i = ; i < len; i++)
if (pdc(aa1[i]))
break;
char c1 = aa1[i];
for (i = i + ; i < len; i++)
if (pdc(aa1[i]))
break;
char c2 = aa1[i];
len = aa2.length();
for (i = ; i < len; i++)
if (pdc(aa2[i]))
break;
char c3 = aa2[i];
if (c1 == c3 || c2 == c3)
return ;
else
return ;
}
void work1(int id) {
aa1 = t[id].a1;
if (!fun1())
return;
string a = t[id].a2;
int i, len = a.length();
for (i = ; i < len; i++)
if (pdc(a[i]))
break;
char c1 = a[i];
for (i = i + ; i < len; i++)
if (pdc(a[i]))
break;
char c2 = a[i];
for (i = i + ; i < len; i++)
if (pdc(a[i]))
break;
char c3 = a[i];
give(c1, c2, c3);
}
void work2(int id) {
aa2 = t[id].a1;
int times = fun2();
if (times<=) return;
string a = t[id].a2;
int i, len = a.length();
for (i = ; i < len; i++)
if (pdc(a[i]))
break;
char c1 = a[i];
for (i = i + ; i < len; i++)
if (pdc(a[i]))
break;
char c2 = a[i];
for (i = i + ; i < len; i++)
if (pdc(a[i]))
break;
char c3 = a[i];
if (c2 == c1)
workf(c1, c3, times);
else if (c3 == c1)
workf(c1, c2, times);
else
give(c1, c2, c3);
}
void work0(int id) {
aa1 = t[id].a1;
if (!fun1())
return;
t[id].a1 = t[id].a2;
t[id].a2 = t[id].a3;
work2(id);
}
void work3(int id) {
string a = t[id].a1;
int i, len = a.length();
for (i = ; i < len; i++)
if (pdc(a[i]))
break;
char c1 = a[i];
for (i = i + ; i < len; i++)
if (pdc(a[i]))
break;
char c2 = a[i];
for (i = i + ; i < len; i++)
if (pdc(a[i]))
break;
char c3 = a[i];
give(c1, c2, c3);
}
signed main() {
cin >> a >> b >> c >> n;
getchar();
for (int i = ; i <= n; i++) getline(cin, s[i]);
int i = , cnt = ;
while (i <= n) {
if (s[i][] == 'f') {
if (pdc(s[i + ][])) {
aa2=s[i]; if (fun2()<=) {i+=; continue; }
t[++cnt] = (rec){ , s[i], s[i + ] };
i += ;
} else {
aa2=s[i]; if (fun2()<=) { i+=; continue; }
aa1 = s[i + ]; aa2 = s[i + ];
if (relation()) {
t[++cnt] = (rec){ , s[i + ], s[i + ] };
} else {
t[++cnt] = (rec){ , s[i + ], s[i], s[i + ] };
}
i += ;
}
} else if (s[i][] == 'i') {
if (pdc(s[i + ][])) {
t[++cnt] = (rec){ , s[i], s[i + ] };
i += ;
} else {
aa2=s[i+]; if (fun2()<=) {i+=; continue; }
t[++cnt] = (rec){ , s[i], s[i + ], s[i + ] };
i += ;
}
} else {
t[++cnt] = (rec){ , s[i] };
i++;
}
}
n = cnt;
for (int i = ; i <= n; i++) {
if (t[i].opt == )
work0(i);
else if (t[i].opt == )
work1(i);
else if (t[i].opt == )
work2(i);
else
work3(i);
}
cout << a << " " << b << " " << c << '\n';
return ;
}
language.cpp
考场上最高分是65分，原因是没有处理好一些细节和for循环的优化。
考试时应该是最不可做的题目，为了卡一些选手的时间才放的这道题。
所以遇到毒瘤的模拟题数个0 0 0得分可能比一些选手的分高（心态不能崩!!!）
Sol：概括题目显然非常不必要，这道题应该能一眼看出来是线段树+树链剖分的题目。
树链剖分不必多说，考虑线段树维护的信息。
显然，区间平均值直接维护区间和即可，但是方差并不能直接维护。
经过推倒我们可以发现
显然只需要维护一个区间平方和即可，所以当维护一个区间+d的时候
套树剖以后复杂度是$O(n log_2 ^2 n)$
# include <bits/stdc++.h>
# define Eps (1e-)
using namespace std;
const int N=1e5+;
struct node{
int l,r;
double sum,sqr,add;
}t[N<<];
int n,m;
inline int read()
{
int X=,w=; char c=;
while(c<''||c>'') {w|=c=='-';c=getchar();}
while(c>=''&&c<='') X=(X<<)+(X<<)+(c^),c=getchar();
return w?-X:X;
}
double val[N],tmp[N];
struct rec{
int pre,to;
}a[N<<];
int head[N],tot,cntw,top[N];
int size[N],fa[N],w[N],old[N],dep[N],son[N];
void adde(int u,int v)
{
a[++tot].pre=head[u];
a[tot].to=v;
head[u]=tot;
}
# define ls (x<<)
# define rs ((x<<)+)
void build(int x,int l,int r)
{
t[x].l=l; t[x].r=r;
if (l==r) {
t[x].sum=val[l];
t[x].sqr=val[l]*val[l];
return;
}
int mid=l+r>>;
build(ls,l,mid);
build(rs,mid+,r);
t[x].sum=t[ls].sum+t[rs].sum;
t[x].sqr=t[ls].sqr+t[rs].sqr;
}
void down(int x)
{
if (fabs(t[x].add)<=Eps) return;
double tag=t[x].add; t[x].add=0.0;
t[ls].sqr=t[ls].sqr+*tag*t[ls].sum+1.0*(t[ls].r-t[ls].l+)*tag*tag;
t[rs].sqr=t[rs].sqr+*tag*t[rs].sum+1.0*(t[rs].r-t[rs].l+)*tag*tag;
t[ls].sum=t[ls].sum+1.0*(t[ls].r-t[ls].l+)*tag;
t[rs].sum=t[rs].sum+1.0*(t[rs].r-t[rs].l+)*tag;
t[ls].add=t[ls].add+tag;
t[rs].add=t[rs].add+tag;
}
void modify(int x,int pos,double d)
{
if (t[x].l==t[x].r) {
t[x].sum=d;
t[x].sqr=d*d;
return;
}
down(x);
int mid=(t[x].l+t[x].r)>>;
if (pos<=mid) modify(ls,pos,d);
else modify(rs,pos,d);
t[x].sum=t[ls].sum+t[rs].sum;
t[x].sqr=t[ls].sqr+t[rs].sqr;
}
void update(int x,int opl,int opr,double d)
{
if (opl<=t[x].l&&t[x].r<=opr) {
t[x].sqr=t[x].sqr+*(t[x].sum)*d+1.0*(t[x].r-t[x].l+)*d*d;
t[x].sum=t[x].sum+1.0*(t[x].r-t[x].l+)*d;
t[x].add=t[x].add+d;
return;
}
down(x);
int mid=(t[x].l+t[x].r)>>;
if (opl<=mid) update(ls,opl,opr,d);
if (opr>mid) update(rs,opl,opr,d);
t[x].sum=t[ls].sum+t[rs].sum;
t[x].sqr=t[ls].sqr+t[rs].sqr;
}
double query_sum(int x,int opl,int opr)
{
if (opl<=t[x].l&&t[x].r<=opr) return t[x].sum;
down(x);
int mid=(t[x].l+t[x].r)>>;
double ret=0.0;
if (opl<=mid) ret=ret+query_sum(ls,opl,opr);
if (opr>mid) ret=ret+query_sum(rs,opl,opr);
return ret;
}
double query_sqr(int x,int opl,int opr)
{
if (opl<=t[x].l&&t[x].r<=opr) return t[x].sqr;
down(x);
int mid=(t[x].l+t[x].r)>>;
double ret=0.0;
if (opl<=mid) ret=ret+query_sqr(ls,opl,opr);
if (opr>mid) ret=ret+query_sqr(rs,opl,opr);
return ret;
}
void dfs1(int u,int fath,int depth)
{
fa[u]=fath;dep[u]=depth;size[u]=;
for (int i=head[u];i;i=a[i].pre){
int v=a[i].to;
if (v==fath) continue;
dfs1(v,u,depth+);
size[u]+=size[v];
if (size[son[u]]<size[v]) son[u]=v;
}
}
void dfs2(int u,int tp)
{
w[u]=++cntw;top[u]=tp; old[cntw]=u;
if (son[u]!=) dfs2(son[u],tp);
for (int i=head[u];i;i=a[i].pre){
int v=a[i].to;
if (v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
double ans1,ans2;
void query(int u,int v)
{
int f1=top[u],f2=top[v],num=;
double ret_sum=0.0,ret_sqr=0.0;
while (f1!=f2) {
if (dep[f1]<dep[f2]) swap(f1,f2),swap(u,v);
num+=(w[u]-w[f1]+);
ret_sum=ret_sum+query_sum(,w[f1],w[u]);
ret_sqr=ret_sqr+query_sqr(,w[f1],w[u]);
u=fa[f1]; f1=top[u];
}
if (dep[u]>dep[v]) swap(u,v);
num+=(w[v]-w[u]+);
ret_sum=ret_sum+query_sum(,w[u],w[v]);
ret_sqr=ret_sqr+query_sqr(,w[u],w[v]);
ans1=ret_sum/(1.0*num);
ans2=ret_sqr/(1.0*num)-(ans1*ans1);
}
signed main()
{
freopen("lemontree.in","r",stdin);
freopen("lemontree.out","w",stdout);
n=read();
for (int i=;i<=n;i++){
int u=read(),v=read();
adde(u,v); adde(v,u);
}
dfs1(,,);
dfs2(,);
for (int i=;i<=n;i++) scanf("%lf",&tmp[i]);
for (int i=;i<=n;i++) val[i]=tmp[old[i]];
build(,,n);
int op; double x,y;
while(~scanf("%d%lf%lf",&op,&x,&y)) {
int u,v; double d;
if (op==) {
u=(int)x; d=1.0*y;
modify(,w[u],d);
} else if (op==) {
u=(int)x; d=(double)y;
update(,w[u],w[u]+size[u]-,d);
} else if (op==) {
u=(int)x; v=(int)y;
query(u,v);
printf("%.5lf\n",ans1);
} else if (op==) {
u=(int)x;v=(int)y;
if (u==v) { puts("0.000"); continue;}
query(u,v);
printf("%.5lf\n",ans2);
}
}
return ;
}
lemontree.cpp
考试时hjc得分最高拿到44分，原因是使用的cin，读入被卡了
关于cin他已经死了...
剩下的人全部打了2分的部分分什么情况(dfs都不会了么...)
题意概括：
对于第一问50pts询问一个序列的所有子序列bit-and和bit-or 的和各是多少。
对于第二问50pts询问n个盒子里装有奖品，m个人等概率随机 选择奖品，选完之后空盒子放回,求奖品剩余数期望。
Sol：
第一小问：求按位and连续子序列和
对于位运算的题目按位考虑，对于每一位，只有连续为1的区间对 答案产生贡献。
假设第k位上某段连续区间长为len，那么贡献值是$ \frac{len\times (len+1)}{2} \times 2 ^k $ 累加所有位的贡献即可。
第二小问：求按位or连续子序列和
只有连续为0的区间对答案产生负贡献，
假设第k位上某段连续区间长为len，
那么贡献值是$ −\frac{len\times (len+1)}{ 2} \times 2 ^k $
补集转换即可。
总复杂度$ O(n log_2 n) $
对于第二个问题直接推公式，
对于每个奖品不被选中的概率是$\frac{n-1}{n}$
所以对于m个人都没选这个奖品的概率是$(\frac{n-1}{n})^m$
所以剩余奖品的期望是$n\times (\frac{n-1}{n})^m $
是在mod p=998244353意义下运算，所以直接求逆元
$ (n-1)^m \times (n^{-1})^m \times n $
对于指数部分直接扩展欧拉定理降幂即可，对于大整数求逆部分考虑性质
若a关于b同余那么a，b必然有相同的逆元。
证明如下： 设$a \equiv b (mod p)$ 那么必然 $ac\equiv bc (mod p)$
若c是a的逆元那么$ac \equiv 1 (mod p )$那么必然$bc \equiv 1 (mod p )$
由逆元的唯一性可证。（事实上可以通过费马小定理求逆元感性理解）
所以根本不需使用高精度复杂度$O(length + 2 log_2 p)$
# include <cstdio>
# include <iostream>
# define int long long
using namespace std;
const int mp=;
const int N=5e5+;
int res1,res2,pw[];
inline void read(int Mo,int Phi)
{
int x=,X=,f=; char c=;
while (!(c>=''&&c<='')) c=getchar();
while (c>=''&&c<='') {
x=(x<<)+(x<<)+c-'';if (x>=Phi)f=; x%=Phi;
X=(X<<)+(X<<)+c-'';X%=Mo;
c=getchar();
}
res1=X,res2=x+(f==?Phi:);
}
inline int Read()
{
int X=,w=; char c=;
while(c<''||c>'') {w|=c=='-';c=getchar();}
while(c>=''&&c<='') X=(X<<)+(X<<)+(c^),c=getchar();
return w?-X:X;
}
int a[N],n;
int workA()
{
int ans=;
for (int i=;~i;i--) {
int ret=;
for (int j=;j<=n;j++)
if ((a[j]>>i)&) ret++;
else {
ans=(ans+ret*(+ret)/%mp*pw[i]%mp)%mp;
ret=;
}
ans=(ans+ret*(+ret)/%mp*pw[i]%mp)%mp;
}
return ans%mp;
}
int workB()
{
int ans=;
for (int i=;~i;i--) {
int ret=; ans=(ans+n*(+n)/%mp*pw[i]%mp)%mp;
for (int j=;j<=n;j++)
if ((a[j]>>i)&) {
ans=((ans%mp-(ret*(+ret)/%mp*pw[i]%mp))%mp+mp)%mp;
ret=;
}else ret++;
ans=((ans%mp-(ret*(+ret)/%mp*pw[i]%mp))%mp+mp)%mp;
}
return ans%mp;
}
int Pow(int x,int n,int p)
{
int ans=;
for (;n;n>>=,x=x*x%p)
if (n&) ans=ans*x%p;
return ans%p;
}
int work2()
{
read(mp,mp-);
int n0=res1,n1=(n0+mp-)%mp,inv_n=Pow(n0,mp-,mp);
read(mp,mp-);
int m=res2;
int ans=Pow(n1,m,mp)*Pow(inv_n,m,mp)%mp*n0%mp;
return ans;
}
signed main()
{
freopen("future.in","r",stdin);
freopen("future.out","w",stdout);
n=Read();
pw[]=;
for (int i=;i<=;i++) pw[i]=pw[i-]*%mp;
for (int i=;i<=n;i++) a[i]=Read();
cout<<workA()<<' '<<workB()<<'\n'<<work2()<<'\n';
return ;
}
future.cpp
最后，考场的评测结果大概是长这样子的。。。
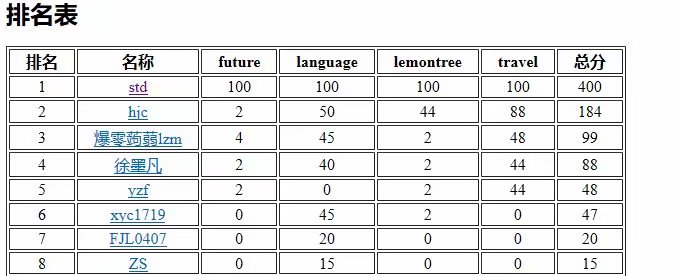
Hjc最巨了!!!
HGOI 20190407 Typing Competition Round #1 出题记的更多相关文章
- Google kickstart 2022 Round A题解
Speed Typing 题意概述 给出两个字符串I和P,问能否通过删除P中若干个字符得到I?如果能的话,需要删除字符的个数是多少? 数据规模 \[1≤|I|,|P|≤10^5 \] 双指针 设置两个 ...
- 对抗密码破解 —— Web 前端慢 Hash
(更新:https://www.cnblogs.com/index-html/p/frontend_kdf.html ) 0x00 前言 天下武功,唯快不破.但在密码学中则不同.算法越快,越容易破. ...
- Scala 的确棒
我的确认为计算机学院应该开一门 Scala 的语言课程. 在这篇文章中,我会讲述为什么我会有这样的想法,在此之前,有几点我想要先声明一下: 本文无意对编程语言进行评比,我要讲述的主体是为什么你应该学习 ...
- GJM : 使用浏览器的计算力，对抗密码破解 [转载]
感谢您的阅读.喜欢的.有用的就请大哥大嫂们高抬贵手"推荐一下"吧!你的精神支持是博主强大的写作动力以及转载收藏动力.欢迎转载! 版权声明:本文原创发表于 [请点击连接前往] ,未经 ...
- mysql datetime查询异常
mysql datetime查询异常 异常:Value '0000-00-00 00:00:00' can not be represented as java.sql.Timestamp (2011 ...
- 51nod 1126 求递推序列的第N项 思路：递推模拟，求循环节。详细注释
题目: 看起来比较难,范围10^9 O(n)都过不了,但是仅仅是看起来.(虽然我WA了7次 TLE了3次,被自己蠢哭) 我们观察到 0 <= f[i] <= 6 就简单了,就像小学初中学的 ...
- 对抗明文口令泄露 —— Web 前端慢 Hash
(更新:https://www.cnblogs.com/index-html/p/frontend_kdf.html ) 0x00 前言 天下武功,唯快不破.但在密码学中则不同.算法越快,越容易破. ...
- Python第七天 函数 函数参数 函数里的变量 函数返回值 多类型传值 函数递归调用 匿名函数 内置函数
Python第七天 函数 函数参数 函数里的变量 函数返回值 多类型传值 函数递归调用 匿名函数 内置函数 目录 Pycharm使用技巧(转载) Python第一天 ...
- 为什么你需要少看垃圾博客以及如何在Python里精确地四舍五入
今天又有一个Python初学者被中文技术博客中的垃圾文章给误导了. 这位初学者的问题是: 在Python中,如何精确地进行浮点数的四舍五入,保留两位小数? 如果你在Google或者百度上搜索,你会发现 ...
随机推荐
- 【学习总结】GirlsInAI ML-diary day-4：变量/Variable
[学习总结]GirlsInAI ML-diary 总 原博github链接-day4 变量/Variable 变量是计算机编程中一个很基础的概念,在计算机程序中,variables are reser ...
- python生成个性二维码学习笔记
在linux环境下进行编码 1.先进家目录,自行创建Code文件夹 cd Code 2.下载MyQR库 sudo pip3 install MyQR 3.下载所需资源文件并解压 Code/ $ wge ...
- 使用PL/SQL连接Oracle时报错ORA-12541: TNS: 无监听程序
因公司需求,安装oracle数据库,oracle数据库用账号密码可以登录,然后在pl/sql里面不能登录,显示无监听程序. 这就说明可能有些服务没有启动,开始运行services.msc ,进入后寻找 ...
- [转帖]震惊，用了这么多年的 CPU 利用率，其实是错的
震惊,用了这么多年的 CPU 利用率,其实是错的 2018年12月22日 08:43:09 Linuxer_ 阅读数:50 https://blog.csdn.net/juS3Ve/article/d ...
- MySQL5.5 安装配置方法教程
MySQL下载地址:http://dev.mysql.com/downloads/installer/ 1.首先进入的是安装引导界面 2.然后进入的是类型选择界面,这里有3个类型:Typical(典型 ...
- python爬虫之git的使用（github的使用）
上面博文中我们简单的了解了一下基本的git操作,但是我们都是将代码放到了本地的仓库里面,但是如果我们是一个团队开发的话,肯定不会放到每个人的本地,必须得有个统一的地方存放代码,国外的大家都在使用git ...
- elasticsearch概念及倒排索引简单介绍
一.概念 集群:一个或者多个节点组织在一起 节点:一个节点是集群中的一个服务器,由一个名字来标识,默认是一个随机的漫威角色名字. 分片:将索引划分为多份的能力,允许水平分割和扩展容量,多个分片相应请求 ...
- mktemp -t -d用法
mktemp命令用于建立暂存文件或者文件夹,帮助文档如下: Usage: mktemp [OPTION]... [TEMPLATE] Create a temporary file or direct ...
- com.alibaba的fastjson简介
fastjson简介 Fastjson是一个Java语言编写的高性能功能完善的JSON库.它采用一种“假定有序快速匹配”的算法,把JSON Parse的性能提升到极致,是目前Java语言中最快的JSO ...
- Yii2的save()方法容易出错的地方
如果save()返回true, 但是数据没有保存成功,则应该是开启了事务且已经回滚 如果save()返回false, 则使用$model->errors查看错误原因 可以设置$model的场景, ...